MATLAB中islocalmin函数用法

目录

语法

说明

示例

向量中的局部最小值

矩阵行中的最小值

相隔最小值

最小值平台区

突出最小值

---

        islocalmin函数的功能是计算局部最小值。

语法

TF = islocalmin(A)
TF = islocalmin(A,dim)
TF = islocalmin(___,Name,Value)
[TF,P] = islocalmin(___)

说明

        ​当在 A 的对应元素中检测到局部最小值时，TF = islocalmin(A) 将返回元素为 1 (true) 的逻辑数组。​
        TF = islocalmin(A,dim) 指定要沿其进行运算的 A 的维度。例如，islocalmin(A,2) 求矩阵 A 中每行的局部最小值。

        TF = islocalmin(___,Name,Value) 支持上述语法中的任何输入参数组合，且可使用一个或多个名称-值参数指定其他用于求局部最小值的参数。例如，islocalmin(A,'SamplePoints',t) 计算 A 相对于时间向量 t 中包含的时间戳的局部最小值。​

        ​[TF,P] = islocalmin(___) 还返回与 A 的每个元素对应的相对高差。​

示例

向量中的局部最小值

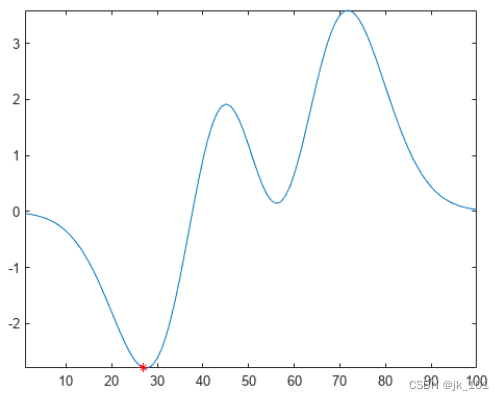
        计算并绘制数据向量的局部最小值。

x = 1:100;
A = (1-cos(2*pi*0.01*x)).*sin(2*pi*0.15*x);
TF = islocalmin(A);
plot(x,A,x(TF),A(TF),'r*')

如图所示：

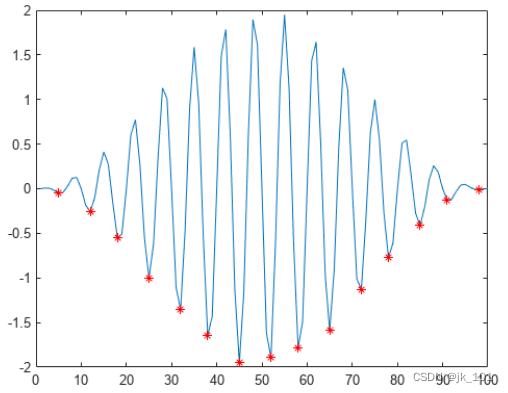
矩阵行中的最小值

        创建一个数据矩阵，然后计算每一行的局部最小值。

A = -25*diag(ones(5,1)) + rand(5,5);
TF = islocalmin(A,2)
TF = 5x5 logical array
 
   0   0   0   1   0
   0   1   0   0   0
   0   0   1   0   0
   0   0   0   1   0
   0   0   1   0   0

相隔最小值

        计算数据向量相对于向量 t 中的时间戳的局部最小值。使用 MinSeparation 参数计算相隔至少 45 分钟的最小值。

t = hours(linspace(0,3,15));
A = [2 4 6 4 3 7 5 6 5 10 4 -1 -3 -2 0];
TF = islocalmin(A,'MinSeparation',minutes(45),'SamplePoints',t);
plot(t,A,t(TF),A(TF),'r*')

如图所示：

最小值平台区

指定用于指示连续最小值的方法。

计算包含连续最小值的数据的局部最小值。指示每个平台区的第一个最小值。

x = 0:0.1:5;
A = max(-0.75, sin(pi*x));
TF1 = islocalmin(A,'FlatSelection','first');
plot(x,A,x(TF1),A(TF1),'r*')

如图所示：

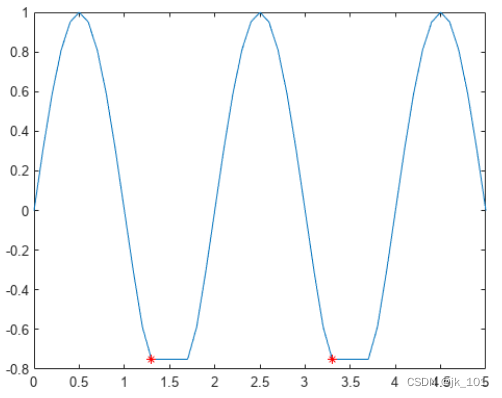
指示每个平台区的所有最小值。

TF2 = islocalmin(A,'FlatSelection','all');
plot(x,A,x(TF2),A(TF2),'r*')

如图所示：

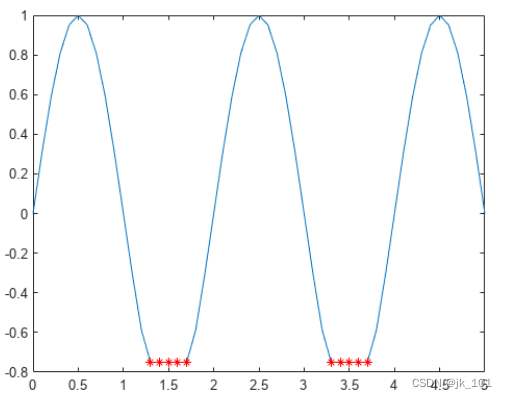
突出最小值

计算数据向量的局部最小值和相对高差，然后用数据绘图。

x = 1:100;
A = peaks(100);
A = A(50,:);
[TF1,P] = islocalmin(A);
 
P(TF1)
ans = 1×2
 
    2.7585    1.7703
 
 
plot(x,A,x(TF1),A(TF1),'r*')
axis tight

如图所示：

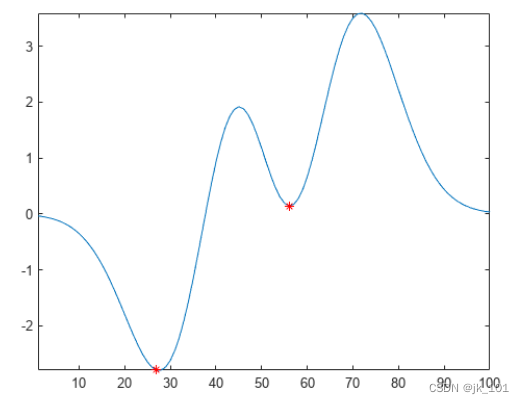
通过指定最小相对高差要求，计算数据中最突出的最小值。

TF2 = islocalmin(A,'MinProminence',2);
plot(x,A,x(TF2),A(TF2),'r*')
axis tight

如图所示：

参数说明

A--输入数据，指定为向量、矩阵、多维数组、表或时间表。

dim--运算维度

        运算维度，指定为正整数标量。如果未指定值，则默认值是大小不等于 1 的第一个数组维度。

以一个 m×n 输入矩阵 A 为例：

• islocalmin(A,1) 根据 A 的每列中的数据计算局部最小值，并返回一个 m×n 矩阵。

  

• islocalmin(A,2) 根据 A 的每行中的数据计算局部最小值，并返回一个 m×n 矩阵。

  

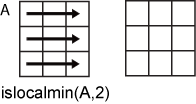
        对于表或时间表输入数据，不支持 dim，并且分别对每个表或时间表变量进行运算。

局部最小值的相对高差

        局部最小值（或波谷）的相对高差根据该波谷相对其他波谷的深度和位置衡量其突出程度。

        要测量一个波谷的相对高差，首先从该波谷延伸一条水平线。找出这条直线与左右两侧数据的交点，交点应为另一波谷或数据的端点。将这些位置标记为左右区间的外部端点。然后找出左右区间内的最高波峰。取这两个波峰的较小值，测量从该波峰到波谷的垂直距离。此距离就是相对高差。

        对于向量 x，最大相对高差不超过 max(x)-min(x)。