代码随想录算法训练营第49天|121. 买卖股票的最佳时机，买卖股票的最佳时机II

链接: 121. 买卖股票的最佳时机
链接: 122.买卖股票的最佳时机II

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

这道题得解题关键时，需要一个二维数组用两列来表示不同状态下（持有，不持有），每天所获得最大利润。

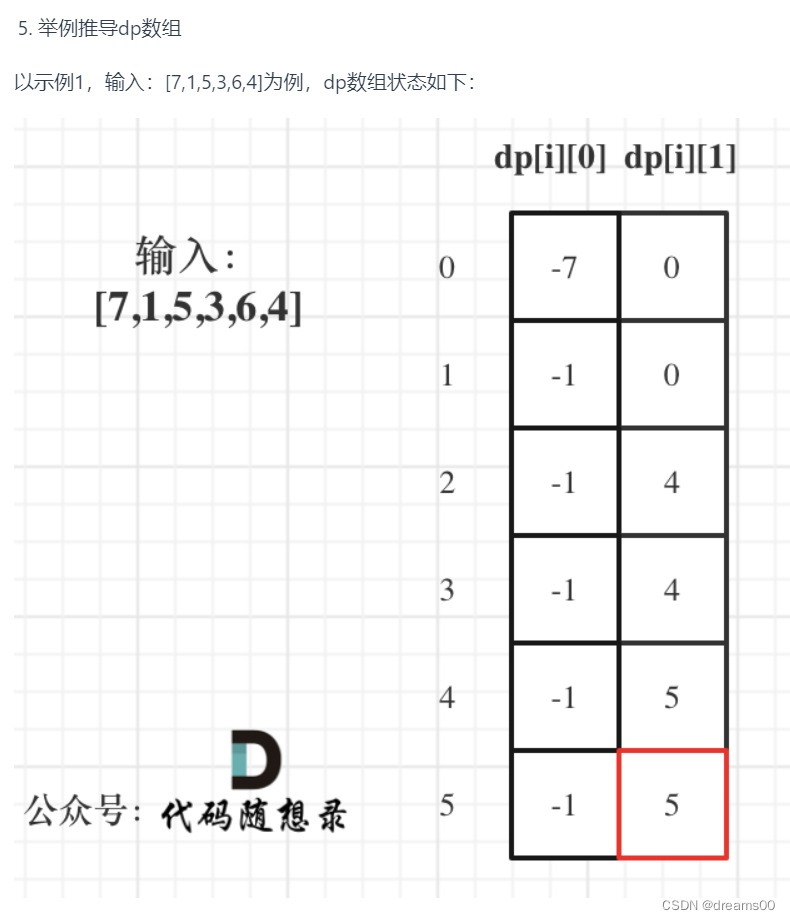
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        /**
          dp[i][0] 表示第i天持有该股票所获得最大利润
          dp[i][1] 表示第i天不持有该股票所获得最大利润
         */
        dp[0][0] = -prices[0];
        dp[0][1] = 0;

        for(int i = 1; i < prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
        }

        return dp[prices.length - 1][1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

买卖股票的最佳时机II

这里重申一下dp数组的含义：

• dp[i][0] 表示第i天持有股票所得现金。
• dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]，那么可以由两个状态推出来

• 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
• 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

在121. 买卖股票的最佳时机 (opens new window)中，因为股票全程只能买卖一次，所以如果买入股票，那么第i天持有股票即dp[i][0]一定就是 -prices[i]。

而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。

那么第i天持有股票即dp[i][0]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即：dp[i - 1][1] - prices[i]。

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        int[][] dp = new int[len][2];

        dp[0][0] = -prices[0];
        dp[0][1] = 0;

        for(int i = 1; i < prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
        }

        return dp[len-1][1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16