线性代数的本质(一)——向量空间

《线性代数的本质》 - 3blue1brown
高中数学A版选修4-2 矩阵与变换
《线性代数及其应用》(第五版)
《高等代数简明教程》- 蓝以中

向量空间

In the beginning Grant created the space. And Grant said, Let there be vector: and there was vector.

向量及其性质

三维几何空间中的一个有向线段称为向量(vector)。本文统一用 $a,b,c,k,\lambda$ 表示标量，小写黑体字母 $\mathbf{u},\mathbf{v},\mathbf{w},\mathbf{a},\mathbf{b},\mathbf{x}$ 表示向量。

向量通常定义两种运算：加法和数乘。加法遵循三角形法则(平行四边形法则)，数乘被称为缩放(scaling)。运算法则如下图

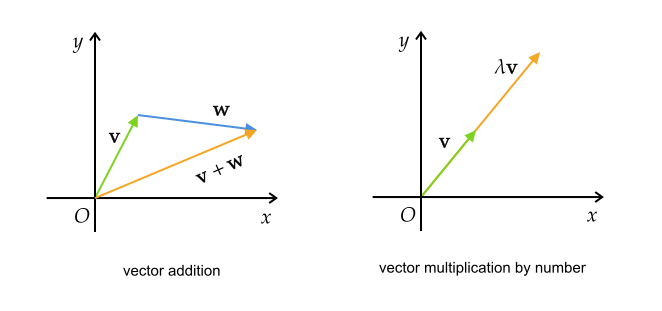
性质：根据向量的几何性质可证明向量的加法和数乘满足以下八条性质：

1. 加法交换律：$\mathbf{v}+\mathbf{w}=\mathbf{w}+\mathbf{v}$
2. 加法结合律：$\mathbf{u}+(\mathbf{v}+\mathbf{w})=(\mathbf{u}+\mathbf{v})+\mathbf{w}$
3. 加法单位元：$\exists 0\in V,0+\mathbf{v}=\mathbf{v}$
4. 加法逆元：$\exists (-\mathbf{v})\in V,\mathbf{v}+(-\mathbf{v})=0$
5. 数乘结合律：$a(b\mathbf{v})=(ab)\mathbf{v}$
6. 数乘分配律：$a(\mathbf{v}+\mathbf{w})=a\mathbf{v}+a\mathbf{w}$
7. 数乘分配律：$(a+b)\mathbf{v}=a\mathbf{v}+b\mathbf{v}$
8. 数乘单位元：$\exists 1\in \mathbb{F},1\mathbf{v}=\mathbf{v}$

向量空间是三维几何空间向高维空间的推广。线性代数中，每个向量都以坐标原点为起点，那么任何一个向量就由其终点唯一确定。从而，向量和空间中的点一一对应。因此，空间也可以看成由所有向量组成的集合，并且集合中的元素可以进行加法和数乘运算。于是，便有了向量空间的抽象定义。

向量空间： 设 $V$ 为 $n$ 维向量的非空集合，$\mathbb{F}$ 是一个数域，若 $V$ 对于向量的加法和数乘两种运算封闭，那么称集合 $V$ 为数域 $F$ 上的向量空间(vector space)。所谓封闭是指

1. $\forall \mathbf{v},\mathbf{w}\in V,\mathbf{v}+\mathbf{w}\in V$
2. $\forall \mathbf{v}\in V,c\in F,c\mathbf{v}\in V$

线性代数中的数域通常取全体实数，即 $\mathbb{F}=\mathbb{R}$。

例如：$n$维向量的全体生成实数域上的向量空间

R n = { x = ( x 1 , x 2 , ⋯   , x n ) ∣ x 1 , x 2 , ⋯   , x n ∈ R } \R^n=\{\mathbf x=(x_1,x_2,\cdots,x_n)\mid x_1,x_2,\cdots,x_n\in\R\} Rn={x=(x1​,x2​,⋯,xn​)∣x1​,x2​,⋯,xn​∈R}

子空间：设 $U$ 是向量空间 $V$ 的一个非空子集，如果$U$中的线性运算封闭，则 $U$ 也是向量空间，称为 $V$ 的子空间。

基与维数

仿照解析几何的基本方法，建立一个坐标系，实现空间内的点与有序实数对一一对应，从而空间内的向量与有序实数对也一一对应，这样就可以用代数方法来研究向量的性质。

为方便建立空间的坐标系，先定义几个概念。

定义：取向量空间 $V$ 内一个向量组 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_r$

1. 向量 $x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\cdots +x_r{\mathbf{a}}_r$ 称为向量组的一个线性组合(linear combination)
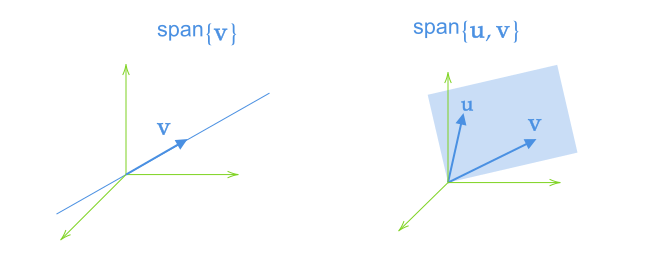
2. 向量组的所有线性组合构成的向量集称为由该向量组张成的空间，记作
   span { a 1 , ⋯   , a n } = { x 1 a 1 + ⋯ + x n a n ∣ x 1 , ⋯   , x n ∈ R } \text{span}\{\mathbf a_1,\cdots,\mathbf a_n\}=\{x_1\mathbf a_1+\cdots+x_n\mathbf a_n\mid x_1,\cdots,x_n\in\R\} span{a1​,⋯,an​}={x1​a1​+⋯+xn​an​∣x1​,⋯,xn​∈R}
   如下图，若 $\mathbf{u},\mathbf{v}\in {\mathbb{R}}^3$ 不共线，则 span { u , v } \text{span}\{\mathbf u,\mathbf v\} span{u,v} 是${\mathbb{R}}^3$中包含 $\mathbf{u},\mathbf{v}$ 和原点的平面，图示

3. 当且仅当系数 $x_1=x_2=\cdots =x_r=0$ 时，线性组合为零
$$x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\cdots +x_r{\mathbf{a}}_r=0$$
则称向量组线性无关(linearly independence)。反之，如果存在不全为零的数使上式成立，则称向量组线性相关(linearly dependence)。

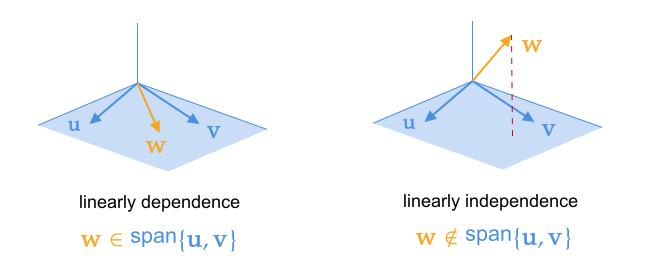
定理：若向量 $\mathbf{v}$ 可由线性无关的向量组${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_r$ 线性表示，则表示系数是唯一的。

证明：设向量$\mathbf{v}$ 有两组表示系数
$$\begin{gathered} \mathbf{b}=k_1{\mathbf{a}}_1+k_2{\mathbf{a}}_2+\cdots +k_r{\mathbf{a}}_r \\ \mathbf{b}=l_1{\mathbf{a}}_1+l_2{\mathbf{a}}_2+\cdots +l_r{\mathbf{a}}_r \end{gathered}$$
则有
$$(k_1-l_1){\mathbf{a}}_1+(k_1-l_2){\mathbf{a}}_2+\cdots +(k_1-l_r){\mathbf{a}}_r=0$$
因为 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_r$ 线性无关，故必有
$$k_1-l_1=k_1-l_1=\cdots =k_1-l_1=0$$
即表示系数是唯一的。

接下来，我们自然想用一组线性无关的向量来张成整个向量空间。

向量空间的基：张成向量空间$V$的一个线性无关的向量集合称为该空间的一组基(basis)。基向量组所含向量的个数，称为向量空间 $V$的维数(dimension)，记为 $\dim V$。

可以证明，向量空间的任意一组基的向量个数是相等的。
单由零向量组成的向量空间 { 0 } \{0\} {0}称为零空间。零空间的维数定义为零。

基定理：$n$ 维向量空间的任意 $n$ 个线性无关的向量构成空间的一组基。

向量的坐标运算

向量空间选定了基向量后，空间中全体向量的集合与全体有序实数组的集合之间就建立了一一 对应的关系。

坐标：设向量组 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n$ 是线性空间 $V$ 的一组基，则空间内任一向量 $\mathbf{v}\in V$ 都可表示为基向量的唯一线性组合
$$\mathbf{v}=x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\cdots +x_n{\mathbf{a}}_n$$
有序数组 $x_1,x_2,\cdots ,x_n$ 称为向量$\mathbf{v}$ 在基 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n$ 下的坐标，一般记作
[ x 1 x 2 ⋮ x n ] or ( x 1 , x 2 , ⋯   , x n ) [x1x2⋮xn]

\quad \text{or}\quad (x_1,x_2,\cdots,x_n) ​x1​x2​⋮xn​​ ​or(x1​,x2​,⋯,xn​)
类似于三维几何空间，由$n$个有序数构成的向量称为$n$维向量。

例：设 v 1 = [ 3 6 2 ] , v 2 = [ − 1 0 1 ] , x = [ 3 12 7 ] \mathbf v_1=[362]

,\mathbf v_2=[−101],\mathbf x=[3127] v1​= ​362​ ​,v2​= ​−101​ ​,x= ​3127​ ​ 。判断 $\mathbf{x}$ 是否在 H = span  { v 1 , v 2 } H=\text{span }\{\mathbf v_1,\mathbf v_2\} H=span {v1​,v2​} 中，如果是，求 $\mathbf{x}$ 相对于基向量 B = { v 1 , v 2 } B=\{\mathbf v_1,\mathbf v_2\} B={v1​,v2​} 的坐标。

解：如果 $\mathbf{x}$ 在 H = span  { v 1 , v 2 } H=\text{span }\{\mathbf v_1,\mathbf v_2\} H=span {v1​,v2​} 中，则下列方程是有解的
c 1 [ 3 6 2 ] + c 2 [ − 1 0 1 ] = [ 3 12 7 ] c_1[362]

+c_2[−101]=[3127] c1​ ​362​ ​+c2​ ​−101​ ​= ​3127​ ​
如果数 $c_1,c_2$存在，则它们是 $\mathbf{x}$ 相对于$B$ 的坐标。由初等行变换得
$$\left[\begin{array}{c}\begin{array}{ccc}3& -1& 3\\ 6& 0& 12\\ 2& 1& 7\end{array}\end{array}\right]\to \left[\begin{array}{c}\begin{array}{ccc}1& 0& 2\\ 0& 1& 3\\ 0& 0& 0\end{array}\end{array}\right]$$
于是， $\mathbf{x}$ 相对于${\mathbf{v}}_1,{\mathbf{v}}_2$ 的坐标
$${\mathbf{v}}_B=\left[\begin{array}{c}3\\ 2\end{array}\right]$$

有时为了区分坐标的基向量，向量 $\mathbf{v}$ 在基 B = { b 1 , b 2 , ⋯   , b n } B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\} B={b1​,b2​,⋯,bn​} 下的坐标，记作 ${\mathbf{v}}_B$

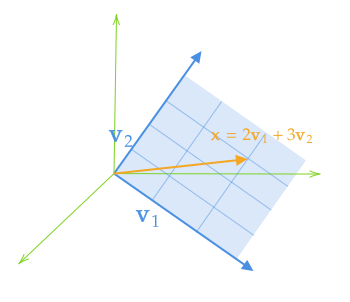
建立了坐标之后，$V$中抽象的向量 $\mathbf{v}$ 和${\mathbb{R}}^n$中具体的数组 $(x_1,x_2,\cdots ,x_n{)}^T$ 实现了一一对应，并且向量的线性运算也可以表示为坐标的线性运算。

设 $\mathbf{v},\mathbf{w}\in V$，有
$$\begin{gathered} \mathbf{v}=v_1{\mathbf{a}}_1+v_2{\mathbf{a}}_2+\cdots +v_n{\mathbf{a}}_n \\ \mathbf{w}=w_1{\mathbf{a}}_1+w_2{\mathbf{a}}_2+\cdots +w_n{\mathbf{a}}_n \end{gathered}$$

向量加法运算
$$\mathbf{v}+\mathbf{w}=(v_1+w_1){\mathbf{a}}_1+(v_2+w_2){\mathbf{a}}_2+\cdots +(v_n+w_n){\mathbf{a}}_n$$
即对应的坐标运算为
[ v 1 v 2 ⋮ v n ] + [ w 1 w 2 ⋮ w n ] = [ v 1 + w 1 v 2 + w 2 ⋮ v n + w n ] [v1v2⋮vn]

+ [w1w2⋮wn]= [v1+w1v2+w2⋮vn+wn] ​v1​v2​⋮vn​​ ​+ ​w1​w2​⋮wn​​ ​= ​v1​+w1​v2​+w2​⋮vn​+wn​​ ​

向量数乘运算
$$c\mathbf{v}=(c{v}_1){\mathbf{a}}_1+(c{v}_2){\mathbf{a}}_2+\cdots +(c{v}_n){\mathbf{a}}_n$$
即对应的坐标运算为
c [ v 1 v 2 ⋮ v n ] = [ c v 1 c v 2 ⋮ c v n ] c[v1v2⋮vn]

= [cv1cv2⋮cvn] c ​v1​v2​⋮vn​​ ​= ​cv1​cv2​⋮cvn​​ ​

向量的坐标取值依托于坐标系的基向量。选取的基向量不同，其所对应的坐标值就不同。当然，基向量自身的坐标总是：

e 1 = [ 1 0 ⋮ 0 ] , e 2 = [ 0 1 ⋮ 0 ] , ⋯   , e n = [ 0 0 ⋮ 1 ] , \mathbf e_1=[10⋮0]

,\quad \mathbf e_2=[01⋮0],\quad \cdots,\quad \mathbf e_n=[00⋮1],\quad e1​= ​10⋮0​ ​,e2​= ​01⋮0​ ​,⋯,en​= ​00⋮1​ ​,
这种坐标形式通常称为标准向量组(或单位坐标向量组)。

总之，在$n$维向量空间 $V_n$ 中任取一组基，则 $V_n$ 中的向量与 ${\mathbb{R}}^n$ 中的数组之间就有一一对应的关系，且这个对应关系保持线性组合(线性运算)的一一对应。接下来我们将默认使用标准坐标系：坐标原点为 $O$，基向量组为 ${\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n$ 。后续将对向量实体和坐标不做区分。