竞赛 基于大数据的时间序列股价预测分析与可视化 - lstm

1 前言

🔥 优质竞赛项目系列，今天要分享的是

🚩 毕业设计 大数据时间序列股价预测分析系统

该项目较为新颖，适合作为竞赛课题方向，学长非常推荐！

🥇学长这里给一个题目综合评分(每项满分5分)

• 难度系数：3分
• 工作量：3分
• 创新点：3分

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate

2 时间序列的由来

提到时间序列分析技术，就不得不说到其中的AR/MA/ARMA/ARIMA分析模型。这四种分析方法的共同特点都是跳出变动成分的分析角度，从时间序列本身出发，力求得出前期数据与后期数据的量化关系，从而建立前期数据为自变量，后期数据为因变量的模型，达到预测的目的。来个通俗的比喻，大前天的你、前天的你、昨天的你造就了今天的你。

2.1 四种模型的名称：

• AR模型：自回归模型（Auto Regressive model）；
• MA模型：移动平均模型（Moving Average model）；
• ARMA：自回归移动平均模型（Auto Regressive and Moving Average model）；
• ARIMA模型：差分自回归移动平均模型。
• AR模型：

如果某个时间序列的任意数值可以表示成下面的回归方程，那么该时间序列服从p阶的自回归过程，可以表示为AR§：

AR模型利用前期数值与后期数值的相关关系（自相关），建立包含前期数值和后期数值的回归方程，达到预测的目的，因此成为自回归过程。这里需要解释白噪声，白噪声可以理解成时间序列数值的随机波动，这些随机波动的总和会等于0，例如，某饼干自动化生产线，要求每包饼干为500克，但是生产出来的饼干产品由于随机因素的影响，不可能精确的等于500克，而是会在500克上下波动，这些波动的总和将会等于互相抵消等于0。

3 数据预览

​
import pandas as pd
import matplotlib.pyplot as plt
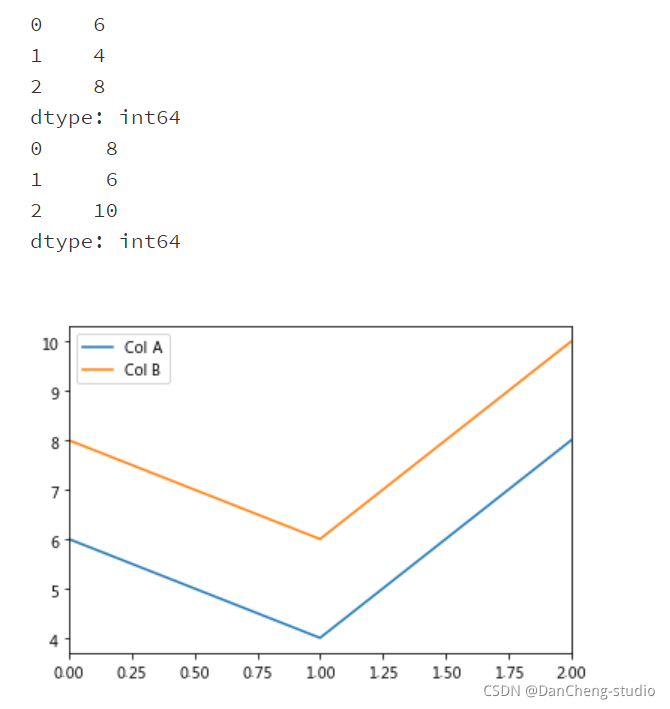
%matplotlib inline

#准备两个数组
list1 = [6,4,8]
list2 = [8,6,10]

#分别将list1，list2转为Series数组
list1_series = pd.Series(list1) 
print(list1_series)
list2_series = pd.Series(list2) 
print(list2_series)

#将两个Series转为DataFrame，对应列名分别为A和B
frame = { 'Col A': list1_series, 'Col B': list2_series } 
result = pd.DataFrame(frame)

result.plot()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

4 理论公式

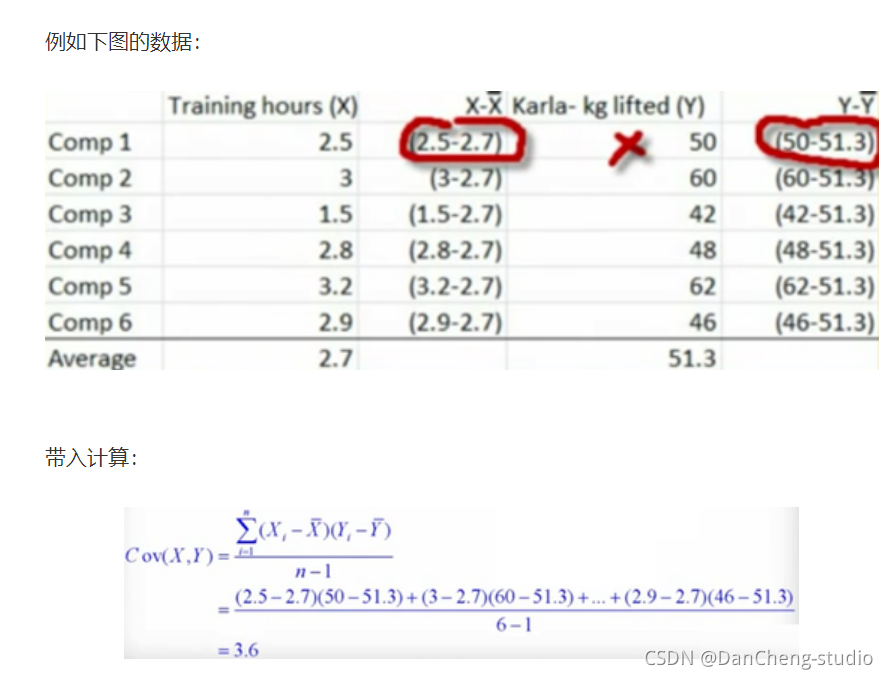
4.1 协方差

首先看下协方差的公式：

4.2 相关系数

计算出Cov后，就可以计算相关系数了，值在-1到1之间，越接近1，说明正相关性越大；越接近-1，则负相关性越大，0为无相关性
公式如下：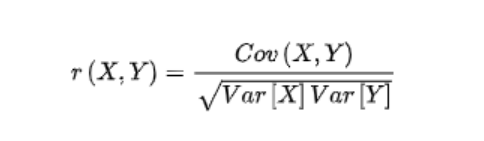

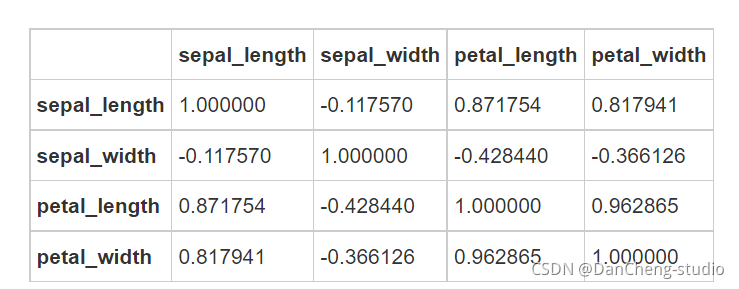
4.3 scikit-learn计算相关性

​
#各特征间关系的矩阵图
sns.pairplot(iris, hue=‘species’, size=3, aspect=1)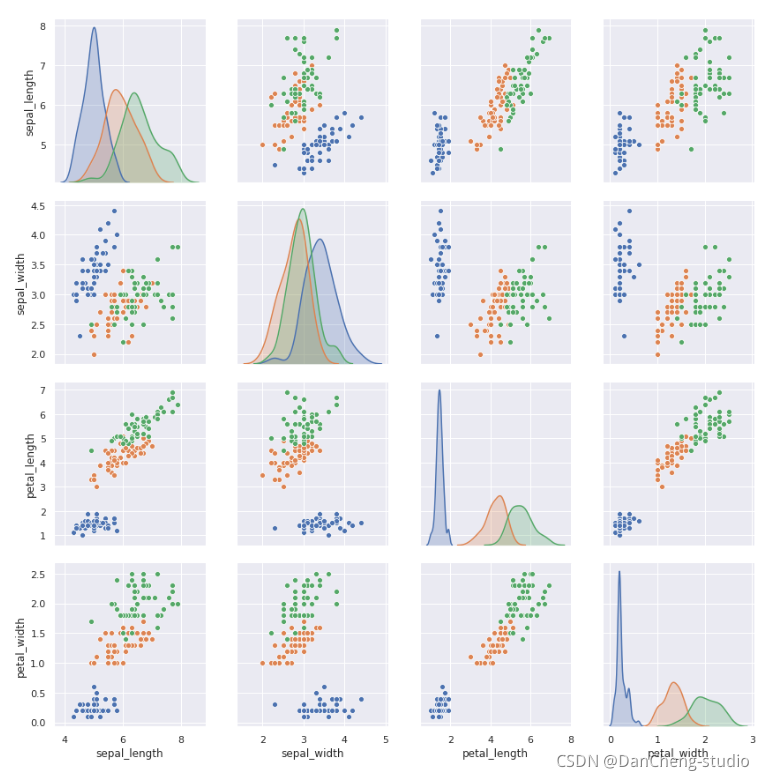

Andrews Curves 是一种通过将每个观察映射到函数来可视化多维数据的方法。
使用 Andrews Curves 将每个多变量观测值转换为曲线并表示傅立叶级数的系数，这对于检测时间序列数据中的异常值很有用。

​
plt.subplots(figsize = (10,8))
pd.plotting.andrews_curves(iris, ‘species’, colormap=‘cool’)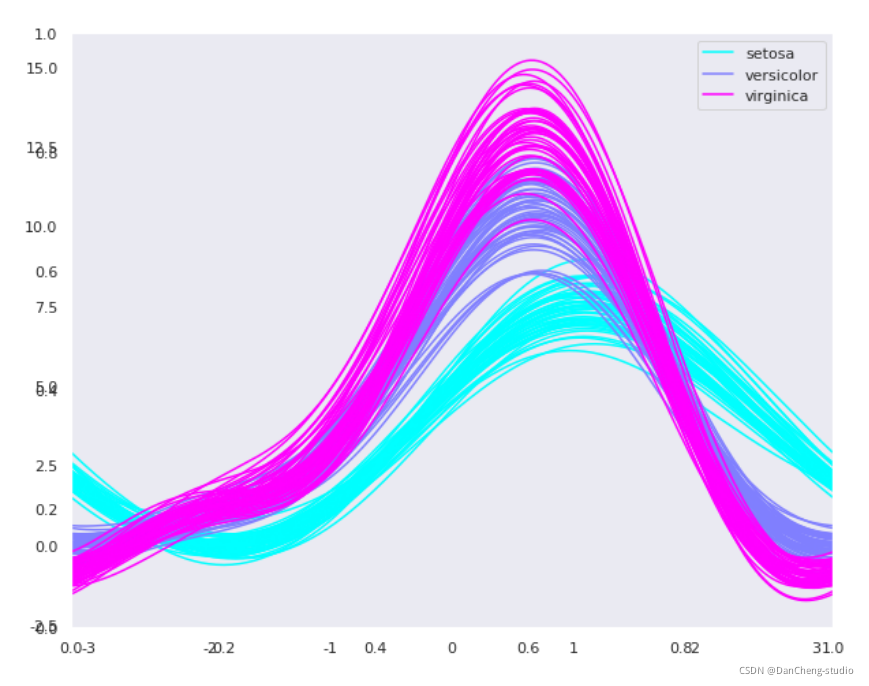

这里以经典的鸢尾花数据集为例

setosa、versicolor、virginica代表了三个品种的鸢尾花。可以看出各个特征间有交集，也有一定的分别规律。

​
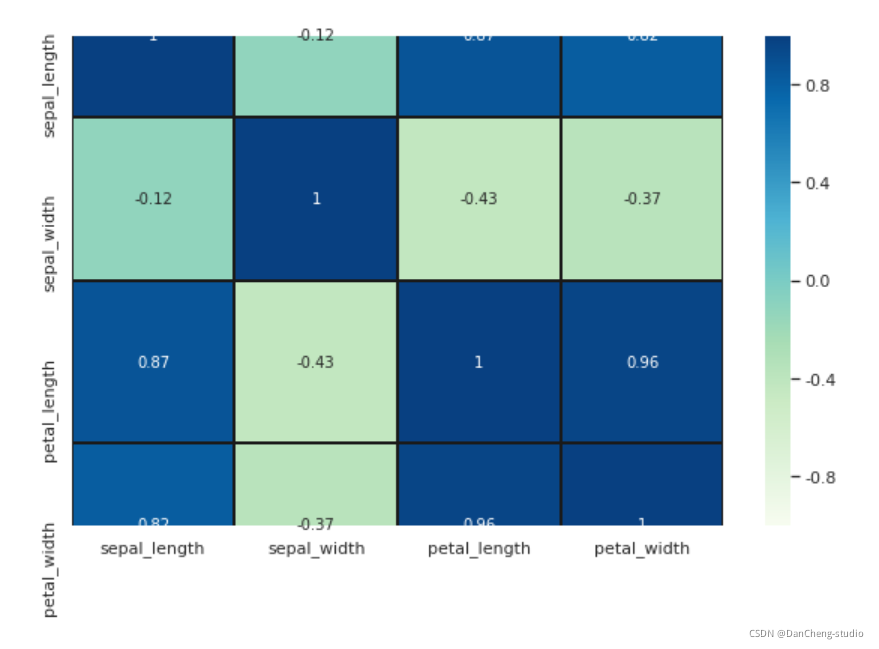
#最后，通过热图找出数据集中不同特征之间的相关性，高正值或负值表明特征具有高度相关性：

fig=plt.gcf()
fig.set_size_inches(10,6)
fig=sns.heatmap(iris.corr(), annot=True, cmap='GnBu', linewidths=1, linecolor='k', \
square=True, mask=False, vmin=-1, vmax=1, \
cbar_kws={"orientation": "vertical"}, cbar=True)
1
2
3
4
5

5 金融数据的时序分析

主要介绍：时间序列变化情况计算、时间序列重采样以及窗口函数

5.1 数据概况

​
import pandas as pd

tm = pd.read_csv('/home/kesci/input/gupiao_us9955/Close.csv')
tm.head()
1
2

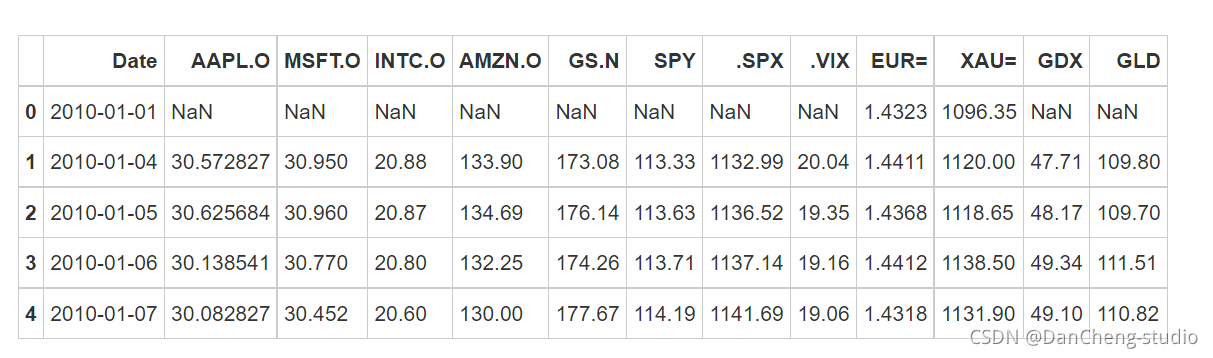
数据中各个指标含义:

• AAPL.O | Apple Stock
• MSFT.O | Microsoft Stock
• INTC.O | Intel Stock
• AMZN.O | Amazon Stock
• GS.N | Goldman Sachs Stock
• SPY | SPDR S&P; 500 ETF Trust
• .SPX | S&P; 500 Index
• .VIX | VIX Volatility Index
• EUR= | EUR/USD Exchange Rate
• XAU= | Gold Price
• GDX | VanEck Vectors Gold Miners ETF
• GLD | SPDR Gold Trust

8年期间价格(或指标)走势一览图

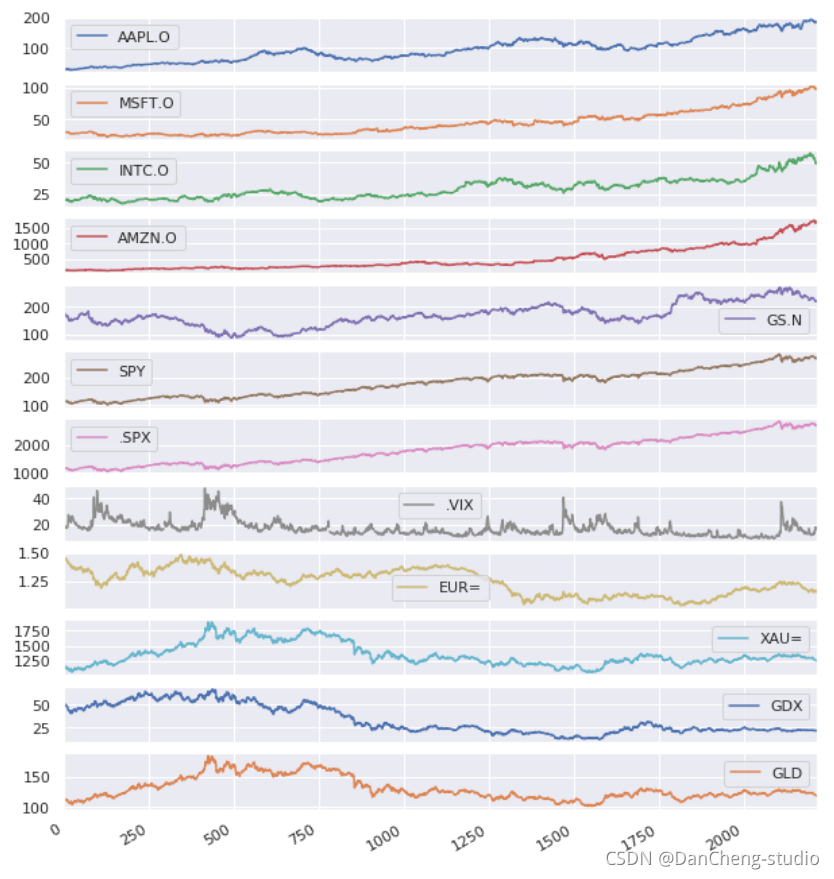
5.2 序列变化情况计算

• 计算每一天各项指标的差异值（后一天减去前一天结果）
• 计算pct_change：增长率也就是 （后一个值-前一个值）／前一个值）
• 计算平均计算pct_change指标
• 绘图观察哪个指标平均增长率最高
• 计算连续时间的增长率（其中需要计算今天价格和昨天价格的差异）

计算每一天各项指标的差异值（后一天减去前一天结果）

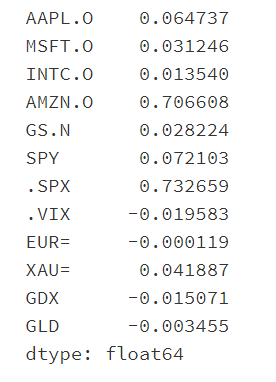
计算pct_change：增长率也就是 （后一个值-前一个值）／前一个值）

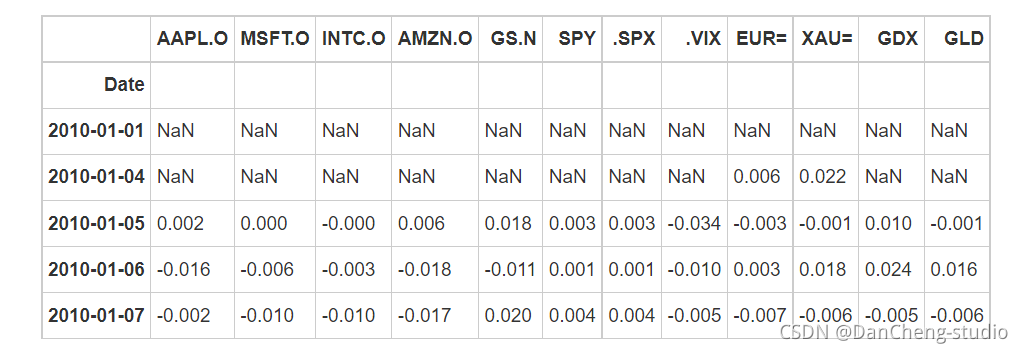
计算平均计算pct_change指标
绘图观察哪个指标平均增长率最高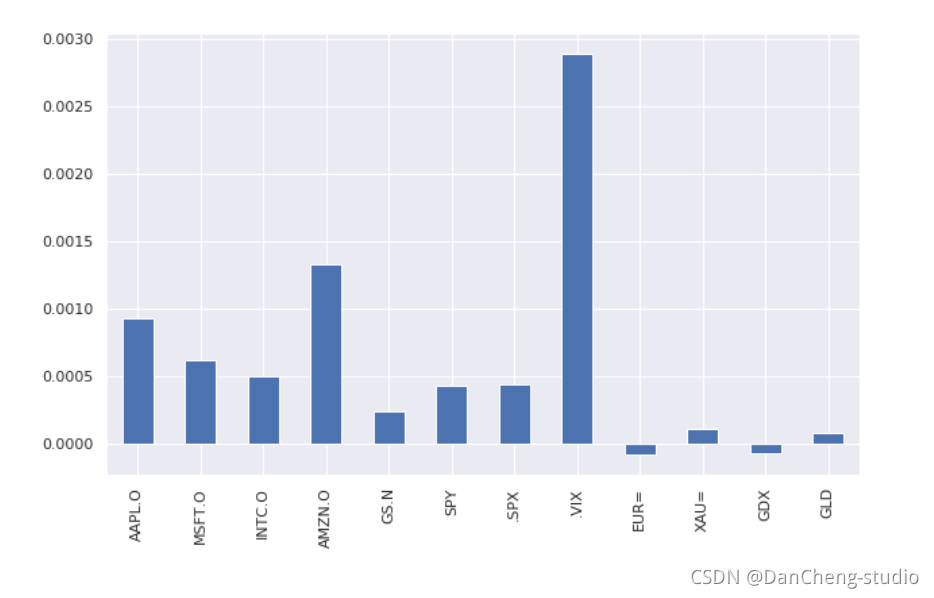

除了波动率指数(.VIX指标)增长率最高外，就是亚马逊的股价了！贝佐斯简直就是宇宙最强光头强

计算连续时间的增长率（其中需要计算今天价格和昨天价格的差异）

​
#第二天数据
tm.shift(1).head()

#计算增长率
rets = np.log(tm/tm.shift(1))
print(rets.tail().round(3))

#cumsum的小栗子：
print('小栗子的结果：',np.cumsum([1,2,3,4]))

#增长率做cumsum需要对log进行还原，用e^x
rets.cumsum().apply(np.exp).plot(figsize=(10,6))
1
2
3
4
5
6
7
8
9

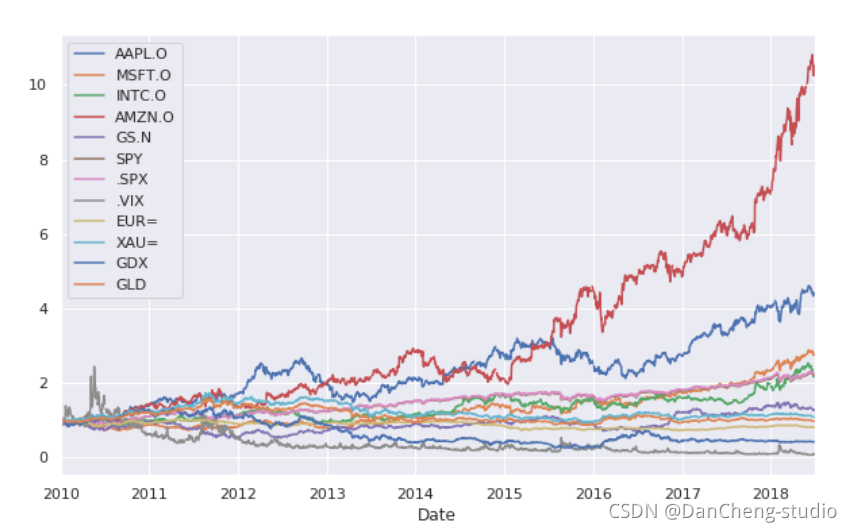
以上是在连续时间内的增长率，也就是说，2010年的1块钱，到2018年已经变为10多块了(以亚马逊为例)

(未完待续，该项目为demo预测部分有同学需要联系学长完成)

最后

🧿 更多资料, 项目分享：

https://gitee.com/dancheng-senior/postgraduate