17-数据结构-查找-（顺序、折半、分块）

        简介：查找，顾名思义，是我们处理数据时常用的操作之一。大概就是我们从表格中去搜索我们想要的东西，这个表格，就是所谓的查找表（存储数据的表）。而我们怎么设计查找，才可以让计算机更快的去找到筛选我们所需要的信息呢，因此，关于怎么设计查找，就有了很多道道了。

        比如，单纯的掰着手指头去算，一个一个查，这是顺序查找；又比如，我知道了一个有序数据的最大最小的下标，我直接每次看这组数据中间的值，就跟数字爆炸一样，1和10，我猜5，猜大了，那我就从6和10中间再说他们的中间值8，这样每次可以省一半的时间，这是折半查找；再者数据特别大，我每次查找要么挨个算，要么每次省一半，所需时间还很长，这时候我们就需要分块查找了，它用的时索引结构。索引，也就相当于书的目录，我们去读一本书想读的内容，首先先去目录去找它在第几章，随后在在那一章的第一页开始往下找。分块查找就是这样的，它显示分成块，每一块的第一个下标为该块在索引表的标记，分块查找的特点就是，索引表中是有序的，但块间无序的。
        

---

目录

一、顺序查找

        1.1简介：

 1.2代码：

        1.3实现

二、折半查找

        2.1简介：

        2.2折半思想代码：

        2.3.折半的判断树

三、分块查找

        3.1简介

---

一、顺序查找

        1.1简介：

顺序查找，一般在线性表中进行查找。查找对象的存储结构适用于顺序表和链表。

线性表的顺序表中，分为有序和无序两种情况。

        哨兵思想：就是在数组的开头第一个位置，或结尾第一个位置，不存放数据，从下标1开始存放，给每次需要对比的数据，放在哨兵位置，即下标0处，与之对比。这样可以避免越界。

        无序的话，则是从头到尾挨个遍历因此时间复杂度为O（n）。

        平均查找长度：

         查找成功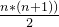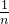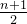： *   =，前面是查找每一个数时的查找次数的总数，是个等差数列，后面乘上每个数被查找的概率，一般都是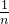,即平分。

        查找失败：就是给数组遍历，遍历到数据的下一位时发现找不到了，所以为n+1即可。

        有序的话，类似于二叉排序树，它可以减少查找失败时的时间，因为有序，当我找的值，遍历到比前一个大，比后一个小时，那么就查找失败了，后面不用再看了。

        平均查找长度：

          查找成功：与无序一样， *   =。

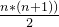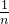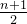           查找失败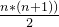：（+n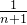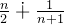）*=,，长方形为不存在的数据范围，查找这些范围，就算失败，后面就不用找了。如图，失败总次数为：1+2+3+3，1+2+3为等差数列，后面再加个3为结尾处无穷的情况。       

 1.2代码：

这里实现了顺序表的顺序查找

主要顺序查找思想：

//查找
int SeqSearch(SSTable* s,int key)
{
	//哨兵处，放进需要对比的值 
	s->data[0]=key;
	
	int i;
	//随后，从表尾进行遍历对比 
	i=s->tabLen;
	//不等于key的时候就一直递减 
	while(s->data[i]!=key)
	{
		i--;
	}
	//如果找到了，则返回i，如果没找到，即最后i=0，跟哨兵坐标相等了，则失败 
	return i;	
}

#include <stdio.h>
#include <string.h>
#include <malloc.h>
//顺序查找结构体
typedef struct 
{
	int *data; //动态一维数组 
	int tabLen;//表长度 
	
}SSTable;//顺序查找表 
//初始化顺序查找表 
void InitSSTable(SSTable *s)
{
	printf("输入表长\n");
	int k;
	scanf("%d",&k);
	s->tabLen=k;
	s->data=(int*)malloc(sizeof(int)*s->tabLen);
}
//查找
int SeqSearch(SSTable* s,int key)
{
	s->data[0]=key;
	
	int i;
	i=s->tabLen;
	while(s->data[i]!=key)
	{
		i--;
	}
	
	return i;	
}
void CreatSSTable(SSTable *s)
{
	printf("表长为%d\n",s->tabLen);
	int i=1;
	printf("请给数组赋值\n");
	while(i<s->tabLen)
	{
		int x;
		scanf("%d",&x);
		s->data[i]=x;	
		i++;
	}
}  
 
int main()
{
	SSTable s;
	InitSSTable(&s);
	CreatSSTable(&s);
	int pos;
	int key;
	printf("请输入要查找的值\n");
	scanf("%d",&key);
	
	pos=BinarySearch(s,key); 
	if(pos!=0)
	printf("%d在表中的下标为%d\n",key,pos);
	else
	printf("表中没有你要找的数据\n");
	
	return 0;
 } 

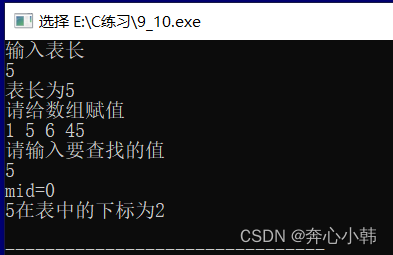
        1.3实现

        

二、折半查找

        2.1简介：

        折半查找，又叫二分查找，它仅适用于有序的顺序表，注意两个特点：1.有序；2.顺序表，进行随机存取操作时。折半字面意思，纸每次对折一半，就跟数字爆炸一样，每次我猜数字都从范围内的中间值猜，猜大猜小，再去另一个区域去猜。

        2.2折半思想代码：

    就是对有序的一维数组，进行折半划分。先定义两个标记遍历。low和high，low在数据最左侧开始，high在数据最右侧，high和low为数组下标，因此high=n-1；数组长度减1.随后进行while循环，循环为low<=high,随后进入循环，开始，先给mid跟新值，mid=（low+high）/2,我们通过mid去看数组中mid处的值，与key对比，如果相等，则返回，如果小于key，说明找的mid偏小了，所以在右区域去找，此时更新low即可，low=mid+1;同理如果大于key，说明大了，更新high=mid-1；

//二分查找
int BinarySearch(SSTable s,int key)
{
	int low=0;
	int high=s.tabLen-1;
	int mid=0;
	while(low <= high)
	{
		printf("mid=%d\n",mid);
		mid=(low+high)/2;
		
		if(s.data[mid]==key)
		return mid;
		else if(s.data[mid]<key)
		{
			low=mid+1;	
		}
		else
			high=mid-1;			
	}
	return 0;	
} 

        2.3.折半的判断树

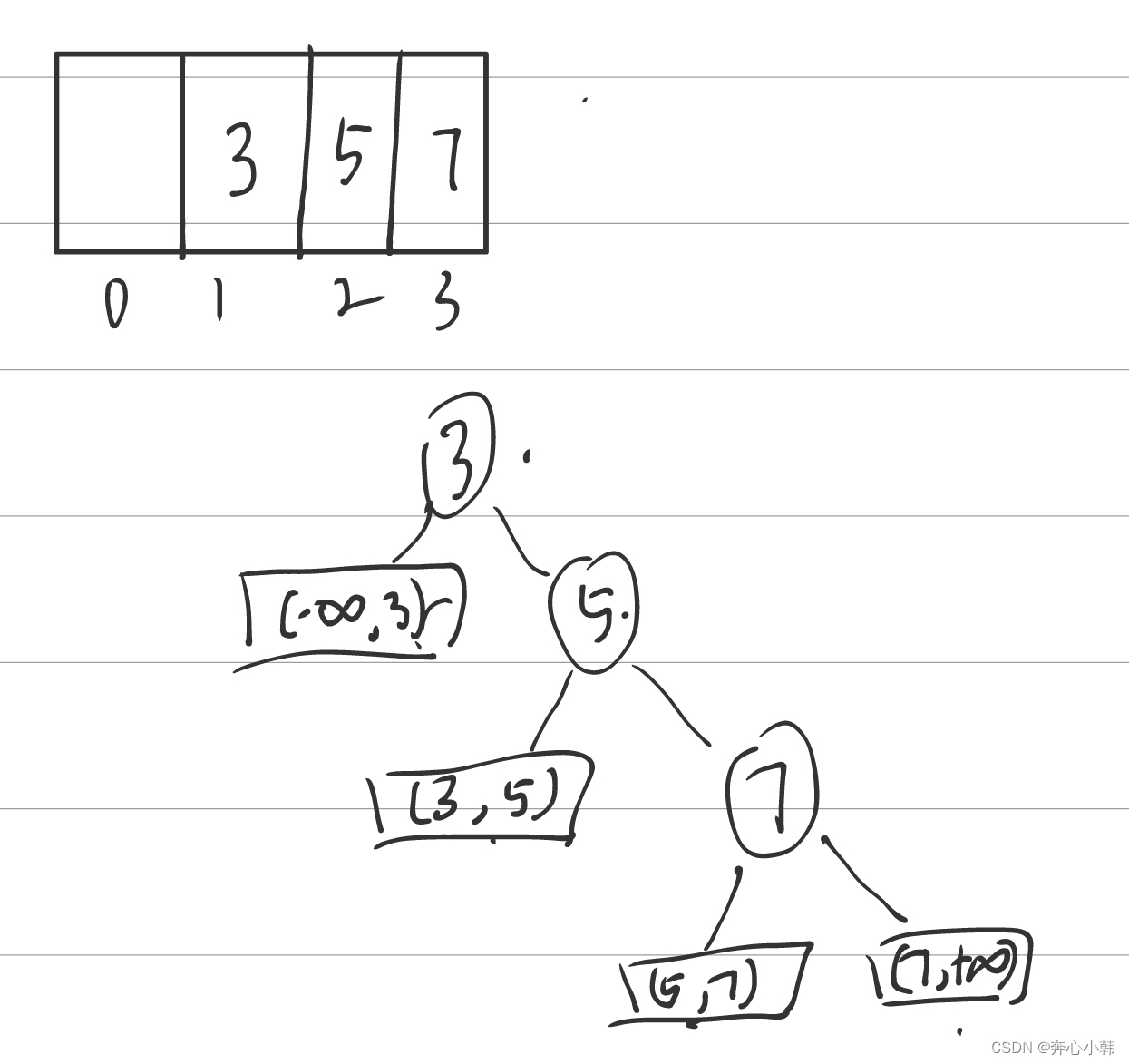
   判断树，顾名思义，就是一个二叉树，通过二分法，去不断化分成两块。每个结点为mid处的值。先后顺序为，先记录low和high的初始值，当low<=high时，随后进行折半查找，先更新mid值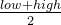,然后看数组mid处的值，与我们查找数对比，大或者小，进行high或low的更新即可。注：每次更新mid时，所得的运算结果，就是代码思想时所得结果，即3/2=1,  5/3=1，只保留整数位，

此外，做题的时候，要看好数据的下标，初始化时low永远都在数据第一个位置的下标处，high在数据最右侧。

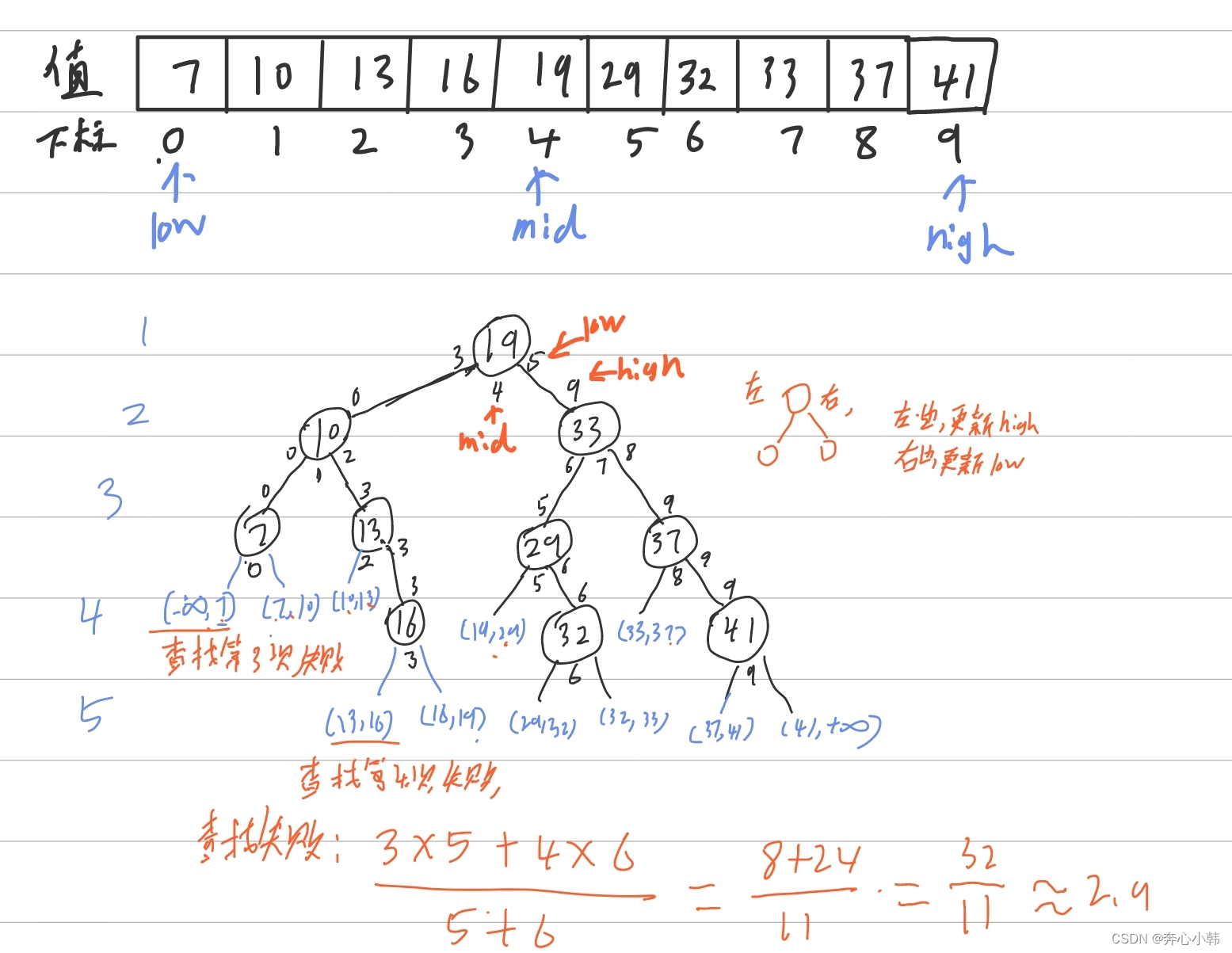
直接上图：

树中，每个结点为数组mid下标处的数值。每次左右更新的时候，更新相应的变量。一个变一个不变。每个结点下面，写一下mid的值，方便计算下一个情况。蓝色区域为失败的区域。

三、分块查找

        3.1简介

        分块查找，仅适用于线性表顺序存储，是对顺序查找和分块查找的优化，它有两个表，一个查找表（正常存储数据的表），一个索引表（给查找表中的数据分成n块，包含该块最大值，和该块其实下标）。分块查找，索引表有序，查找表可以无序，即块内无序，块间有序。

        它用的是索引结构。索引，也就相当于书的目录，我们去读一本书想读的内容，首先先去目录去找它在第几章，随后在在那一章的第一页开始往下找。分块查找就是这样的，它显示分成块，每一块的第一个下标为该块在索引表的标记，分块查找的特点就是，索引表中是有序的，但块间无序的。

        先通过对比索引表中的值，若在在某个块之间，则通过下标，取查找表中遍历即可。

  平均查找长度：

        索引表采用折半查找，查找表采用顺序查找：折半查找相当于树，其树的高度，为平均查找长度不会超过树搞，即log(n)+1即树高的计算公式。顺序查找，则是遍历一遍。即长度为n的表通过划分为b块，每块为a个数据所以n=b*a;

所以总的平均查找为：

log(b)+1+

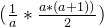
索引表采用折半查找，查找表也采用折半查找：log(b)+1+log(b)+1=log(b)+log(a)+2,其实也就是整个查找表都是有序的，直接对全部进行二分，所以为log(n)+2;

查找效率最高时：即默认n=ba时，b=a=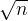时，索引表和查找表都时有序的，都采用二分查找，效率最高。平均查找长度最小。