卷积神经网络（一）

前言

从外行者角度看卷积神经网络会说无非就是卷积层后面跟着一个池化层，但是深入代码实际编写卷积神经网络总是有些困难的。其中包括各种细节比如数据格式、尺寸变化、运算规定等。
参考：

• 1. Zhang A, Lipton ZC, Li M, Smola AJ. Dive into deep learning. arXiv preprint arXiv:210611342. Published online 2021.
• {{Cite book| edition = Di 1 ban| publisher = 机械工业出版社| isbn = 978-7-111-64968-7| last1 = 邱锡鹏著| last2 = 邱锡鹏, author| title = 神经网络与深度学习 = Neural networks and deep learning| location = Beijing| date = 2020}}

卷积层

卷积就是用一个核矩阵对样本的特征矩阵进行卷积，关键要区分什么叫做样本的特征矩阵以及卷积核的尺寸。
对于黑白图像来说，每个样本就是一个黑白图像，用灰度矩阵来表示，假设大小为$[28,28]$，这是一个二维的矩阵，我们需要找一个二维的内核来对他进行卷积。考虑进Padding和Stride也无非就是对样本的特征矩阵周围进行$0$填充并设置相邻两次卷积所相差的横向和纵向的距离。
这里要注意卷积后的尺寸一定是$([(n_h-k_h+p_h)/s_h]+1,[(n_w-k_w+p_w)/s_w]+1)$。
这个尺寸可以通过算几个小的卷积例子来发现。
对于多个样本数据所构成的矩阵我们可以表示为：$(样本数,特征)$，比如100张28*28黑白图片就是：$(100,28,28)$
如果样本的特征是三维结构，比如彩色图像的RGB特征图，那么我们要做的就是用三维核进行卷积。三维数据表示为：$(样本数,特征)$。

多通道

当引入多通道以后，我们就不得不改变上面的数据表示格式。
我们设想一个二维特征数据我们想用不同核来对其进行卷积，那么就会生成多个卷积后的结果，$X@K_1,X@K_2$等等，我们可以把多个核拼在一起计为：$(卷积核数,卷积核)$.
我们可以对于不同的核设置不同的Padding和Stride但是这样会导致特征经过核的卷积后生成的结果尺寸不一致。所以为了数据上的好看，我们把Padding和Stride在不同核之间共享。
然后这样的话我们就会发现一个特殊的事情，原本数据是一个二维数据，但是经过多个核的卷积我们得到了多个二维数据。

那么这个多核卷积后的数据我们可以计为$(卷积核数,卷积后的特征)$，如果把样本数也考虑进来那就是$(样本数,卷积核数,特征)$。
因为我们可能需要多个卷积层连续对数据进行处理，也就是上个卷积层处理完的$(样本数,卷积核数,特征)$我们要让下一个卷积层处理。
我们的卷积肯定还是对特征卷积，也就是卷积核还是二维的，而上一步输出的数据中除了样本数、特征，还多了一维坐标：卷积核数，这个时候下一个卷积层该怎么卷积呢？书中是把这个多出来的坐标当作输入通道数来进行处理，并给出与输入通道数相匹配的多个卷积核来进行一次卷积。
也就是书中所说的每一个输入通道的特征跟对应通道的核进行卷积，然后不同通道卷积的结果相加并加上偏置来作为这个多输入通道的卷积结果。
也就是$(卷积核数(输入通道数),卷积后的特征)$与$(输入通道数,卷积核)$进行卷积累加。而如果我们想再产生几种不同的卷积结果，那么我们就需要对后面的卷积部分加维度，为了便于记忆，我把它成为输出通道数：$(输出通道数,输入通道数,卷积核)$，这样的话我们前面的数据就可以计为：$(样本数,输入通道数,特征)$,卷积核就是：$(输出通道数,输入通道数,卷积核)$，

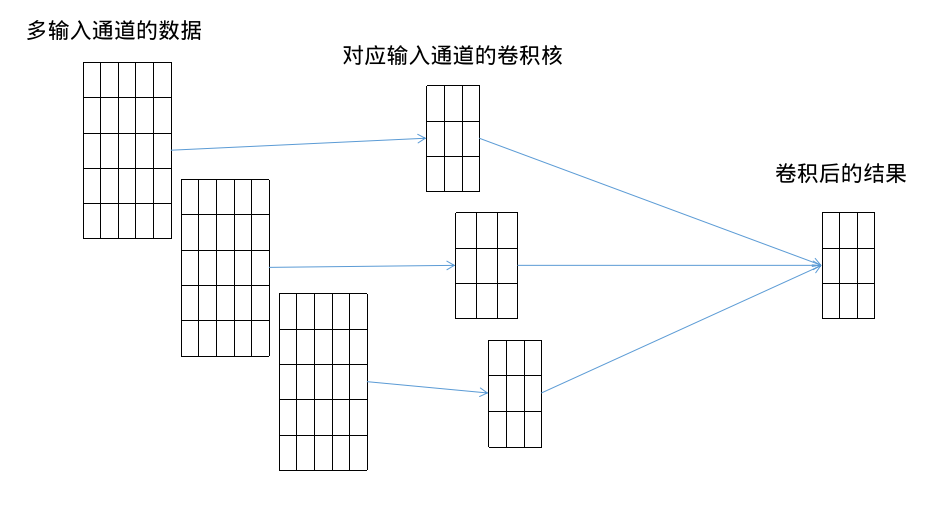
当有多组卷积核的时候：

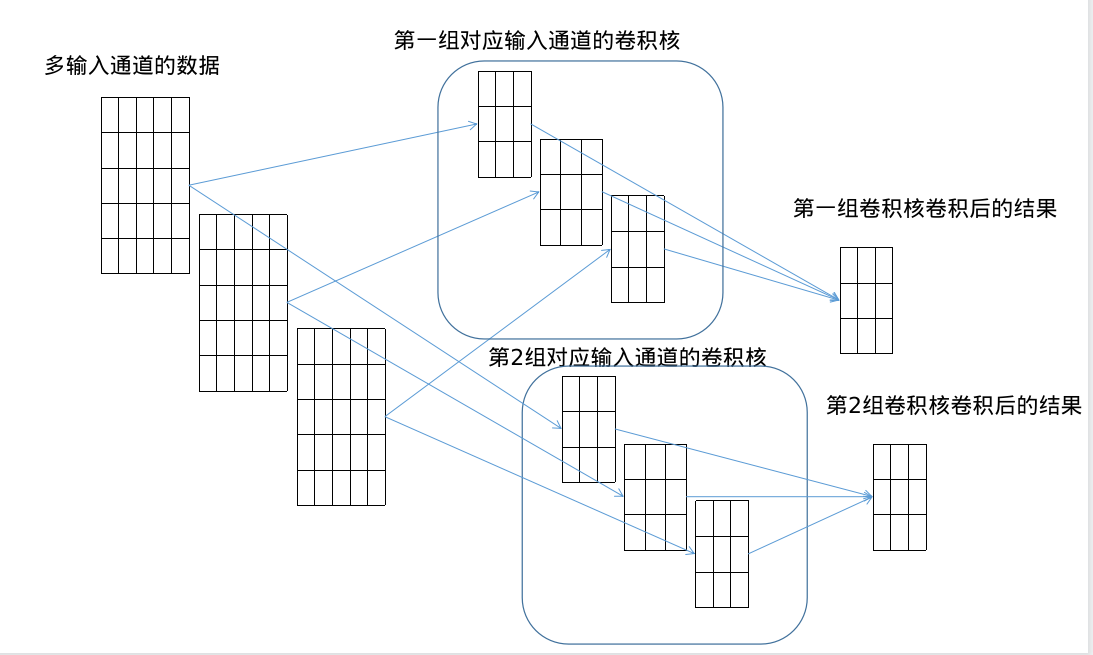
然后我们可以把卷积核标记为：$(输出通道数,输入通道数,卷积核)$,样本数据计为：$(样本数,输入通道数,特征)$，无论对于二维三维都是这样的结构。

池化层

上面我们已经定义了数据的格式，当输入上述数据时，我们的池化层是对每一个特征进行池化的，并不会合并不同通道的特征，所以池化层只需要遍历每个特征并进行同样的池化、Padding、Stride即可。

代码

首先是定义数据的卷积和池化，不涉及输入输出通道

import torch
#二维卷积无padding
def corr2d(Data,Kernel,Stride):
    Y=torch.zeros(((Data.shape[0]-Kernel.shape[0])//(Stride[0])+1,(Data.shape[1]-Kernel.shape[1])//(Stride[1])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j]=(Data[i*Stride[0]:i*Stride[0]+Kernel.shape[0],j*Stride[1]:j*Stride[1]+Kernel.shape[1]]*Kernel).sum()
    return Y
# 测试案例
#corr2d(torch.tensor([[1,2,3],[4,5,6],[5,6,7]]),torch.tensor([[1,2],[2,3]]),Stride=(1,1))
#二维卷积有padding
#def corr2d_pad(Data=(a,b),Kernel=(c,d),Padding=(e,f),Stride=(g,h)):
def corr2d_pad(Data,Kernel,Padding,Stride):
    Data=torch.concatenate((torch.zeros((Padding[0],Data.shape[1])),Data,torch.zeros((Padding[0],Data.shape[1]))),axis=0)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Padding[1])),Data,torch.zeros((Data.shape[0],Padding[1]))),axis=1)
    Y=torch.zeros(((Data.shape[0]-Kernel.shape[0])//(Stride[0])+1,(Data.shape[1]-Kernel.shape[1])//(Stride[1])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j]=(Data[i*Stride[0]:i*Stride[0]+Kernel.shape[0],j*Stride[1]:j*Stride[1]+Kernel.shape[1]]*Kernel).sum()
    return Y
# 测试案例
#corr2d_pad(torch.tensor([[1,2,3],[4,5,6],[5,6,7]]),torch.tensor([[1,2],[2,3]]),(1,1),(1,1))
#三维卷积无padding
def corr3d(Data,Kernel,Stride):
    Y=torch.zeros(((Data.shape[0]-Kernel.shape[0])//(Stride[0])+1,(Data.shape[1]-Kernel.shape[1])//(Stride[1])+1,(Data.shape[2]-Kernel.shape[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            for k in range(Y.shape[2]):
                Y[i,j,k]=(Data[i*Stride[0]:i*Stride[0]+Kernel.shape[0],j*Stride[1]:j*Stride[1]+Kernel.shape[1],k*Stride[2]:k*Stride[2]+Kernel.shape[2]]*Kernel).sum()
    return Y
# 测试案例
#corr3d(Data=torch.tensor([[[1,2,3],[4,5,6]],[[7,8,9],[1,2,3]]]),Kernel=torch.tensor([[[1,2],[1,1]],[[1,-1],[-1,2]]]),Stride=(1,1,1))
#三维卷积有padding
def corr3d_pad(Data,Kernel,Padding,Stride):
    Data=torch.concatenate((torch.zeros((Padding[0],Data.shape[1],Data.shape[2])),Data,torch.zeros((Padding[0],Data.shape[1],Data.shape[2]))),axis=0)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Padding[1],Data.shape[2])),Data,torch.zeros((Data.shape[0],Padding[1],Data.shape[2]))),axis=1)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Data.shape[1],Padding[2])),Data,torch.zeros((Data.shape[0],Data.shape[1],Padding[2]))),axis=2)
    Y=torch.zeros(((Data.shape[0]-Kernel.shape[0])//(Stride[0])+1,(Data.shape[1]-Kernel.shape[1])//(Stride[1])+1,(Data.shape[2]-Kernel.shape[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            for k in range(Y.shape[2]):
                Y[i,j,k]=(Data[i*Stride[0]:i*Stride[0]+Kernel.shape[0],j*Stride[1]:j*Stride[1]+Kernel.shape[1],k*Stride[2]:k*Stride[2]+Kernel.shape[2]]*Kernel).sum()
    return Y
# 测试案例
#corr3d_pad(Data=torch.tensor([[[1,2,3],[4,5,6]],[[7,8,9],[1,2,3]]]),Kernel=torch.tensor([[[1,2],[1,1]],[[1,-1],[-1,2]]]),Padding=(0,0,0),Stride=(1,1,1))
####################################################
#池化
#二维池化无padding
#def pool2d(Data,Mode='max,'avg'):
def pool2d(Data,Kernel,mode,Stride):
    Y=torch.zeros(((Data.shape[0]-Kernel[0])//(Stride[0])+1,(Data.shape[1]-Kernel[1])//(Stride[1])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode=='max':
                Y[i,j]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1]].max()
            elif mode=='mean':
                Y[i,j]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1]].mean()
    return Y
# 测试案例
#pool2d(torch.tensor([[1.,2,3],[4,5,6],[5,6,7.]]),(2,3),'mean',Stride=(1,1))
#二维池化有padding
def pool2d_pad(Data,Kernel,mode,Padding,Stride):
    Data=torch.concatenate((torch.zeros((Padding[0],Data.shape[1])),Data,torch.zeros((Padding[0],Data.shape[1]))),axis=0)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Padding[1])),Data,torch.zeros((Data.shape[0],Padding[1]))),axis=1)
    Y=torch.zeros(((Data.shape[0]-Kernel[0])//(Stride[0])+1,(Data.shape[1]-Kernel[1])//(Stride[1])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode=='max':
                Y[i,j]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1]].max()
            elif mode=='mean':
                Y[i,j]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1]].mean()
    return Y
# 测试案例
#pool2d_pad(torch.tensor([[1.,2,3],[4,5,6],[5,6,7]]),(2,2),'mean',(1,1),(1,1))
#三维池化无padding
def pool3d(Data,Kernel,mode,Stride):
    Y=torch.zeros(((Data.shape[0]-Kernel[0])//(Stride[0])+1,(Data.shape[1]-Kernel[1])//(Stride[1])+1,(Data.shape[2]-Kernel[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            for k in range(Y.shape[2]):
                if mode=='max':
                    Y[i,j,k]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1],k*Stride[2]:k*Stride[2]+Kernel[2]].max()
                elif mode=='mean':
                    Y[i,j,k]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1],k*Stride[2]:k*Stride[2]+Kernel[2]].mean()
    return Y
# 测试案例
#pool3d(Data=torch.tensor([[[1,2,3],[4,5,6]],[[7,8,9],[1,2,3]]]),Kernel=(2,2,2),mode='max',Stride=(1,1,1))
#三维池化有padding
def pool3d_pad(Data,Kernel,mode,Padding,Stride):
    Data=torch.concatenate((torch.zeros((Padding[0],Data.shape[1],Data.shape[2])),Data,torch.zeros((Padding[0],Data.shape[1],Data.shape[2]))),axis=0)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Padding[1],Data.shape[2])),Data,torch.zeros((Data.shape[0],Padding[1],Data.shape[2]))),axis=1)
    Data=torch.concatenate((torch.zeros((Data.shape[0],Data.shape[1],Padding[2])),Data,torch.zeros((Data.shape[0],Data.shape[1],Padding[2]))),axis=2)
    Y=torch.zeros(((Data.shape[0]-Kernel[0])//(Stride[0])+1,(Data.shape[1]-Kernel[1])//(Stride[1])+1,(Data.shape[2]-Kernel[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            for k in range(Y.shape[2]):
                if mode=='max':
                    Y[i,j,k]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1],k*Stride[2]:k*Stride[2]+Kernel[2]].max()
                elif mode=='mean':
                    Y[i,j,k]=Data[i*Stride[0]:i*Stride[0]+Kernel[0],j*Stride[1]:j*Stride[1]+Kernel[1],k*Stride[2]:k*Stride[2]+Kernel[2]].mean()
    return Y
# 测试案例
#pool3d_pad(Data=torch.tensor([[[1,2,3],[4,5,6]],[[7,8,9],[1,2,3]]]),Kernel=(2,2,2),mode='max',Padding=(0,0,0),Stride=(1,1,1))
#二维测试
#Data=torch.randn(5,5)
#Kernel=torch.randn(3,3)
#Stride=(1,1)
#Padding=(1,1)
#print(Data,Kernel,Stride)
#print((Data[1:4,1:4]*Kernel).sum())
#Y=corr2d_pad(Data,Kernel,Stride,Padding)
#print(Y)
#Z=pool2d_pad(Y,Kernel=(3,3),mode='max',Padding=(1,1),Stride=(1,1))
#print(Z)
#三维测试
#Data=torch.randn(5,5,5)
#Kernel=torch.randn(3,3,3)
#Stride=(1,1,1)
#Padding=(1,1,1)
#print(Data,Kernel,Padding,Stride)
#print((Data[1:4,1:4,2:5]*Kernel).sum())
#Y=corr3d_pad(Data=Data,Kernel=Kernel,Padding=Padding,Stride=Stride)
#print(Y)
#Z=pool3d_pad(Y,Kernel=(3,3,3),mode='max',Padding=(1,1,1),Stride=(1,1,1))
#print(Z)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125

然后定义卷积层和池化层

#定义卷积层操作无padding
#下面是二维样本特征时多样本多输出的卷积层
def convnet_2d(Data,Kernel,bias,Padding,Stride):
    Y=torch.zeros((Data.shape[0],Kernel.shape[0],(Data.shape[1]-Kernel.shape[1]+2*Padding[0])//(Stride[0])+1,(Data.shape[2]-Kernel.shape[2]+2*Padding[1])//(Stride[1])+1))
    #第几个样本
    for i in range(Y.shape[0]):
        #第几个输出内核
        for j in range(Y.shape[1]):
            Y[i,j,:,:]=corr2d_pad(Data[i,:,:].reshape(Data.shape[1:]),Kernel[j,:,:].reshape(Kernel.shape[1:]),Padding,Stride)
            Y[i,j,:,:]+=bias[j]        
    Y=1/(1+torch.exp(-Y))
    return Y
#测试
#Kernel=torch.randn((4,3,3),requires_grad=True)
#bias=torch.randn((Kernel.shape[0],1),requires_grad=True)
#convnet_2d(torch.randn(1,7,7),Kernel,bias,Padding=(1,1),Stride=(1,1))
#定义完整的二维样本卷积层
#def conv_2d(Data=(样本数,输入通道数,特征),Kernel=(输出通道数,输入通道数,二维卷积核),bias=(输出通道数,1),Padding=(二维扩充尺寸),Stride=(二维步进尺寸))->(样本数,输出通道数,卷积结果)
def convnet2d(Data,Kernel,bias,Padding,Stride):
    Y=torch.zeros((Data.shape[0],Kernel.shape[0],(Data.shape[2]-Kernel.shape[2]+2*Padding[0])//Stride[0]+1,(Data.shape[3]-Kernel.shape[3]+2*Padding[1])//Stride[1]+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j,:,:]=corr3d_pad(Data[i,:,:,:].reshape(Data.shape[1:]),Kernel[j,:,:,:].reshape(Kernel.shape[1:]),(0,Padding[0],Padding[1]),(1,Stride[0],Stride[1])).reshape(Y.shape[2],Y.shape[3])
            Y[i,j,:,:]+=bias[j]
    Y=1/(1+torch.exp(-Y))
    return Y
#每个(输出通道,输入通道)组合都有一个偏置还是每个输出通道才有偏置，还是每个输入通道有偏置？还是每个卷积核都有一个偏置？
#前面的输出矩阵的尺寸容易理解，找几个例子推算一下就清楚了，
#下面是三维样本特征时多样本多输出的卷积层
def convnet_3d(Data,Kernel,bias,Padding,Stride):
    Y=torch.zeros((Data.shape[0],Kernel.shape[0],(Data.shape[1]-Kernel.shape[1]+2*Padding[0])//(Stride[0])+1,(Data.shape[2]-Kernel.shape[2]+2*Padding[1])//(Stride[1])+1,(Data.shape[3]-Kernel.shape[3]+2*Padding[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j,:,:,:]=corr3d_pad(Data[i,:,:,:].reshape(Data.shape[1:]),Kernel[j,:,:,:].reshape(Kernel.shape[1:]),Padding,Stride)
            Y[i,j,:,:,:]+=bias[j]
    Y=1/(1+torch.exp(-Y))
    return Y
#测试
#Kernel=torch.randn((4,3,3,3),requires_grad=True)
#bias=torch.randn((Kernel.shape[0],1),requires_grad=True)
#convnet_3d(torch.randn(1,7,7,7),Kernel,bias,Padding=(1,1,1),Stride=(1,1,1))
#下面是二维样本特征多样本多输出的汇聚层。
def poolnet_2d(Data,Kernel,mode,Padding,Stride):
    Y=torch.zeros((Data.shape[0],Data.shape[1],(Data.shape[2]-Kernel[0]+2*Padding[0])//(Stride[0])+1,(Data.shape[3]-Kernel[1]+2*Padding[1])//(Stride[1])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j,:,:]=pool2d_pad(Data[i,j,:,:].reshape(Data.shape[2:]),Kernel,mode,Padding,Stride)
    return Y
#测试
#Kernel=torch.randn((4,3,3),requires_grad=True)
#bias=torch.randn((Kernel.shape[0],1),requires_grad=True)
#Y=convnet_2d(torch.randn(1,7,7),Kernel,bias,Padding=(1,1),Stride=(1,1))
#print(Y)
#Z=poolnet_2d(Y,Kernel=(3,3),mode='max',Padding=(1,1),Stride=(1,1))
#print(Z)
#下面是三维样本特征多样本多输出的汇聚层
def poolnet_3d(Data,Kernel,mode,Padding,Stride):
    Y=torch.zeros((Data.shape[0],Data.shape[1],(Data.shape[2]-Kernel[0]+2*Padding[0])//(Stride[0])+1,(Data.shape[3]-Kernel[1]+2*Padding[1])//(Stride[1])+1,(Data.shape[4]-Kernel[2]+2*Padding[2])//(Stride[2])+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j,:,:,:]=pool3d_pad(Data[i,j,:,:,:].reshape(Data.shape[2:]),Kernel,mode,Padding,Stride)
    return Y
#测试
#Kernel=torch.randn((4,3,3,3),requires_grad=True)
#bias=torch.randn((Kernel.shape[0],1),requires_grad=True)
#Y=convnet_3d(torch.randn(1,7,7,7),Kernel,bias,Padding=(1,1,1),Stride=(1,1,1))
#print(Y)
#Z=poolnet_3d(Y,Kernel=(3,3,3),mode='max',Padding=(1,1,1),Stride=(1,1,1))
#print(Z)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

对于二维结构的数据我写了一个代码，数据是二维$(28,28)$的，标签是$(1,10)$，相当于它属于10个类别中各个类别的概率。然后我们通过卷积神经网络Lenet来学习出模型对于样本数据归属于各个类别的预测概率$(1,10)$，然后我们用真实概率与预测概率之间的交叉熵来作为损失函数，对损失函数求极小就相当与极大似然估计。

torch.set_default_tensor_type(torch.cuda.FloatTensor)
torch.manual_seed(1)
Data1=torch.randn((10,1,28,28))
label=torch.randn((10,10))
Label1=torch.exp(label)/torch.exp(label).sum(axis=1).reshape(10,1)
lr=0.03
Kernel1=torch.randn((6,1,5,5),requires_grad=True)
bias1=torch.randn((Kernel1.shape[0],1),requires_grad=True)
Padding1=(2,2)
Stride1=(1,1)
Kernel2=torch.randn((16,6,5,5),requires_grad=True)
bias2=torch.randn((Kernel2.shape[0],1),requires_grad=True)
weight1=torch.randn((400,120),requires_grad=True)
weight2=torch.randn((120,84),requires_grad=True)
weight3=torch.randn((84,10),requires_grad=True)
for tt in range(1000):
    C1=convnet2d(Data=Data1,Kernel=Kernel1,bias=bias1,Padding=Padding1,Stride=Stride1)
    print(C1.shape)
    P1=poolnet_2d(C1,Kernel=(2,2),mode='mean',Padding=(0,0),Stride=(2,2))
    print(P1.shape)
    C2=convnet2d(P1,Kernel2,bias2,Padding=(0,0),Stride=(1,1))
    print(C2.shape)
    P2=poolnet_2d(C2,Kernel=(2,2),mode='mean',Padding=(0,0),Stride=(2,2))
    print(P2.shape)
    Y=torch.zeros((P2.shape[0],P2.shape[1]*P2.shape[2]*P2.shape[3]))
    for i in range(P2.shape[0]):
        Y[i,:]=P2[i,:,:,:].reshape(1,-1)
    Y1=1/(1+torch.exp(-torch.mm(Y,weight1)))
    Y2=1/(1+torch.exp(-torch.mm(Y1,weight2)))
    Y3=torch.exp(torch.mm(Y2,weight3))/(torch.exp(torch.mm(Y2,weight3))).sum(axis=1).reshape(Y2.shape[0],1)
    print(Y3[0,:])
    #上面输出的是全链接层的结果
    #我们思考一下损失函数怎么定义，从结果上来看是概率分布的交叉熵，从实际上来看应该是最大似然函数。
    loss=(-1*Label1*torch.log(Y3)).sum()
    loss.backward()
    Kernel1.data=Kernel1.data-lr*Kernel1.grad.data
    bias1.data=bias1.data-lr*bias1.grad.data
    Kernel2.data=Kernel2.data-lr*Kernel2.grad.data
    bias2.data=bias2.data-lr*bias2.grad.data
    weight1.data=weight1.data-lr*weight1.grad.data
    weight2.data=weight2.data-lr*weight2.grad.data
    weight3.data=weight3.data-lr*weight3.grad.data
    Kernel1.grad.data.zero_()
    bias1.grad.data.zero_()
    Kernel2.grad.data.zero_()
    bias2.grad.data.zero_()
    weight1.grad.data.zero_()
    weight2.grad.data.zero_()
    weight3.grad.data.zero_()
    print(loss,Y3[0,:],Label1[0,:])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

原本是用100个样本数据，但是计算过程中发现loss会越来越大，所以我们用十个样本检测一下。发现代码没有什么问题，损失函数的确是照常减小的，不过由于我设置的迭代系数太大了，所以最后发生了震荡现象。

torch.Size([10, 6, 28, 28])
torch.Size([10, 6, 14, 14])
torch.Size([10, 16, 10, 10])
torch.Size([10, 16, 5, 5])
tensor([0.0726, 0.0859, 0.0348, 0.0326, 0.3475, 0.0653, 0.0459, 0.0686, 0.1554,
        0.0915], grad_fn=<SliceBackward0>)
tensor(20.8011, grad_fn=<SumBackward0>) tensor([0.0726, 0.0859, 0.0348, 0.0326, 0.3475, 0.0653, 0.0459, 0.0686, 0.1554,
        0.0915], grad_fn=<SliceBackward0>) tensor([0.0835, 0.0828, 0.0829, 0.0370, 0.2457, 0.0858, 0.0649, 0.0610, 0.1569,
        0.0995])
torch.Size([10, 6, 28, 28])
torch.Size([10, 6, 14, 14])
torch.Size([10, 16, 10, 10])
torch.Size([10, 16, 5, 5])
tensor([0.1160, 0.0891, 0.1459, 0.0681, 0.1331, 0.0948, 0.0592, 0.0534, 0.1372,
        0.1030], grad_fn=<SliceBackward0>)
tensor(20.7234, grad_fn=<SumBackward0>) tensor([0.1160, 0.0891, 0.1459, 0.0681, 0.1331, 0.0948, 0.0592, 0.0534, 0.1372,
        0.1030], grad_fn=<SliceBackward0>) tensor([0.0835, 0.0828, 0.0829, 0.0370, 0.2457, 0.0858, 0.0649, 0.0610, 0.1569,
        0.0995])
torch.Size([10, 6, 28, 28])
torch.Size([10, 6, 14, 14])
torch.Size([10, 16, 10, 10])
torch.Size([10, 16, 5, 5])
tensor([0.0594, 0.0913, 0.0349, 0.0324, 0.3525, 0.0647, 0.0453, 0.0690, 0.1626,
        0.0879], grad_fn=<SliceBackward0>)
tensor(20.8868, grad_fn=<SumBackward0>) tensor([0.0594, 0.0913, 0.0349, 0.0324, 0.3525, 0.0647, 0.0453, 0.0690, 0.1626,
        0.0879], grad_fn=<SliceBackward0>) tensor([0.0835, 0.0828, 0.0829, 0.0370, 0.2457, 0.0858, 0.0649, 0.0610, 0.1569,
        0.0995])
torch.Size([10, 6, 28, 28])
torch.Size([10, 6, 14, 14])
torch.Size([10, 16, 10, 10])
torch.Size([10, 16, 5, 5])
tensor([0.1361, 0.0833, 0.1455, 0.0688, 0.1243, 0.0958, 0.0596, 0.0526, 0.1243,
        0.1098], grad_fn=<SliceBackward0>)
tensor(20.8619, grad_fn=<SumBackward0>) tensor([0.1361, 0.0833, 0.1455, 0.0688, 0.1243, 0.0958, 0.0596, 0.0526, 0.1243,
        0.1098], grad_fn=<SliceBackward0>) tensor([0.0835, 0.0828, 0.0829, 0.0370, 0.2457, 0.0858, 0.0649, 0.0610, 0.1569,
        0.0995])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

我们以第一个样本数据的标签为例：$tensor([0.0835,0.0828,0.0829,0.0370,0.2457,0.0858,0.0649,0.0610,0.1569,0.0995])$。
模型训练出来的估计概率是：
$tensor([0.0594,0.0913,0.0349,0.0324,0.3525,0.0647,0.0453,0.0690,0.1626,0.0879],gra{d}_{f}n=<SliceBackward0>)$，
$tensor([0.1361,0.0833,0.1455,0.0688,0.1243,0.0958,0.0596,0.0526,0.1243,0.1098],gra{d}_{f}n=<SliceBackward0>)$
也就是上面倒数两个估计结果，时大时小，发生了震荡。说明我的0.03太大了，应该调小一些。