【C++刷题】二叉树进阶刷题

1. 根据二叉树创建字符串

class Solution {
public:
	/*
	* ()的省略有两种情况
	* 1.左右都为空，省略
	* 2.左子树不为空，右子树为空，省略
	*/
    string tree2str(TreeNode* root)
    {
        string s;
        if(root == nullptr)
        {
            return s;
        }
       
        s += to_string(root->val);
        if(root->left)
        {
            s += "(";
            s += tree2str(root->left);
            s +=")";
        }
        else if(root->right) // 为了应对左为空，右不为空的情况
        {
            s += "()";
        }
        
        if(root->right)
        {
            s += "(";
            s += tree2str(root->right);
            s += ")";
        }
        
        return s;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

2. 二叉树的层序遍历

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root)
    {
        vector<vector<int>> vv;
        queue<TreeNode*> q;
        int levelSize = 0;

        if(root == nullptr)
        {
            return vv;
        }

        q.push(root);
        vector<int> v;
        while(!q.empty())
        {
            v.resize(0);
            levelSize = q.size();
            while(levelSize--)
            {
                if((q.front())->left)
                {
                    q.push((q.front())->left);
                }
                if((q.front())->right)
                {
                    q.push((q.front())->right);
                }
                v.push_back((q.front())->val);
                q.pop();
            }
            vv.push_back(v);
        }

        return vv;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

3. 二叉树的层序遍历 II

只需将正着层序遍历的结果reverse()一下即可。

4. 二叉树的最近公共祖先

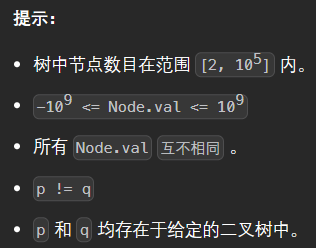
class Solution {
public:
    bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& st)
    {
        if(root == nullptr)
        {
            return false;
        }

        st.push(root);
        if(root == x)
        {
            return true;
        }

        if(FindPath(root->left, x, st))
        {
            return true;
        }
        if(FindPath(root->right, x, st))
        {
            return true;
        }
        st.pop();
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
    {
            stack<TreeNode*> pPath, qPath;
            FindPath(root, p, pPath); // 找从根节点root到p的路径
            FindPath(root, q, qPath); // 找从根节点root到q的路径

            while(pPath.size() != qPath.size())
            {
                if(pPath.size() > qPath.size())
                {
                    pPath.pop();
                } 
                else
                {
                    qPath.pop();
                }
            }

            while(pPath.top() != qPath.top())
            {
                pPath.pop();
                qPath.pop();
            }

            return pPath.top();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

5. 二叉搜索树与双向链表

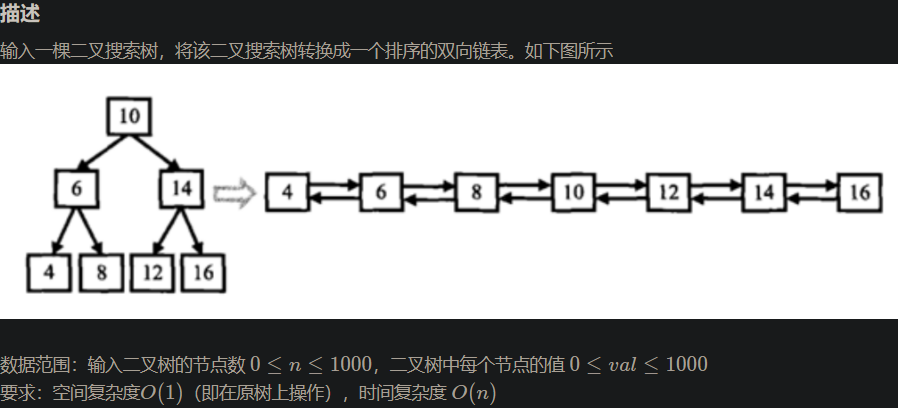
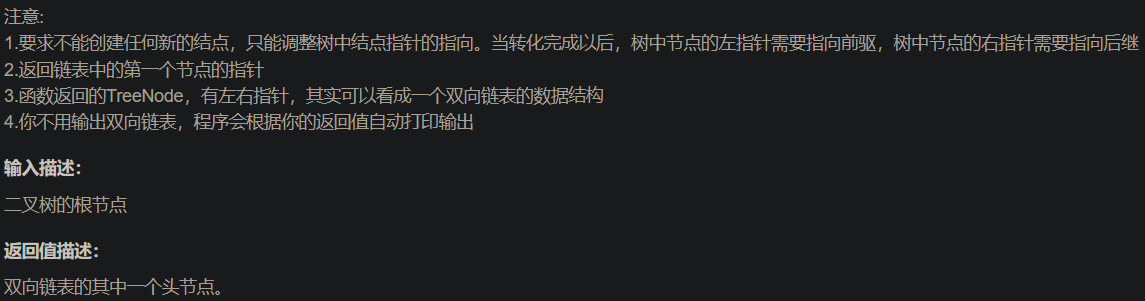
class Solution {
public:
	void InOrderConvert(TreeNode* cur, TreeNode*& prev)
	{
		if(cur == nullptr)
		{
			return;
		}

		InOrderConvert(cur->left, prev);
		// 双向链接
		cur->left = prev;
		if(prev)
		{
			prev->right = cur;
		}
		// prev向后移
		prev = cur;
		InOrderConvert(cur->right, prev);
	}
    TreeNode* Convert(TreeNode* pRootOfTree)
	{
		TreeNode* prev = nullptr;
		// 中序遍历进行链接
		InOrderConvert(pRootOfTree, prev);
		
		// 找头节点
		TreeNode* head = pRootOfTree;
		while(head && head->left)
		{
			head = head->left;
		}

		return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

6. 从前序与中序遍历序列构造二叉树

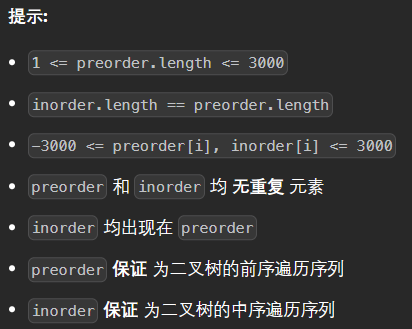
class Solution {
public:
	// 法一
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
    {
    	// 子树区间确认是否继续递归创建子树
        if(inbegin > inend)
            return nullptr;
            
        // 前序创建树
        TreeNode* root = new TreeNode(preorder[prei++]);
        // 中序分割左右子树
        int ini = inbegin;
        while(ini <= inend)
        {
            if(inorder[ini] == root->val)
                break;
            else
                ++ini;
        }
        
        root->left = _buildTree(preorder, inorder, prei, inbegin, ini - 1);
        root->right = _buildTree(preorder, inorder, prei, ini + 1, inend);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
        int i = 0;
        return _buildTree(preorder, inorder, i, 0, inorder.size() - 1);
    }

	// 法二
	TreeNode* buildTreeHelper(vector<int>& preorder, size_t preStart, size_t preEnd, vector<int>& inorder, size_t inStart, size_t inEnd)
    {
        if(preStart >= preEnd)
        {
            return nullptr;
        }
        TreeNode* root = new TreeNode(preorder[preStart]);
        // [preStart + 1, preStart + 1 + i - vinStart) [preStart + 1 + i - vinStart, preEnd)
        // [vinStart, i) i [i + 1, vinEnd)
        for(size_t i = inStart; i < inEnd; ++i)
        {
            if(inorder[i] == root->val)
            {
                root->left = buildTreeHelper(preorder, preStart + 1, preStart + 1 + i - inStart, inorder, inStart, i);
                root->right = buildTreeHelper(preorder, preStart + 1 + i - inStart, preEnd, inorder, i + 1, inEnd);
                break;
            }
        }

        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
        return buildTreeHelper(preorder, 0, preorder.size(), inorder, 0, inorder.size());
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

7. 从中序与后序遍历序列构造二叉树

// 法一
class Solution {
public:
    TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posti, int inbegin, int inend)
    {
        if(inbegin > inend)
            return nullptr;

        TreeNode* root = new TreeNode(postorder[posti--]);

        int ini = inbegin;
        while(ini <= inend)
        {
            if(inorder[ini] == root->val)
                break;
            else
                ++ini;
        }

        root->right = _buildTree(inorder, postorder, posti, ini + 1, inend);
        root->left = _buildTree(inorder, postorder, posti, inbegin, ini - 1);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
    {
        int i = postorder.size() - 1;
        return _buildTree(inorder, postorder, i, 0, inorder.size() - 1);
    }
};

// 法二
TreeNode* buildTreeHelper(vector<int>& inorder, size_t inStart, size_t inEnd, vector<int>& postorder, size_t postStart, size_t postEnd)
    {
        if(inStart >= inEnd)
        {
            return nullptr;
        }
        TreeNode* root = new TreeNode(postorder[postEnd - 1]);
        // [postStart, postEnd - 1 - (inEnd - i - 1)) [postEnd - 1 - (inEnd - i - 1), postEnd - 1)
        // [inStart, i) i [i + 1, inEnd)
        for(size_t i = inStart; i < inEnd; ++i)
        {
            if(inorder[i] == root->val)
            {
                root->left = buildTreeHelper(inorder, inStart, i, postorder, postStart, postEnd - 1 - (inEnd - i - 1));
                root->right = buildTreeHelper(inorder, i + 1, inEnd, postorder, postEnd - 1 - (inEnd - i - 1), postEnd - 1);
                break;
            }
        }

        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
    {
        return buildTreeHelper(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57