《动手学深度学习 Pytorch版》 4.2 多层感知机的从零开始实现

import torch
from torch import nn
from d2l import torch as d2l

# 经典数据集与batch size
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
1
2
3
4
5
6
7

4.2.1 初始化模型

为什么不直接使用 Tensor 而是用 nn.Parameter 函数将其转换为 parameter呢？

nn.Parameter 函数会向宿主模型注册参数，从而在参数优化的时候可以自动一起优化。

此外，由于内存在硬件中的分配和寻址方式，选择2的若干次幂作为层宽度会使计算更高效。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

# 输入层参数
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
# 隐藏层参数
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]
1
2
3
4
5
6
7
8
9
10
11
12

4.2.2 激活函数

def relu(X):  # 自定义 ReLU 函数
    a = torch.zeros_like(X)
    return torch.max(X, a)
1
2
3

4.2.3 模型

由于忽略了空间结构，我们调用 reshape 函数将每个二维图像转换成长度为 num_inputs 的向量。

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 输入层运算+激活 这里“@”代表矩阵乘法
    return (H@W2 + b2)  # 隐藏层运算
1
2
3
4

4.2.4 损失函数

loss = nn.CrossEntropyLoss(reduction='none')  # 使用交叉熵损失函数
1

4.2.5 训练

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)  # 优化算法
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
1
2
3

​

​

d2l.predict_ch3(net, test_iter)  # 在一些测试集上运行一下这个模型
1

​

​

练习

（1）在所有其他参数保持不变的情况下，更改超参数 num_hiddens 的值，并查看此超参数值的变化对结果有何影响。确定此超参数的最佳值。

num_epochs, lr = 10, 0.1

for num_hiddens in [32, 64, 128, 256, 512, 1024, 2048]:
    num_inputs, num_outputs = 784, 10
    # 输入层参数
    W1 = nn.Parameter(torch.randn(
        num_inputs, num_hiddens, requires_grad=True) * 0.01)
    b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
    # 隐藏层参数
    W2 = nn.Parameter(torch.randn(
        num_hiddens, num_outputs, requires_grad=True) * 0.01)
    b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
    params = [W1, b1, W2, b2]

    updater = torch.optim.SGD(params, lr=lr)
    d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

​

​

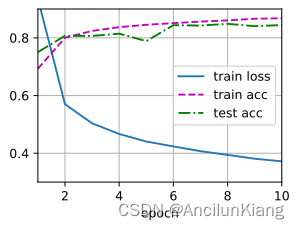
num_hiddens 越大训练效果越好

---

（2）尝试添加更多的隐藏层，并查看对结果有何影响。

def net2(X):
    X = X.reshape((-1, num_inputs))
    H1 = relu(X@W1 + b1)  # 输入层运算+激活 这里“@”代表矩阵乘法
    H2 = relu(H1@W2 + b2)
    return (H2@W3 + b3)  # 隐藏层运算

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 64
# 输入层参数
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens1, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens1, requires_grad=True))
# 隐藏层1参数
W2 = nn.Parameter(torch.randn(
    num_hiddens1, num_hiddens2, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_hiddens2, requires_grad=True))
# 隐藏层2参数
W3 = nn.Parameter(torch.randn(
    num_hiddens2, num_outputs, requires_grad=True) * 0.01)
b3 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2, W3, b3]

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net2, train_iter, test_iter, loss, num_epochs, updater)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

​

​

咋加了一层效果还差了一点点

---

（3）改变学习率会如何影响结果？保持模型架构和其他超参数（包括轮数）不变，学习率设置为多少会带来最佳结果？

num_epochs = 10

for lr in [0.05, 0.1, 0.2, 0.3, 0.4, 0.5]:
    num_inputs, num_outputs, num_hiddens = 784, 10, 256
    # 输入层参数
    W1 = nn.Parameter(torch.randn(
        num_inputs, num_hiddens, requires_grad=True) * 0.01)
    b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
    # 隐藏层参数
    W2 = nn.Parameter(torch.randn(
        num_hiddens, num_outputs, requires_grad=True) * 0.01)
    b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
    params = [W1, b1, W2, b2]

    updater = torch.optim.SGD(params, lr=lr)
    d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

​

​

---

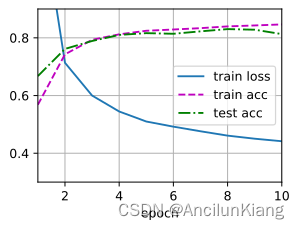
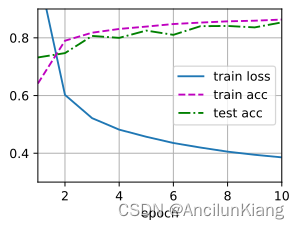
（4）通过对所有超参数（学习率、轮数、隐藏层数、每层的隐藏单元数）进行联合优化，可以得到的最佳结果是什么？

def net2(X):
    X = X.reshape((-1, num_inputs))
    H1 = relu(X@W1 + b1)  # 输入层运算+激活 这里“@”代表矩阵乘法
    H2 = relu(H1@W2 + b2)
    return (H2@W3 + b3)  # 隐藏层运算

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 128
# 输入层参数
W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens1, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens1, requires_grad=True))
# 隐藏层1参数
W2 = nn.Parameter(torch.randn(
    num_hiddens1, num_hiddens2, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_hiddens2, requires_grad=True))
# 隐藏层2参数
W3 = nn.Parameter(torch.randn(
    num_hiddens2, num_outputs, requires_grad=True) * 0.01)
b3 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2, W3, b3]

num_epochs, lr = 10, 0.3
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net2, train_iter, test_iter, loss, num_epochs, updater)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

​

​

---

（5）描述为什么涉及多个超参数更具挑战性。

高情商：更具挑战性

低情商：玄学

---

（6）如果想要构建多个超参数搜索方法，请设计一个聪明的策略。

笨笨的我想不出聪明的策略，智能上网搜了。

1. 网格搜索（Grid Search）：相当于利用穷举法自动调参。

2. 随机搜索（Random Search）：相交网格搜索会更快，但是也可能掠过最优解。