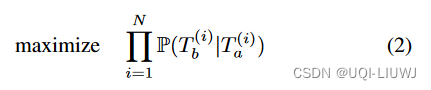论文笔记：Deep Representation Learning for Trajectory Similarity Computation

ICDE 2018

1 intro

1.1 背景

• 用于计算轨迹相似性的成对点匹配方法（DTW，LCSS，EDR，ERP）的问题：
  • 轨迹的采样率不均匀
    • 如果两个轨迹表示相同的基本路径，但是以不同的采样率生成，那么这些方法很难将它们识别为相似的轨迹
    • 
  • 当样本点的采样率很低时，很难对齐相似轨迹的样本点
  • 当样本点噪声时，这些方法的性能可能会下降。
  • 复杂度大O(n^2)【n是轨迹长度】

1.2 论文贡献

• 论文提出t2vec，基于深度表示学习推断和表示轨迹的基本路径信息
  • 通过利用存档的历史轨迹数据和一个新的深度学习框架来实现的
  • 计算两个轨迹之间的相似性只需要线性时间O(n + |v|) (|v|是向量v的长度)
• 为了学习轨迹表示，自然地考虑使用RNN。但是简单地应用RNNs来嵌入轨迹是不切实际的
  • 使用RNNs获得的表示不能在由于低采样率或噪声引起的不确定性下揭示轨迹的最可能的真实路径
    • ——>提出了一个seq2seq模型，以最大化恢复轨迹真实路径的概率
  • 用于训练RNNs的现有损失函数没有考虑空间接近性
    • ——>设计了一个空间接近性感知的损失函数和一个单元预训练算法，鼓励模型为由相同路径生成的轨迹学习一致的表示’
• 还提出了使用噪声对比估计的近似损失函数，以提高训练速度

2 问题定义和preliminary

2.1 定义

• 基本路径
  • 基本路径是一个连续的空间曲线，表示对象所走的确切路径
  • 本路径只是一个理论概念，因为位置获取技术不连续地记录移动位置
• 轨迹
  • 轨迹T是从移动对象的基本路径中得到的样本点的序列

2.2 问题定义

• 给定一组历史轨迹，我们的目标是为每个轨迹T学习一个表示v∈Rn，使得该表示可以反映轨迹的基本路径，用于计算轨迹相似性

2.3 sequence encoder-decoder

• 两个序列，其中每个xt​ 和 yt​ 表示一个token

• 编码器用于将序列x编码为一个固定维度的向量v，该向量保留了x中的顺序信息，然后解码器根据编码的表示v解码出序列y
• RNN接受实值向量形式的输入，因此添加了一个token嵌入层来将离散token嵌入到一个向量中

• 计算P(y|x)【链式法则】
  • 
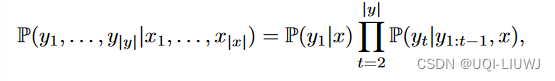
    • 由于v编码了x中的顺序信息，我们有:
      • 
    •  
      • 
      • EOS是一个特殊的token，表示序列的结束

3 方法

• 基本路径R在实践中通常是不可用的，为了绕过这个问题，论文利用两个观察
  • 非均匀、相对低采样率轨迹，表示为Ta；相对高采样率轨迹，表示为Tb
  • 相对高采样率的轨迹Tb比Ta更接近它们的真实基本路径R，它的不确定性更低
• ——>最大化P(R∣Ta) 的目标替换为最大化P(Tb∣Ta)
• 编码器将Ta嵌入到其表示v中，然后解码器将尝试恢复其相对高采样率的配对Tb

3.1 处理变化的采样率和噪声

• 给定一组轨迹集合
  • N是集合的元素数量
  • 创建一组对 (Ta, Tb)，其中Tb是一个原始轨迹，Ta是通过从Tb中随机丢弃样本点（丢弃率为r1）获得的
  • ——>每一个下采样的Ta也是非均匀采样的，因此代表一个具有非均匀和低采样率的实际轨迹
  • Tb的起点和终点在Ta中得到保留，以避免改变下采样轨迹的基本路径
• 生成过程之后，我们使用序列编码器-解码器模型最大化所有(Ta, Tb)对的联合概率：
  • 
• 在序列编码器-解码器模型中，输入应该是离散token的序列
  • 将空间分割成等大小的单元，并将每个单元视为一个token
  • 所有落入同一单元的样本点都被映射到同一token
    • ——>有助于克服非均匀和低采样率的问题
• 现实的轨迹也可能有噪声样本点
  • 为了消除噪声样本点的影响，只保留被超过δ个样本点击中的单元
  • 这些单元被称为热单元，并形成最终的词汇V
  • 样本点由它们最近的热单元表示
• 为了使学习到的表示对噪声数据更加鲁棒，我们进一步扭曲每一个下采样的Ta，基于一个扭曲率r2来创建扭曲的变体
  • 随机采样一部分点（由r2指示的大小），然后扭曲它们

3.2 学习表征

• 原始的序列编码器-解码器并没有对单元间的空间关联进行建模
• ——>论文提出了一个新的空间接近性感知损失函数和一个新的考虑空间接近性的单元表示预训练方法。
• ——>为了进一步提高训练效果，还提出了基于噪声对比估计的近似损失函数

3.2.1 空间接近性感知损失函数

• 损失函数的差异会鼓励模型学习不同的表示[32]
• NLP中的损失函数大多为NLL
  • 
    • 简单地采用这个损失函数对于时空数据是有问题的
    • 
      • 图3中有两个从同一路线 R 生成的轨迹 Tb 和 Tb′ （在坐标转换为单元后，它们的对应序列分别是 y 和 ′y′ ）
      • 轨迹的样本点交错在我们的空间分区中的单元
      • 设 Ta 和 Ta′ 分别表示 Tb 和 Tb′ 的子轨迹
        • 理想情况下，为 Ta 和 Ta′ 学习到的表示应该是相似的，因为它们都是从路线 R 生成的
        • 方程4中的NLL损失函数将 Tb 和 T′b 区分为两个相同的目标轨迹，因此它不能发现 Ta 和 T′a 之间的相似性
        • ——>这是因为方程4中的损失函数对输出单元进行了等权重的惩罚
        • 直观地说，接近目标的输出单元应该比远离目标的输出单元更可接受
          • 如果解码的目标单元是y3，损失函数会对输出y′3和y1进行相同的惩罚。这不是一个好的惩罚策略。
          • 因为y′3在空间上离y3更近，所以对于解码器输出y′3而不是输出y1来说，这是更可接受的
• ——>空间接近性感知损失函数背后的直觉是，当我们试图从解码器解码目标单元yt时，我们为每个单元分配一个权重
  • 单元u ∈ V的权重与其与目标单元yt的空间距离成反比，因此单元离yt越近，我们将为其分配的权重越大
  • 
• 尽管方程5中的空间接近性感知损失函数帮助我们为从同一路线生成的轨迹学习一致的表示，但每次我们解码目标yt时，都需要对整个词汇进行两次求和：
  • 
  • 当词汇大小 ∣V∣ 很大时，训练模型的成本将会很高（时间复杂度O(|y|×|V|）

3.2.2 近似空间接近性感知损失函数

• 为了减少训练成本，根据以下两个观察设计了一个近似的空间接近性感知损失函数
  • 除了接近目标单元 yt 的单元外，大多数 wuyt​ 都非常小
    • 仅使用 yt 的K个最近的单元
    • 
  • 不需要计算方程6中的对数概率的确切值，只要我们可以鼓励解码器将概率分配给接近目标单元的单元
    • 使用噪声对比估计(NCE)来计算方程6中的对数概率
    • 类似于负采样
      • 从V−NK(yt) 随机抽样得到一小部分单元作为噪声数据来近似地最大化
      • 
  • ——>时间复杂度从O(∣y∣×∣V∣) 降低到O(∣y∣)

3.3 预训练单元表示

• 为了进一步确保由相同路线生成的轨迹在潜在空间中有接近的表示，论文提出了一个单元表示学习算法，用于预训练模型嵌入层中的单元
  • 为空间上接近的单元学习相似的表示
• 有两种直接的单元表示，都存在问题
  • one-hot
    • 失去了单元的空间距离关系，因为所有单元都被独立对待
    • 所提出的模型可能需要更多的训练时间来在单元嵌入层中发现空间关系
  • 单元的质心坐标（GPS坐标）
    • 自然地为单元编码了空间接近性
    • 但是将表示限制在一个二维空间中，这使得损失函数很难在它们的参数空间中进一步优化表示
• 借鉴skip-grams捕获单元空间接近性
  • skip-grams背后的直觉是，意义相似的词语往往在相同的上下文中出现，如果我们使用一个词的表示来预测其周围的词，那么我们可以以一种捕获词语之间的语义距离的方式将词嵌入到欧几里得空间中
  • 论文通过根据对单元随机采样其邻居u′ ∈ NK(u)（也只考虑其K个最近的邻居），为给定的单元u ∈ V创建上下文
    • 
• 此单元采样分布与方程5中的空间接近性权重类似
  • 他们的θ值不必相等
• 对于每个单元u∈V，单元采样分布倾向于采样与其空间接近的单元作为其上下文
  • 通过最大化观察到给定单元u的其上下文中的相邻单元的对数概率C(u)
  • 

3.4 复杂度

需要O(n)时间将轨迹嵌入到一个向量中

O(|v|)比较两个向量的欧几里得距离，来衡量两个轨迹的相似性

衡量两个轨迹之间的相似性的时间复杂性为O(n + |v|)

4 实验

4.1 数据集

• 波尔图轨迹
  • 19个月，包含170万轨迹
  • 每辆出租车每15秒报告一次其位置
  • 移除了长度小于30的轨迹，得到了120万轨迹
• 哈尔滨轨迹
  • 8个月内从13,000辆出租车中收集的轨迹
  • 选择长度至少为30的轨迹，并且连续采样点之间的时间间隔小于20秒。这产生了150万轨迹

4.2 衡量标准

• 相似轨迹搜寻
  • 从测试数据集中随机选择10,000个轨迹，记为Q
  • 选择另外m个轨迹，记为P
  • 对于每一个轨迹Tb ∈ Q，我们通过从中交替取点来创建它的两个子轨迹，分别记为Ta和Ta′，并使用它们构建两个数据集DQ = {Ta}和D′ Q = {Ta′ }
    • 
  • 对P中的轨迹执行相同的转换，得到DP和D′ P
  • 然后，对于每一个查询Ta ∈ DQ，我们从数据库D′ Q ∪ D′ P中检索其前k个最相似的轨迹，并计算Ta′的排名
• 理想情况下，Ta′应该排在最前面，因为它是由与Ta相同的原始轨迹生成的
• 使用D′ Q ∪ D′ P作为数据库而不是D′ Q ∪ P的原因是，查询轨迹的平均长度与数据库中的轨迹相似（使用D′ Q ∪ P也有类似的结果）

4.3 结果

4.3.1 mean rank

4.3.1.1 和m（P的大小）相关的结果

4.3.1.2 和downsampling rate 相关的结果

4.3.1.3 和distorting rate相关的结果

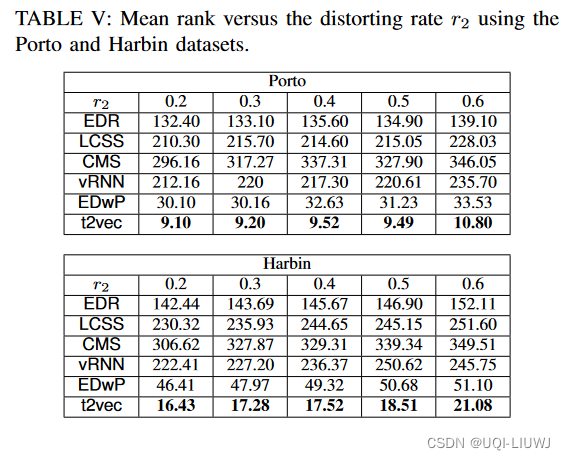
4.3.2 交叉相似性比较

一个好的相似性度量不仅应该能够识别同一基本路线的轨迹变体（自相似性），而且还应该保留两个不同轨迹之间的距离，而不考虑采样策略

计算如下：

Tb 和Tb′ 表示两个不同的原始率轨迹，Ta(r) 和Ta′(r) 是通过随机丢弃（或扭曲）样本点获得的其变体，其中丢弃（或扭曲）率为 r。

从测试数据集中随机选择10,000个轨迹对 (Tb,Tb′) 来计算它们的平均交叉距离偏差。较小的交叉距离偏差表示评估的距离非常接近真实值。

4.3.3 KNN 查询

• 随机选择1000条轨迹作为查询，从测试数据集中选择10,000条轨迹作为目标数据库
  • 应用每种方法从目标数据库中找到每个查询轨迹的k个最近邻居（k-nn）作为其基准真值
  • 接下来，根据丢弃率r1（或扭曲率r2）随机丢弃或扭曲查询和数据库轨迹的某些样本点
  • 最后，对于每个变换后的查询，我们使用每种方法从目标数据库中找到其k-nn，然后将结果与相应的基准真值进行比较
• 这种方法背后的逻辑是，一个鲁棒的距离测量应该适应非均匀和相对较低的采样率（或扭曲），并产生接近相对较高采样率（或非扭曲）的结果

4.3.4 延展性

4.3.5  网格数量的影响