小白备战大厂算法笔试(六)——堆

堆

堆是一种满足特定条件的完全二叉树，主要可分为下图所示的两种类型。

• 大顶堆：任意节点的值 ≥ 其子节点的值。
• 小顶堆：任意节点的值 ≤ 其子节点的值。

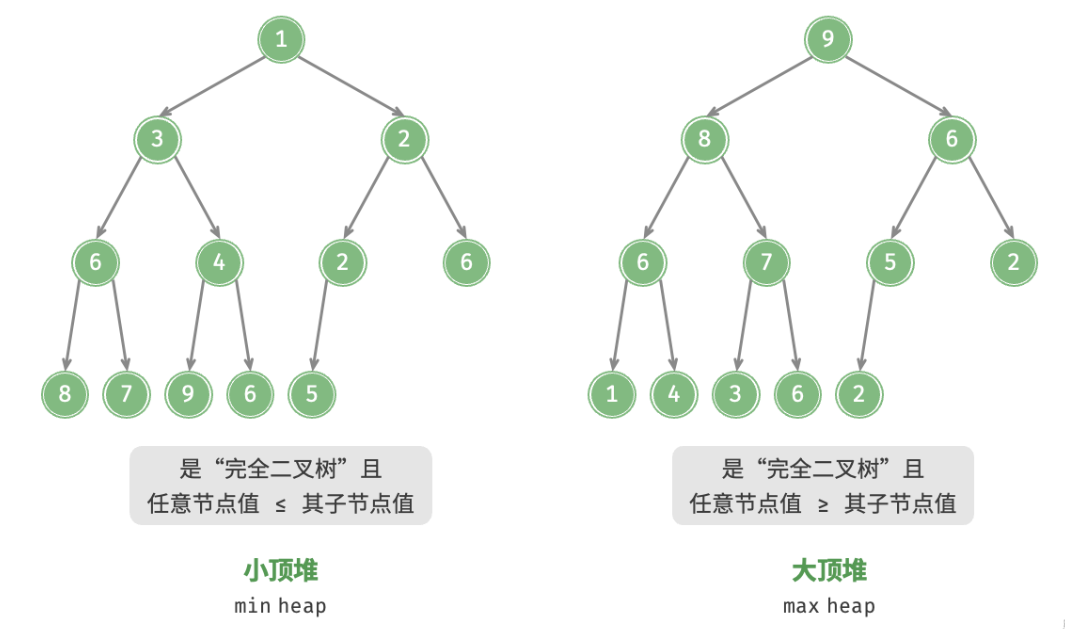
堆作为完全二叉树的一个特例，具有以下特性。

• 最底层节点靠左填充，其他层的节点都被填满。
• 我们将二叉树的根节点称为“堆顶”，将底层最靠右的节点称为“堆底”。
• 对于大顶堆（小顶堆），堆顶元素（即根节点）的值分别是最大（最小）的。

常用操作

许多编程语言提供的是优先队列，这是一种抽象数据结构，定义为具有优先级排序的队列。实际上，堆通常用作实现优先队列，大顶堆相当于元素按从大到小顺序出队的优先队列。从使用角度来看，我们可以将“优先队列”和“堆”看作等价的数据结构。

堆的常用操作见下表 ，方法名需要根据编程语言来确定。

Python：

# 初始化小顶堆
min_heap, flag = [], 1
# 初始化大顶堆
max_heap, flag = [], -1

# Python 的 heapq 模块默认实现小顶堆
# 考虑将“元素取负”后再入堆，这样就可以将大小关系颠倒，从而实现大顶堆
# 在本示例中，flag = 1 时对应小顶堆，flag = -1 时对应大顶堆

# 元素入堆
heapq.heappush(max_heap, flag * 1)
heapq.heappush(max_heap, flag * 3)
heapq.heappush(max_heap, flag * 2)
heapq.heappush(max_heap, flag * 5)
heapq.heappush(max_heap, flag * 4)

# 获取堆顶元素
peek: int = flag * max_heap[0] # 5

# 堆顶元素出堆
# 出堆元素会形成一个从大到小的序列
val = flag * heapq.heappop(max_heap) # 5
val = flag * heapq.heappop(max_heap) # 4
val = flag * heapq.heappop(max_heap) # 3
val = flag * heapq.heappop(max_heap) # 2
val = flag * heapq.heappop(max_heap) # 1

# 获取堆大小
size: int = len(max_heap)

# 判断堆是否为空
is_empty: bool = not max_heap

# 输入列表并建堆
min_heap: list[int] = [1, 3, 2, 5, 4]
heapq.heapify(min_heap)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

Go：

// Go 语言中可以通过实现 heap.Interface 来构建整数大顶堆
// 实现 heap.Interface 需要同时实现 sort.Interface
type intHeap []any

// Push heap.Interface 的方法，实现推入元素到堆
func (h *intHeap) Push(x any) {
    // Push 和 Pop 使用 pointer receiver 作为参数
    // 因为它们不仅会对切片的内容进行调整，还会修改切片的长度。
    *h = append(*h, x.(int))
}

// Pop heap.Interface 的方法，实现弹出堆顶元素
func (h *intHeap) Pop() any {
    // 待出堆元素存放在最后
    last := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return last
}

// Len sort.Interface 的方法
func (h *intHeap) Len() int {
    return len(*h)
}

// Less sort.Interface 的方法
func (h *intHeap) Less(i, j int) bool {
    // 如果实现小顶堆，则需要调整为小于号
    return (*h)[i].(int) > (*h)[j].(int)
}

// Swap sort.Interface 的方法
func (h *intHeap) Swap(i, j int) {
    (*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

// Top 获取堆顶元素
func (h *intHeap) Top() any {
    return (*h)[0]
}

/* Driver Code */
func TestHeap(t *testing.T) {
    /* 初始化堆 */
    // 初始化大顶堆
    maxHeap := &intHeap{}
    heap.Init(maxHeap)
    /* 元素入堆 */
    // 调用 heap.Interface 的方法，来添加元素
    heap.Push(maxHeap, 1)
    heap.Push(maxHeap, 3)
    heap.Push(maxHeap, 2)
    heap.Push(maxHeap, 4)
    heap.Push(maxHeap, 5)

    /* 获取堆顶元素 */
    top := maxHeap.Top()
    fmt.Printf("堆顶元素为 %d\n", top)

    /* 堆顶元素出堆 */
    // 调用 heap.Interface 的方法，来移除元素
    heap.Pop(maxHeap) // 5
    heap.Pop(maxHeap) // 4
    heap.Pop(maxHeap) // 3
    heap.Pop(maxHeap) // 2
    heap.Pop(maxHeap) // 1

    /* 获取堆大小 */
    size := len(*maxHeap)
    fmt.Printf("堆元素数量为 %d\n", size)

    /* 判断堆是否为空 */
    isEmpty := len(*maxHeap) == 0
    fmt.Printf("堆是否为空 %t\n", isEmpty)
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

堆的实现

下文实现的是大顶堆。若要将其转换为小顶堆，只需将所有大小逻辑判断取逆（例如，将 ≥ 替换为 ≤ ）。

存储与表示

完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树，将采用数组来存储堆。当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。

如下图所示，给定索引i ，其左子节点索引为 2i+1 ，右子节点索引为 2i+2 ，父节点索引为 (i−1)/2（向下取整）。当索引越界时，表示空节点或节点不存在。

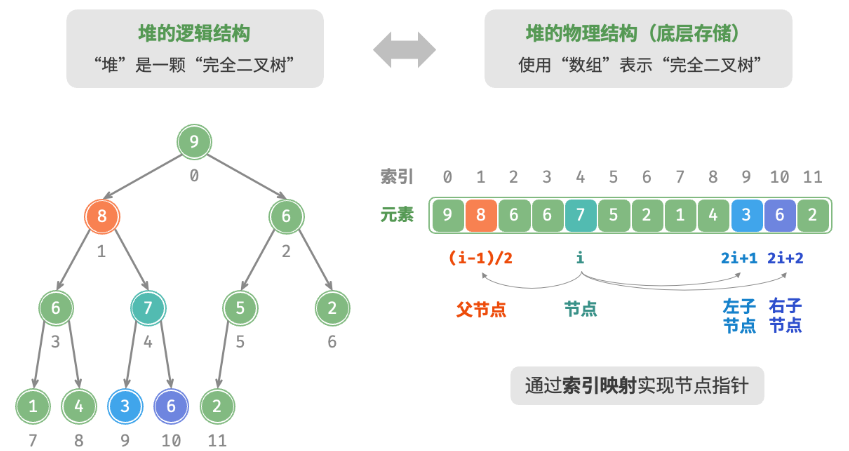
将索引映射公式封装成函数，方便后续使用。

Python：

def left(self, i: int) -> int:
    """获取左子节点索引"""
    return 2 * i + 1

def right(self, i: int) -> int:
    """获取右子节点索引"""
    return 2 * i + 2

def parent(self, i: int) -> int:
    """获取父节点索引"""
    return (i - 1) // 2  # 向下整除
1
2
3
4
5
6
7
8
9
10
11

Go：

/* 获取左子节点索引 */
func (h *maxHeap) left(i int) int {
    return 2*i + 1
}

/* 获取右子节点索引 */
func (h *maxHeap) right(i int) int {
    return 2*i + 2
}

/* 获取父节点索引 */
func (h *maxHeap) parent(i int) int {
    // 向下整除
    return (i - 1) / 2
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

访问堆顶元素

堆顶元素即为二叉树的根节点，也就是列表的首个元素。

Python：

def peek(self) -> int:
    """访问堆顶元素"""
    return self.max_heap[0]
1
2
3

Go：

/* 访问堆顶元素 */
func (h *maxHeap) peek() any {
    return h.data[0]
}
1
2
3
4

元素入堆

给定元素 val ，首先将其添加到堆底。添加之后，由于 val 可*其他元素，堆的成立条件可能已被破坏。因此，需要修复从插入节点到根节点的路径上的各个节点，这个操作被称为堆化。考虑从入堆节点开始，从底至顶执行堆化。如下图所示，我们比较插入节点与其父节点的值，如果插入节点更大，则将它们交换。然后继续执行此操作，从底至顶修复堆中的各个节点，直至越过根节点或遇到无须交换的节点时结束。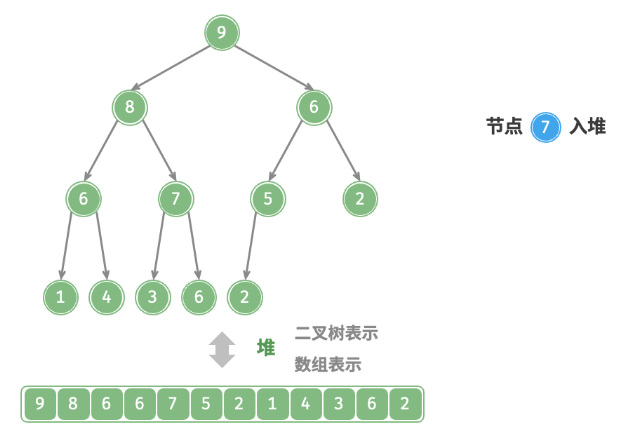

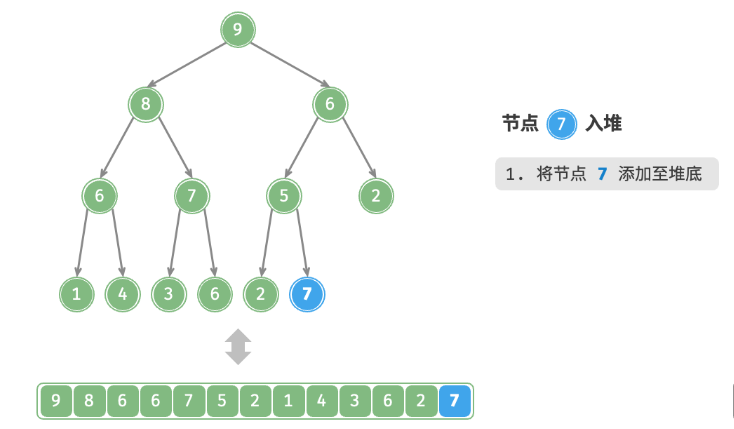
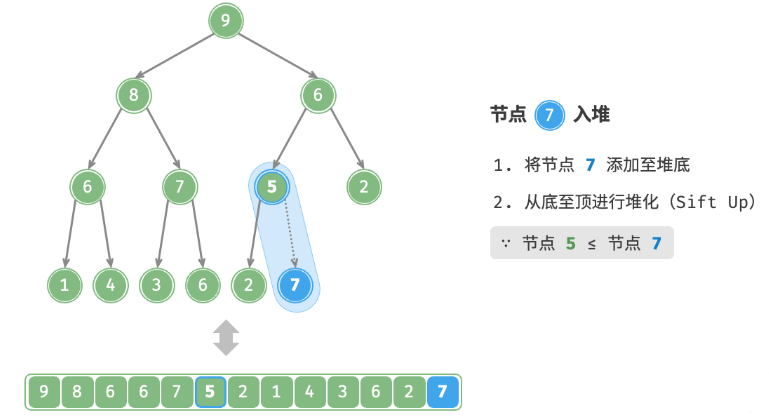
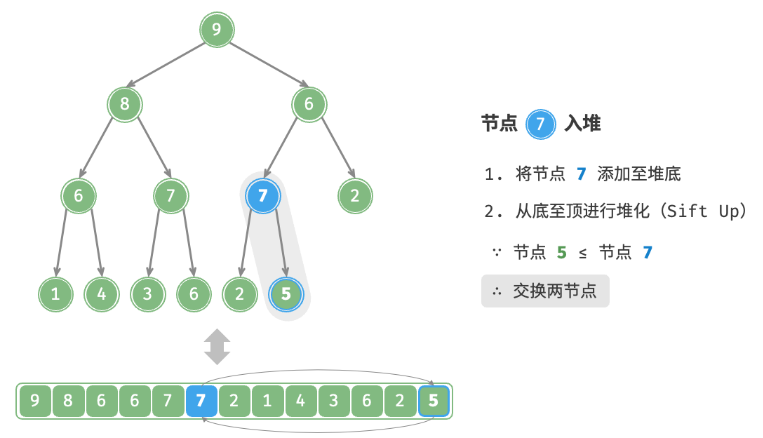
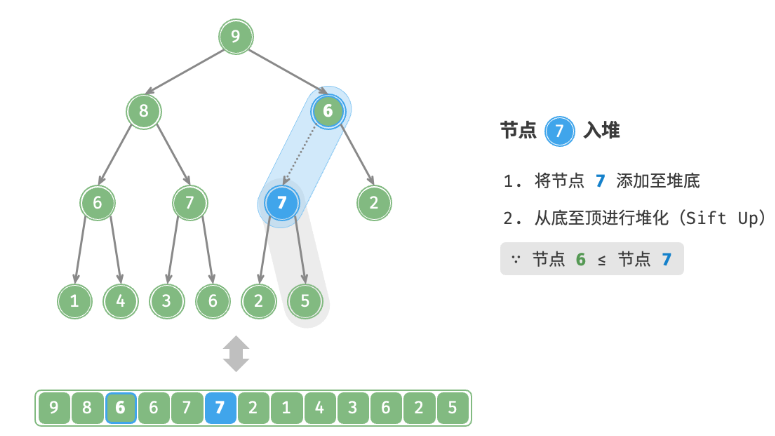
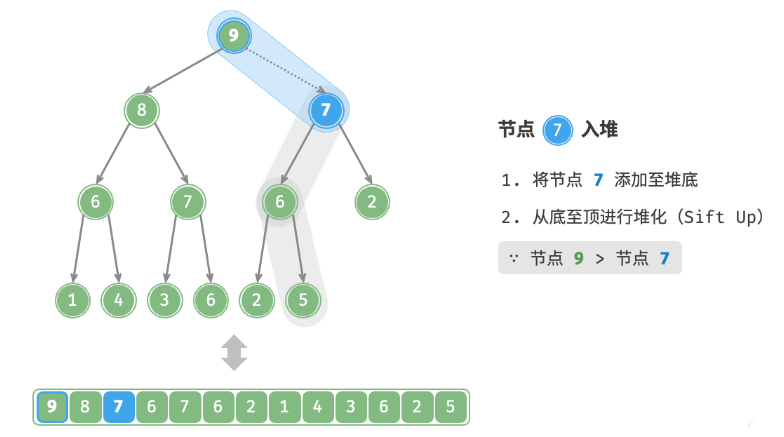
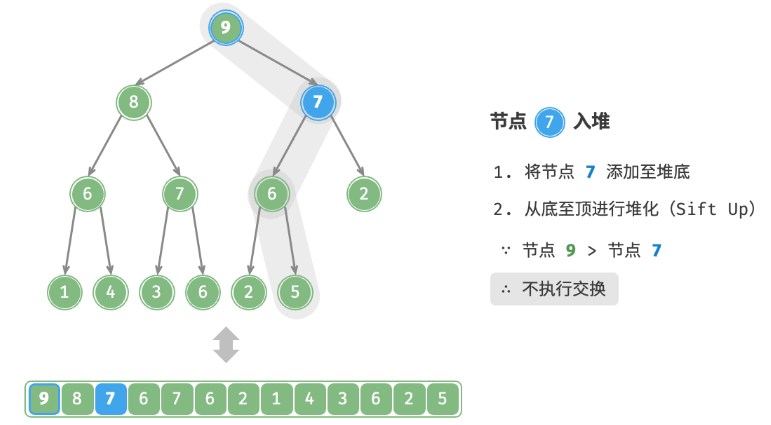
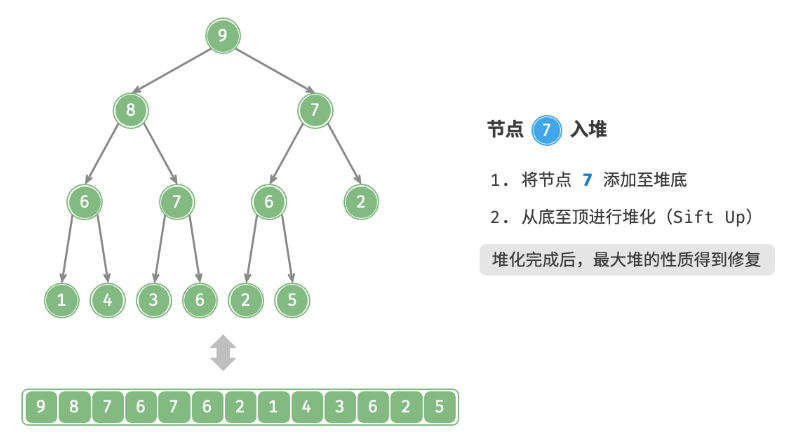
设节点总数为n ，则树的高度为 n(log⁡n) 。由此可知，堆化操作的循环轮数最多为 O(log⁡n) ，元素入堆操作的时间复杂度为 O(log⁡n) 。

Python：

def push(self, val: int):
    """元素入堆"""
    # 添加节点
    self.max_heap.append(val)
    # 从底至顶堆化
    self.sift_up(self.size() - 1)

def sift_up(self, i: int):
    """从节点 i 开始，从底至顶堆化"""
    while True:
        # 获取节点 i 的父节点
        p = self.parent(i)
        # 当“越过根节点”或“节点无须修复”时，结束堆化
        if p < 0 or self.max_heap[i] <= self.max_heap[p]:
            break
        # 交换两节点
        self.swap(i, p)
        # 循环向上堆化
        i = p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Go：

/* 元素入堆 */
func (h *maxHeap) push(val any) {
    // 添加节点
    h.data = append(h.data, val)
    // 从底至顶堆化
    h.siftUp(len(h.data) - 1)
}

/* 从节点 i 开始，从底至顶堆化 */
func (h *maxHeap) siftUp(i int) {
    for true {
        // 获取节点 i 的父节点
        p := h.parent(i)
        // 当“越过根节点”或“节点无须修复”时，结束堆化
        if p < 0 || h.data[i].(int) <= h.data[p].(int) {
            break
        }
        // 交换两节点
        h.swap(i, p)
        // 循环向上堆化
        i = p
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

元素出堆

堆顶元素是二叉树的根节点，即列表首元素。如果我们直接从列表中删除首元素，那么二叉树中所有节点的索引都会发生变化，这将使得后续使用堆化修复变得困难。为了尽量减少元素索引的变动，采用以下操作步骤：

1. 交换堆顶元素与堆底元素（即交换根节点与最右叶节点）。
2. 交换完成后，将堆底从列表中删除（注意，由于已经交换，实际上删除的是原来的堆顶元素）。
3. 从根节点开始，从顶至底执行堆化。

如下图所示，“从顶至底堆化”的操作方向与“从底至顶堆化”相反，我们将根节点的值与其两个子节点的值进行比较，将最大的子节点与根节点交换。然后循环执行此操作，直到越过叶节点或遇到无须交换的节点时结束。

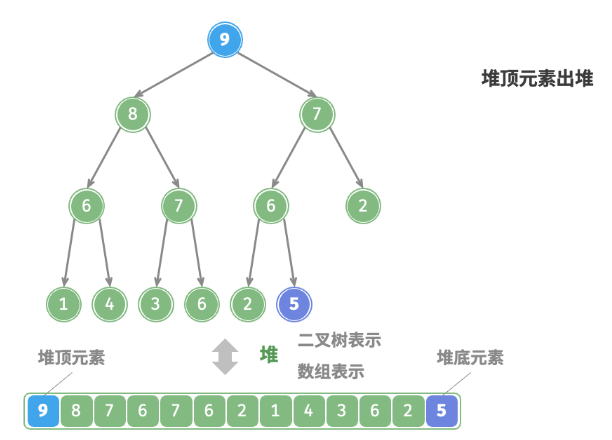
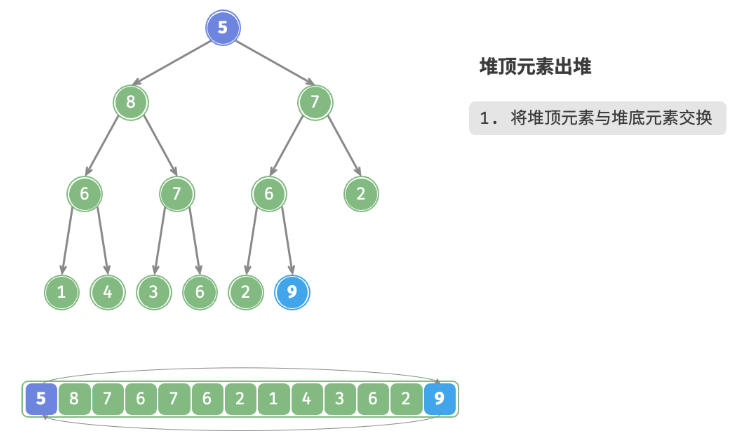
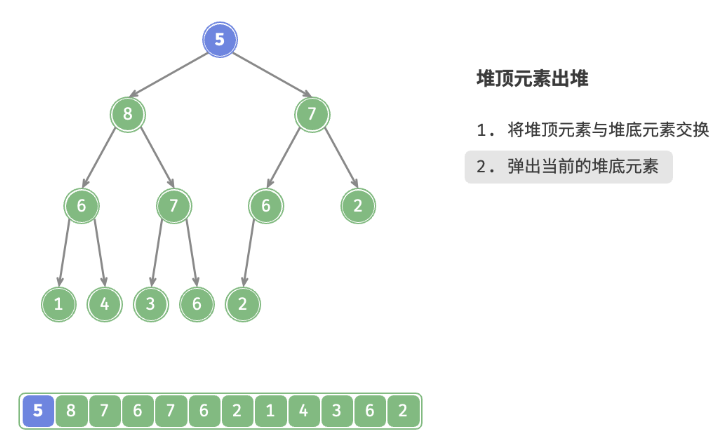
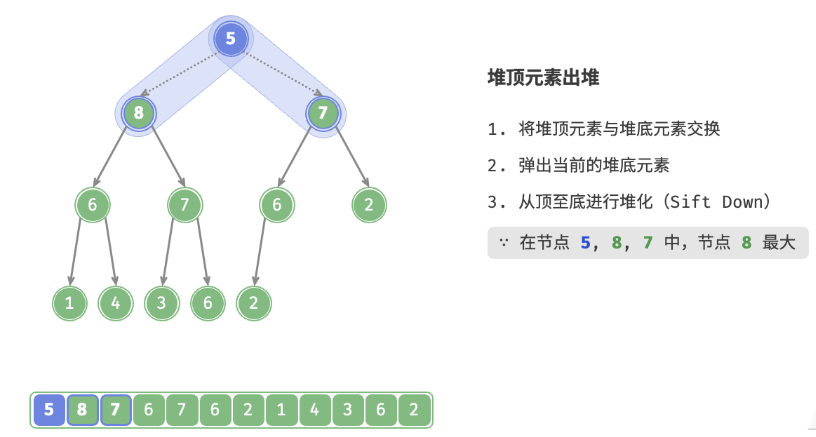
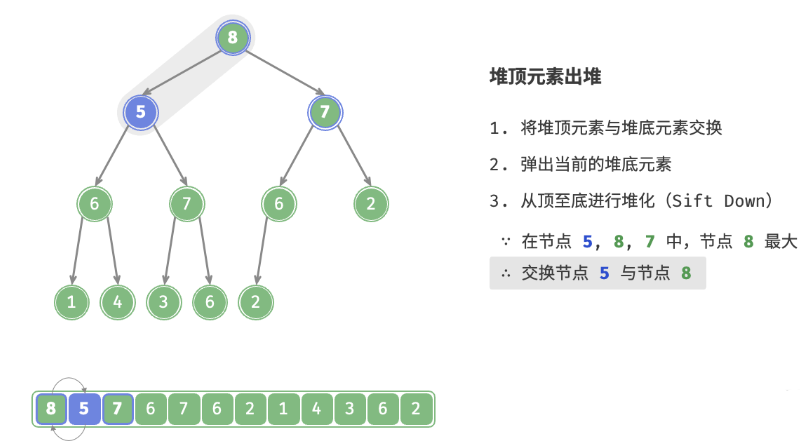
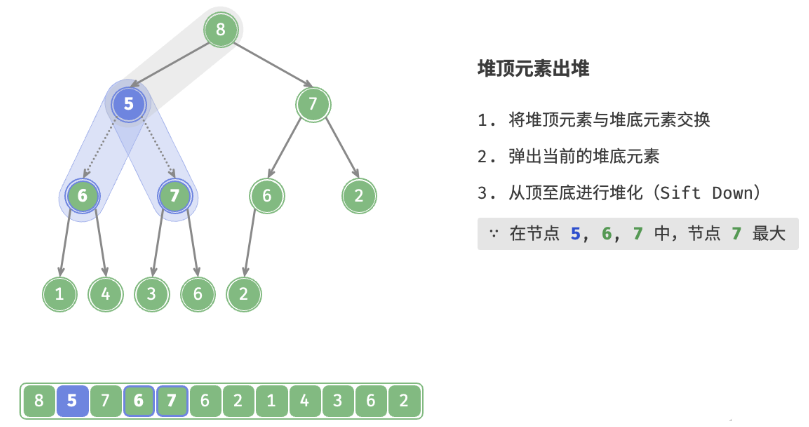
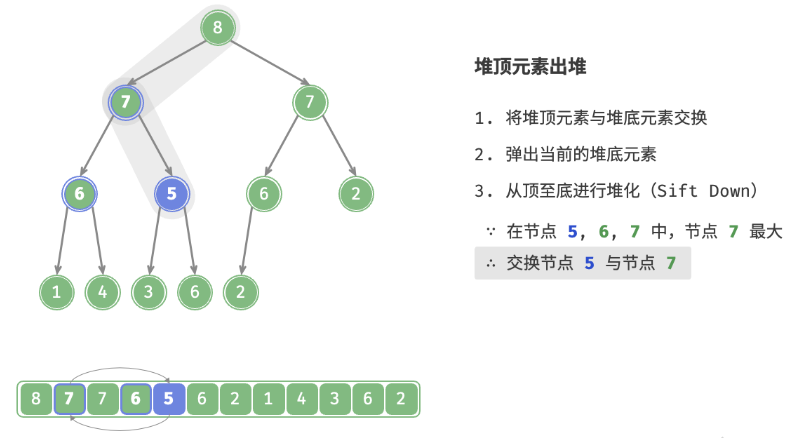
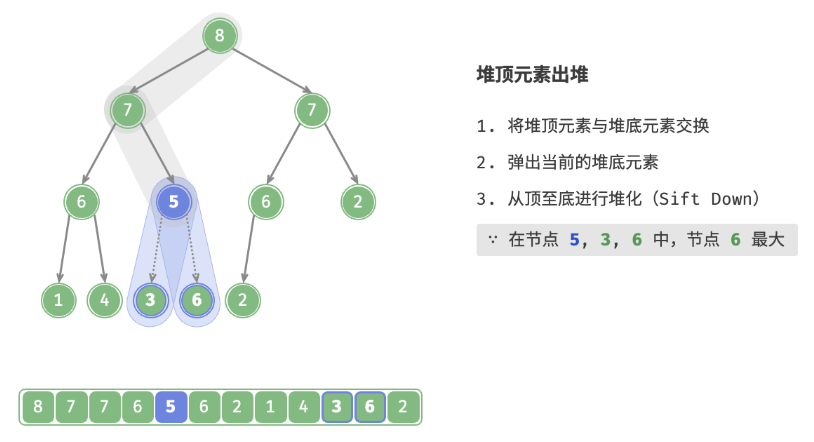
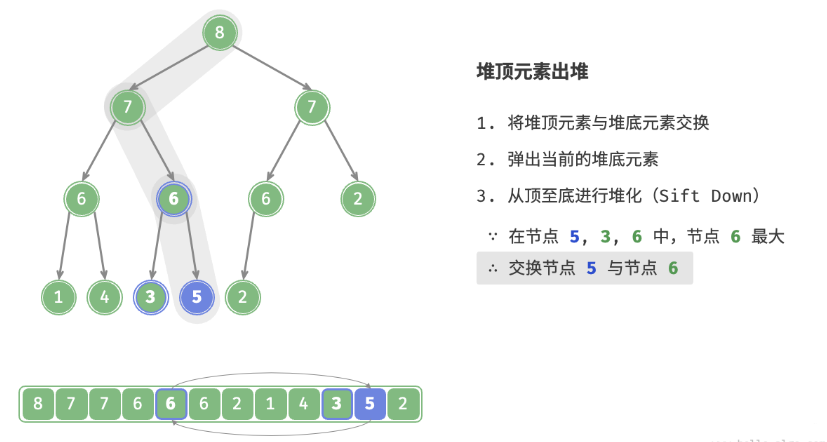
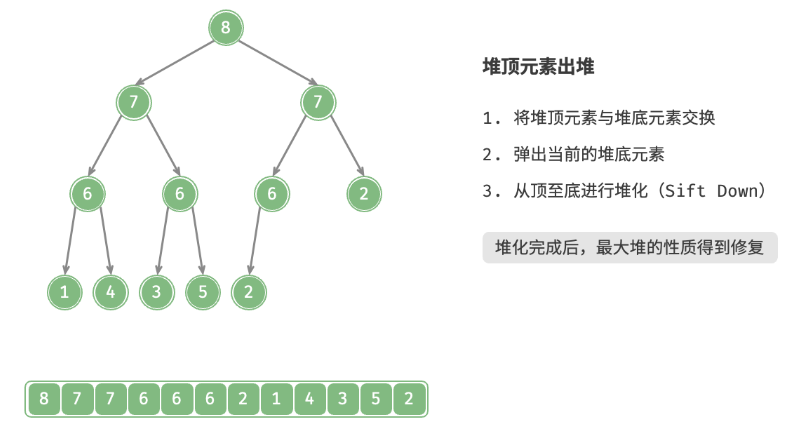
与元素入堆操作相似，堆顶元素出堆操作的时间复杂度也为O(log⁡n) 。

Python：

def pop(self) -> int:
    """元素出堆"""
    # 判空处理
    if self.is_empty():
        raise IndexError("堆为空")
    # 交换根节点与最右叶节点（即交换首元素与尾元素）
    self.swap(0, self.size() - 1)
    # 删除节点
    val = self.max_heap.pop()
    # 从顶至底堆化
    self.sift_down(0)
    # 返回堆顶元素
    return val

def sift_down(self, i: int):
    """从节点 i 开始，从顶至底堆化"""
    while True:
        # 判断节点 i, l, r 中值最大的节点，记为 ma
        l, r, ma = self.left(i), self.right(i), i
        if l < self.size() and self.max_heap[l] > self.max_heap[ma]:
            ma = l
        if r < self.size() and self.max_heap[r] > self.max_heap[ma]:
            ma = r
        # 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if ma == i:
            break
        # 交换两节点
        self.swap(i, ma)
        # 循环向下堆化
        i = ma
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Go：

/* 元素出堆 */
func (h *maxHeap) pop() any {
    // 判空处理
    if h.isEmpty() {
        fmt.Println("error")
        return nil
    }
    // 交换根节点与最右叶节点（即交换首元素与尾元素）
    h.swap(0, h.size()-1)
    // 删除节点
    val := h.data[len(h.data)-1]
    h.data = h.data[:len(h.data)-1]
    // 从顶至底堆化
    h.siftDown(0)

    // 返回堆顶元素
    return val
}

/* 从节点 i 开始，从顶至底堆化 */
func (h *maxHeap) siftDown(i int) {
    for true {
        // 判断节点 i, l, r 中值最大的节点，记为 max
        l, r, max := h.left(i), h.right(i), i
        if l < h.size() && h.data[l].(int) > h.data[max].(int) {
            max = l
        }
        if r < h.size() && h.data[r].(int) > h.data[max].(int) {
            max = r
        }
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if max == i {
            break
        }
        // 交换两节点
        h.swap(i, max)
        // 循环向下堆化
        i = max
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

常见应用

• 优先队列：堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为 O(log⁡n) ，而建队操作为 O(n) ，这些操作都非常高效。
• 堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。在后续写排序的文章会讲到。
• 获取最大的k个元素：这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

建堆操作

在某些情况下，我们希望使用一个列表的所有元素来构建一个堆，这个过程被称为“建堆操作”。

自上而下构建

我们首先创建一个空堆，然后遍历列表，依次对每个元素执行“入堆操作”，即先将元素添加至堆的尾部，再对该元素执行“从底至顶”堆化。

每当一个元素入堆，堆的长度就加一，因此堆是“自上而下”地构建的。

设元素数量为n，每个元素的入堆操作使用O(log⁡n) 时间，因此该建堆方法的时间复杂度为 O(nlog⁡n) 。

自下而上构建

实际上，可以实现一种更为高效的建堆方法，共分为两步。

1. 将列表所有元素原封不动添加到堆中。
2. 倒序遍历堆（即层序遍历的倒序），依次对每个非叶节点执行“从顶至底堆化”。

在倒序遍历中，堆是“自下而上”地构建的，需要重点理解以下两点。

• 由于叶节点没有子节点，因此无需对它们执行堆化。最后一个节点的父节点是最后一个非叶节点。
• 在倒序遍历中，我们能够保证当前节点之下的子树已经完成堆化（已经是合法的堆），而这是堆化当前节点的前置条件。

Python：

def __init__(self, nums: list[int]):
    """构造方法，根据输入列表建堆"""
    # 将列表元素原封不动添加进堆
    self.max_heap = nums
    # 堆化除叶节点以外的其他所有节点
    for i in range(self.parent(self.size() - 1), -1, -1):
        self.sift_down(i)
1
2
3
4
5
6
7

Go：

/* 构造函数，根据切片建堆 */
func newMaxHeap(nums []any) *maxHeap {
    // 将列表元素原封不动添加进堆
    h := &maxHeap{data: nums}
    for i := h.parent(len(h.data) - 1); i >= 0; i-- {
        // 堆化除叶节点以外的其他所有节点
        h.siftDown(i)
    }
    return h
}
1
2
3
4
5
6
7
8
9
10

经过某种复杂的推算表明，输入列表并建堆的时间复杂度为O(n) ，非常高效。也就是说自下而上的构建效率高于自上而下的构建效率。

TOP-K问题

Question：

给定一个长度为n无序数组 nums ，请返回数组中前k大的元素。

对于该问题，介绍两种思路比较直接的解法，再介绍效率更高的堆解法。

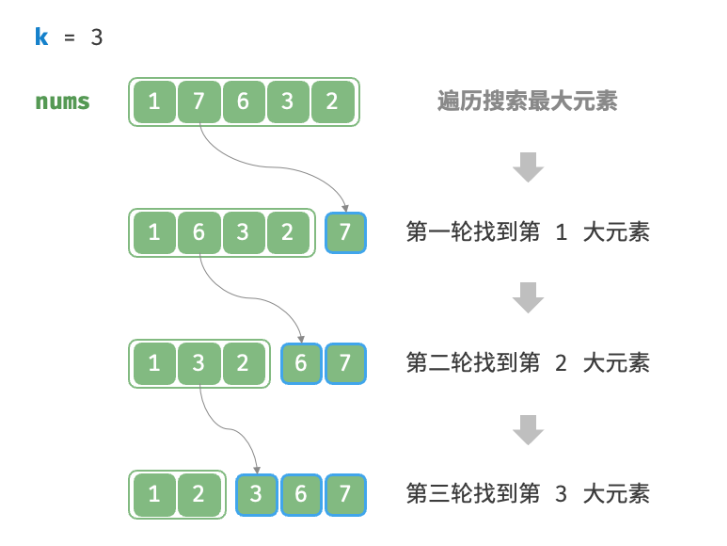
遍历选择

可以进行下图所示的k轮遍历，分别在每轮中提取第 1、2、…、k 大的元素，时间复杂度为O(nk)。此方法只适用于k≪n的情况，因为当k与n比较接近时，其时间复杂度趋向于 O(n^2) ，非常耗时。

Python：

def findKthLargest(nums, k):
    result = []
    for i in range(k):
        max_num = max(nums)
        result.append(max_num)
        nums.remove(max_num)
    return result
1
2
3
4
5
6
7

Go：

func findKthLargest(nums []int, k int) []int {
	result := make([]int, k)
	for i := 0; i < k; i++ {
		max := nums[0]
		index := 0
		for i, num := range nums {
			if num > max {
				max = num
				index = i
			}
		}
		result[i] = max
		nums = append(nums[:index], nums[index+1:]...)
	}
	return result
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

当 k=n 时，可以得到完整的有序序列，此时等价于“选择排序”算法。

排序

我们可以先对数组 nums 进行排序，再返回最右边的k个元素，时间复杂度为 O(nlog⁡n) 。显然，该方法“超额”完成任务了，因为我们只需要找出最大的k个元素即可，而不需要排序其他元素。

Python：

def findKthLargest(nums, k):
    nums.sort(reverse=True)
    return nums[:k]
1
2
3

Go：

func findKthLargest(nums []int, k int) []int {
	sort.Sort(sort.Reverse(sort.IntSlice(nums)))
	return nums[:k]
}

//或者
func findKthLargest(nums []int, k int) []int {
	sort.Slice(nums, func(i, j int) bool {
		return nums[i] > nums[j]
	})
	return nums[:k]
}
1
2
3
4
5
6
7
8
9
10
11
12

堆

我们可以基于堆更加高效地解决 Top-K 问题：

1. 初始化一个小顶堆，其堆顶元素最小。
2. 先将数组的前k个元素依次入堆。
3. 从第k+1 个元素开始，若当前元素大于堆顶元素，则将堆顶元素出堆，并将当前元素入堆。
4. 遍历完成后，堆中保存的就是最大的k个元素。

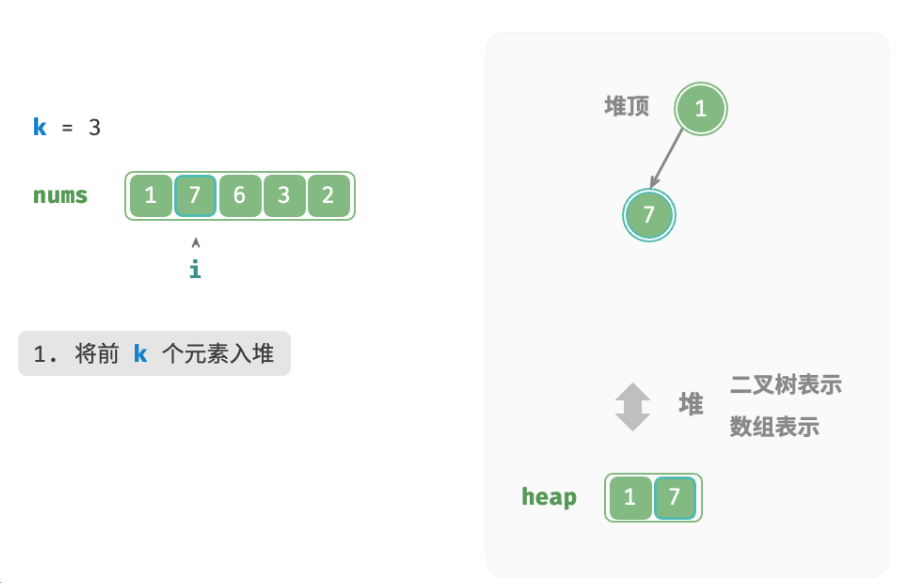
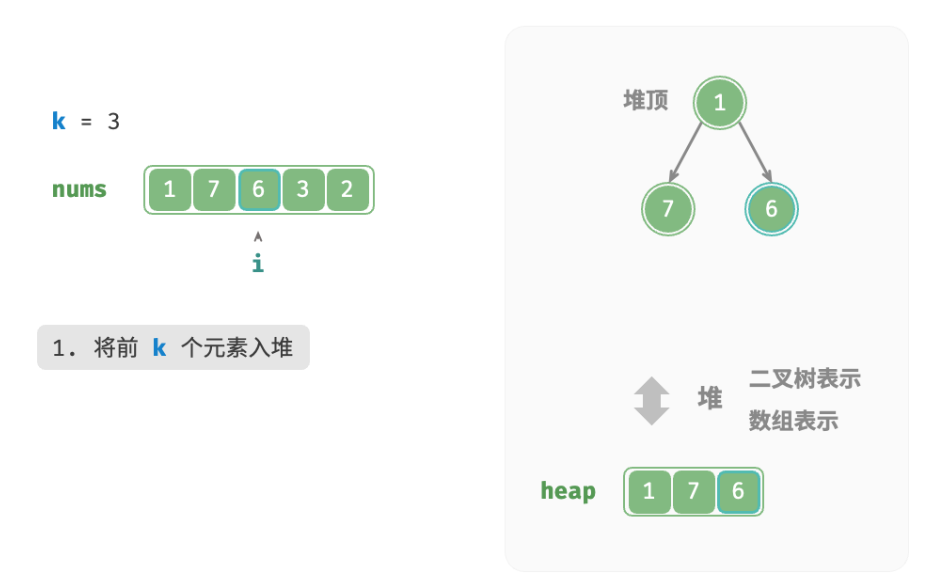
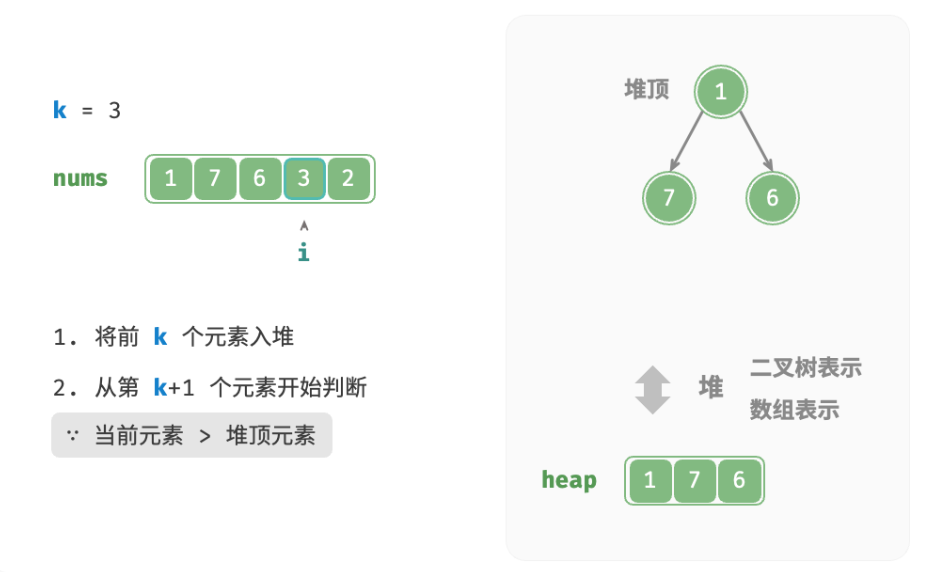
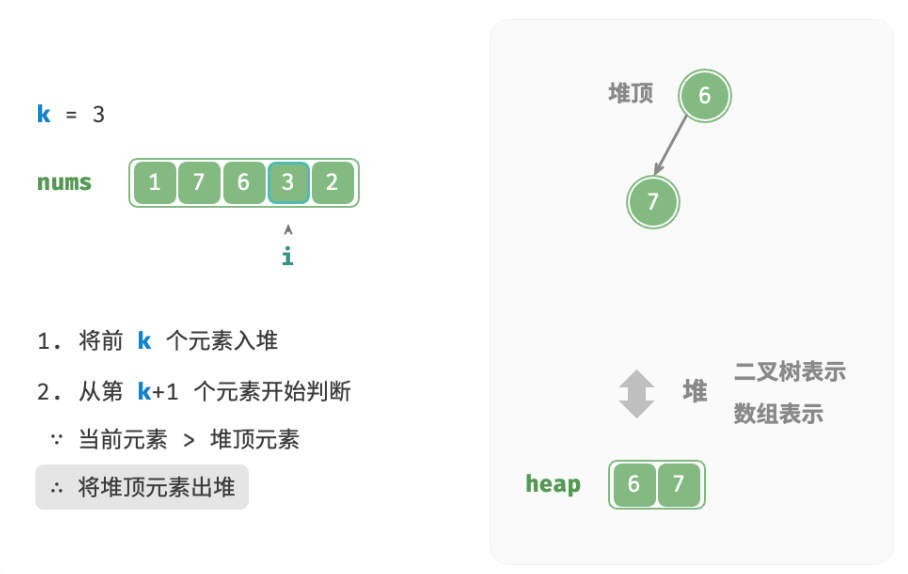
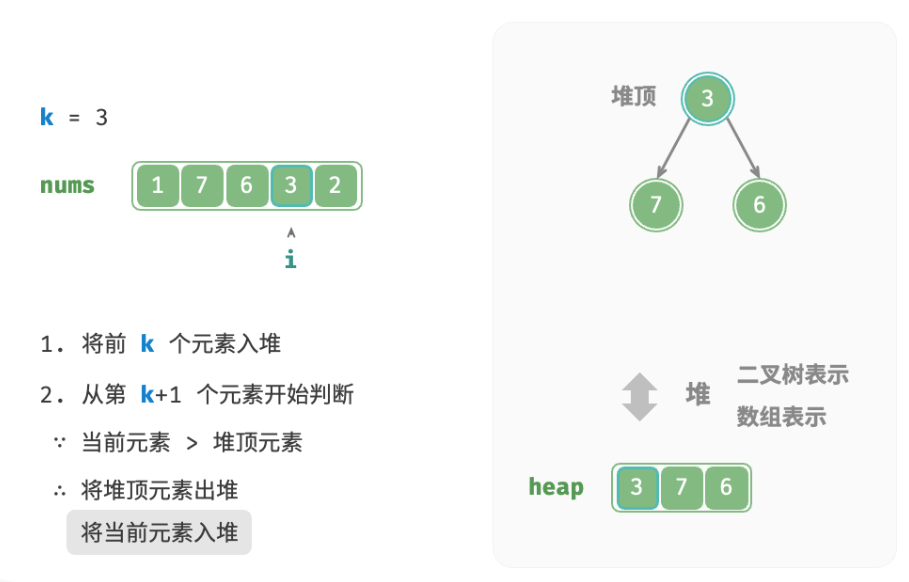
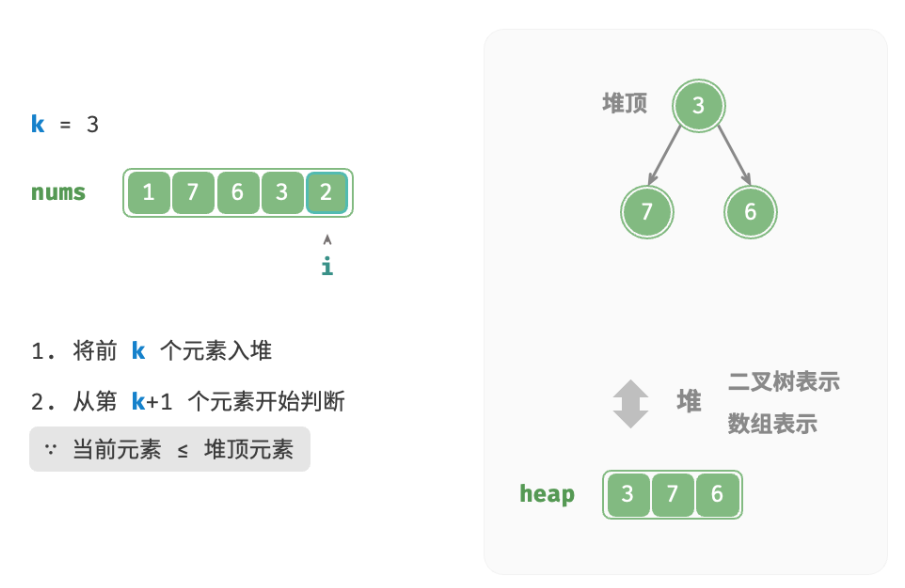
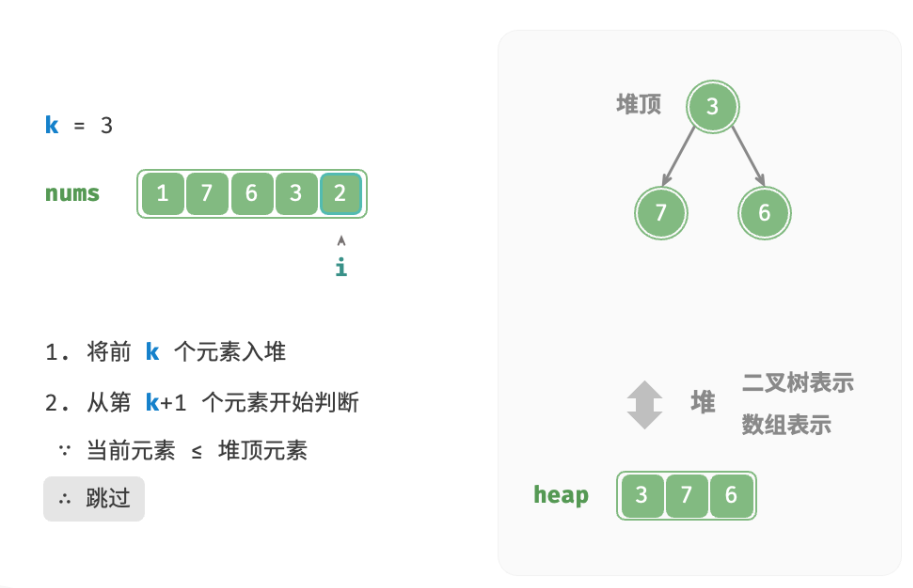
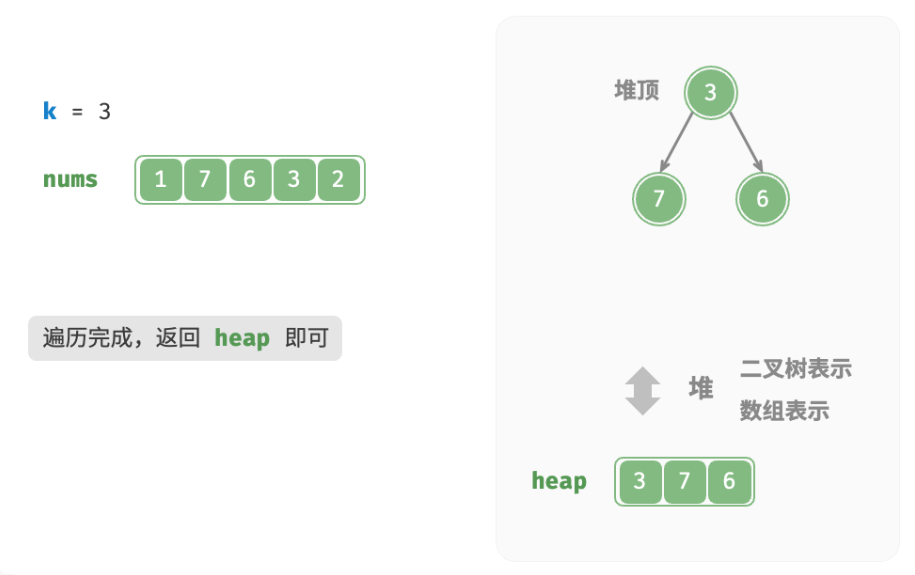
总共执行了n轮入堆和出堆，堆的最大长度为k，因此时间复杂度为 O(nlog⁡k) 。该方法的效率很高，当 k 较小时，时间复杂度趋向 O(n) ；当 k 较大时，时间复杂度不会超过 O(nlog⁡n) 。另外，该方法适用于动态数据流的使用场景。在不断加入数据时，可以持续维护堆内的元素，从而实现最大k个元素的动态更新。

Python：

def top_k_heap(nums: list[int], k: int) -> list[int]:
    """基于堆查找数组中最大的 k 个元素"""
    heap = []
    # 将数组的前 k 个元素入堆
    for i in range(k):
        heapq.heappush(heap, nums[i])
    # 从第 k+1 个元素开始，保持堆的长度为 k
    for i in range(k, len(nums)):
        # 若当前元素大于堆顶元素，则将堆顶元素出堆、当前元素入堆
        if nums[i] > heap[0]:
            heapq.heappop(heap)
            heapq.heappush(heap, nums[i])
    return heap
1
2
3
4
5
6
7
8
9
10
11
12
13

Go：

/* 基于堆查找数组中最大的 k 个元素 */
func topKHeap(nums []int, k int) *minHeap {
    h := &minHeap{}
    heap.Init(h)
    // 将数组的前 k 个元素入堆
    for i := 0; i < k; i++ {
        heap.Push(h, nums[i])
    }
    // 从第 k+1 个元素开始，保持堆的长度为 k
    for i := k; i < len(nums); i++ {
        // 若当前元素大于堆顶元素，则将堆顶元素出堆、当前元素入堆
        if nums[i] > h.Top().(int) {
            heap.Pop(h)
            heap.Push(h, nums[i])
        }
    }
    return h
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

References：https://www.hello-algo.com/chapter_heap/