-
GLSL ES着色器语言 使用矢量和矩阵的相关规范
目录
GLSL ES支持矢量和矩阵类型,这两种数据类型很适合用来处理计算机图形。矢量和矩阵类型的变量都包含多个元素,每个元素是一个数值(整型数、浮点数或布尔值)。矢量将这些元素排成一列,可以用来表示顶点坐标或颜色值等,而矩阵则将元素划分成行和列,可以用来表示变换矩阵。下图给出了矢量和矩阵的例子。
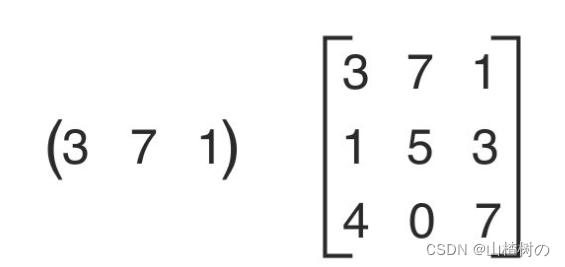
矢量和矩阵类型

下面是声明矢量和矩阵的例子:


赋值和构造
我们使用等号(=)来对矢量和矩阵进行赋值操作。记住,赋值运算符左右两边的变量/值的类型必须一致,左右两边的(矢量或矩阵的)元素个数也必须相同。比如说,下面这行代码就会出错。
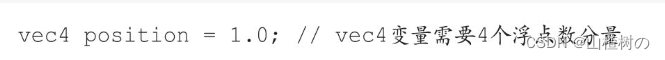
这里,vec4类型变量有4个元素,你应当以某种方式传入4个浮点数值。通常我们使用与数据类型同名的内置构造函数来生成变量,对于vec4类型来说,就可以使用内置的vec4()函数。比如,如果要创建4个分量各是1.0、2.0、3.0和4.0的vec4类型变量,你就可以像下面这样调用vec4()函数。
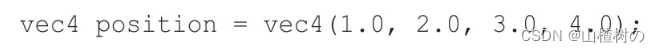
这种专门创建指定类型的变量的函数被称为构造函数(constructor functions),构造函数的名称和其创建的变量的类型名称总是一致的。
矢量构造函数
在GLSL ES中,矢量非常重要,所以GLSL ES提供了丰富灵活的方式来创建矢量。比如:

在第2行代码中,构造函数忽略了v3的第3个分量,只用其第1个和第2个分量创建了一个新的变量。类似地,在第3行代码中,只向构造函数中传入了一个参数1.0,构造函数就会自动地将这个参数值赋给新建矢量的所有元素。但是,如果构造函数接收了不止1个参数,但是参数的个数又比矢量的元素个数少,那么就会出错。
最后,也可以将多个矢量组合成一个矢量,比如:
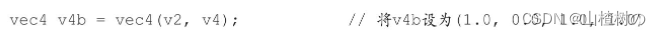
这里的规则是,先把第1个参数v2的所有元素填充进来,如果还未填满,就继续用第2个参数v4中的元素填充。
矩阵构造函数
矩阵构造函数的使用方式与矢量构造函数的使用方式很类似。但是,你要保证存储在矩阵中的元素是按照列主序排列的。下面几个例子显示了使用矩阵构造函数的不同方式。
构造矩阵的几种方式
● 向矩阵构造函数中传入矩阵的每一个元素的数值来构造矩阵,注意传入值的顺序必须是列主序的。

● 向矩阵构造函数中传入一个或多个矢量,按照列主序使用矢量里的元素值来构造矩阵。

● 向矩阵构造函数中传入矢量和数值,按照列主序使用矢量里的元素值和直接传入的数值来构造矩阵。

● 向矩阵构造函数中传入单个数值,这样将生成一个对角线上元素都是该数值,其他元素为0.0的矩阵。

与矢量构造函数类似,如果传入的数值的数量大于1,又没有达到矩阵元素的数量,就会出错。
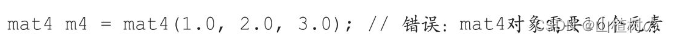
访问元素
为了访问矢量或矩阵中的元素,可以使用.或[]运算符,下面将分节叙述。
. 运算符
在矢量变量名后接点运算符(.),然后接上分量名,就可以访问矢量的元素了。矢量的分量名如下表所示。
矢量的分量名

由于矢量可以用来存储顶点的坐标、颜色和纹理坐标,所以GLSL ES支持以上三种分量名称以增强程序的可读性。事实上,任何矢量的x、r或s分量都会返回第1个分量,y、g、t分量都返回第2个分量,等等。如果你愿意,你可以随意地交换使用它们。比如:

如你所见,在这些例子中,x、r和s虽然名称不同,但访问的却都是第1个分量。如果试图访问超过矢量长度的分量,就会出错:

将(同一个集合的)多个分量名共同置于点运算符后,就可以从矢量中同时抽取出多个分量。这个过程称作混合(swizzling)。在下面这个例子中,我们使用了x、y、z和w,其他的集合也有相同的效果:


聚合分量名也可以用来作为赋值表达式(=)的左值:

记住,此时的多个分量名必须属于同一个集合,比如说,你不能使用v3.was。
[ ]运算符
除了.运算符,还可以使用[]运算符并通过数组下标来访问矢量或矩阵的元素。注意,矩阵中的元素仍然是按照列主序读取的。与在JavaScript中一样,下标从0开始,所以通过[0]可以访问到矩阵中的第1列元素,[1]可以访问到第2列元素,[2]可以访问到第3列元素,等等,如下所示:
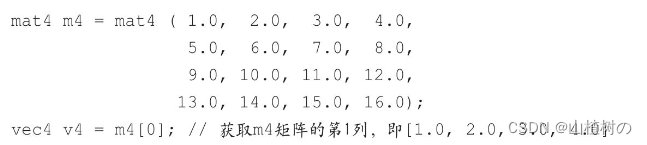
此外,连续使用两个[]运算符可以访问某列的某个元素:

同样,你也可以同时使用[]运算符和分量名来访问矩阵中的元素,如下所示:
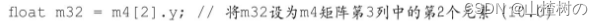
这里有一个限制,那就是在[]中只能出现的索引值必须是常量索引值(constant index),常量索引值的定义如下:
● 整型字面量(如0或1)。
● 用const修饰的全局变量或局部变量,不包括函数参数。
● 循环索引。
● 由前述三条中的项组成的表达式。
下面这个例子就用到了const变量作为访问数组元素的索引:

下面这个例子用到了const组成的表达式作为索引:
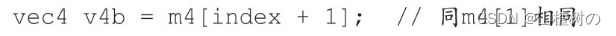
注意,你不能使用未经const修饰的变量作为索引值,因为它不是一个常量索引值(除非它是循环索引):

运算符
下表显示了矢量和矩阵所支持的运算。矩阵和矢量的运算符与基本类型(比如整数)的运算符很类似。注意,对于矢量和矩阵,只可以使用比较运算符中的==和!=,不可以使用>、<、>=和<=。如果你想比较矢量和矩阵的大小,应该使用内置函数,比如lessThan()。
矢量和矩阵可用的运算符
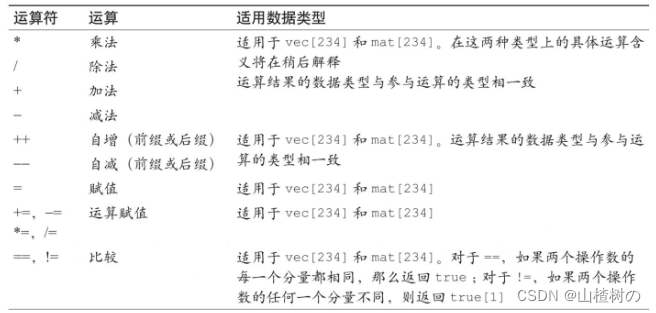
注意,当运算赋值操作作用于矢量或矩阵时,实际上是逐分量地对矩阵或矢量的每一个元素进行独立的运算赋值。
矢量和矩阵相关运算
下面这些例子显示了矢量和矩阵在运算时的常见情形。我们假设,在这些例子中,变量是如下定义的:

矢量和浮点数的运算
这个例子显示了+操作符的作用:

例如,v3a=vec3(1.0,2.0,3.0)而f=1.0,那么结果就是v3b=(2.0,3.0,4.0)。
矢量运算
矢量运算操作发生在矢量的每个分量上。

例如,v3a=vec3(1.0,2.0,3.0)而v3b=(4.0,5.0,6.0),那么结果就是v3c=(5.0,7.0,9.0)。
矩阵和浮点数的运算
矩阵与浮点数的运算发生在矩阵的每个分量上。

矩阵右乘矢量
矩阵右乘矢量的结果是矢量,其中每个分量都是原矢量中的对应分量,乘上矩阵对应行的每个元素的积的加和。
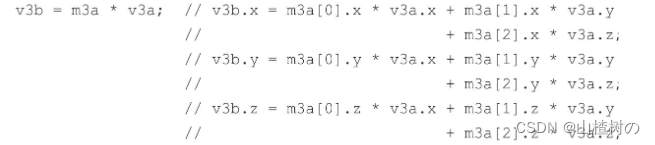
矩阵左乘矢量

矩阵与矩阵相乘

-
相关阅读:
Linux 忘记root密码解决方法(CentOS7.9)
10.20作业
如何配置Log4j以便将日志信息输出到文件,并指定日志文件的格式?请解释Log4j中的PatternLayout,并给出一个常用的日志格式模式。
git gitlab撤回已经提交的代码,回滚到某一个版本/节点
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(十六)
云计算面试题【后期】
vue或webpack加载highcharts与highcharts-3d
【微信小程序】网络请求
Java理论题(2)——简答题
深聊全链路压测之:第二十四讲 | 分布式调度平台的选型与落地。
- 原文地址:https://blog.csdn.net/dabaooooq/article/details/132793809