并查集快速合并

对于一组数据，并查集主要支持两个动作：

• union(p,q) - 将 p 和 q 两个元素连接起来。

• find(p) - 查询 p 元素在哪个集合中。

• isConnected(p,q) - 查看 p 和 q 两个元素是否相连接在一起。

在上一小节中，我们用 id 数组的形式表示并查集，实际操作过程中查找的时间复杂度为 O(1)，但连接效率并不高。

本小节，我们将用另外一种方式实现并查集。把每一个元素，看做是一个节点并且指向自己的父节点，根节点指向自己。如下图所示，节点 3 指向节点 2，代表 3 和 2 是连接在一起的，节点2本身是根节点，所以指向自己。

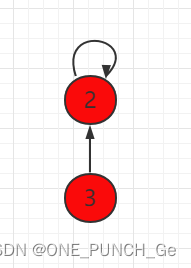
同样用数组表示并查集，但是下面一组元素用 parent 表示当前元素指向的父节点，每个元素指向自己，都是独立的。

如果此时操作 union(4,3)，将元素 4 指向元素 3：

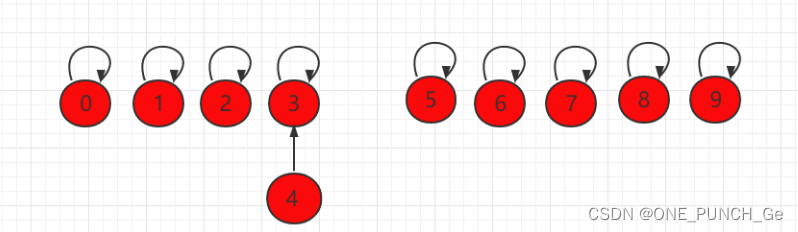
数组也进行相应改变：

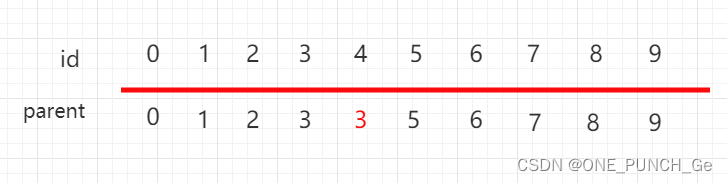
判断两个元素是否连接，只需要判断根节点是否相同即可。

如下图，节点 4 和节点 9 的根节点都是 8，所以它们是相连的。

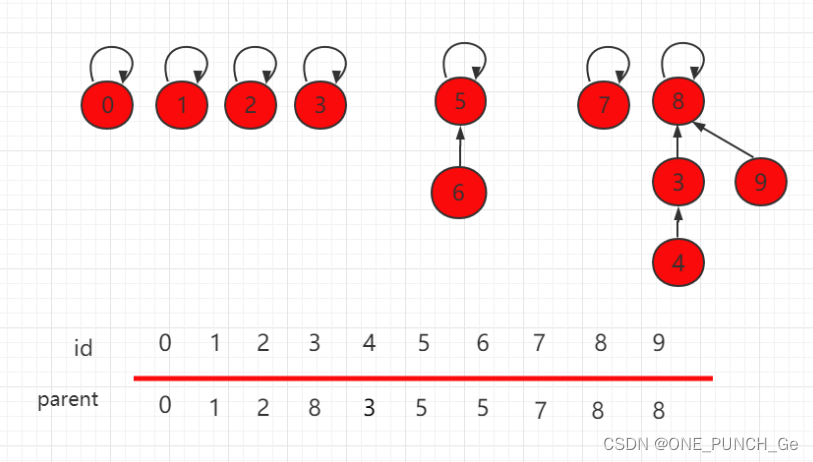
连接两个元素，只需要找到它们对应的根节点，使根节点相连，那它们就是相连的节点。

假设要使上图中的 6 和 4 相连，只需要把 6 的根节点 5 指向 4 的根节点 8 即可。

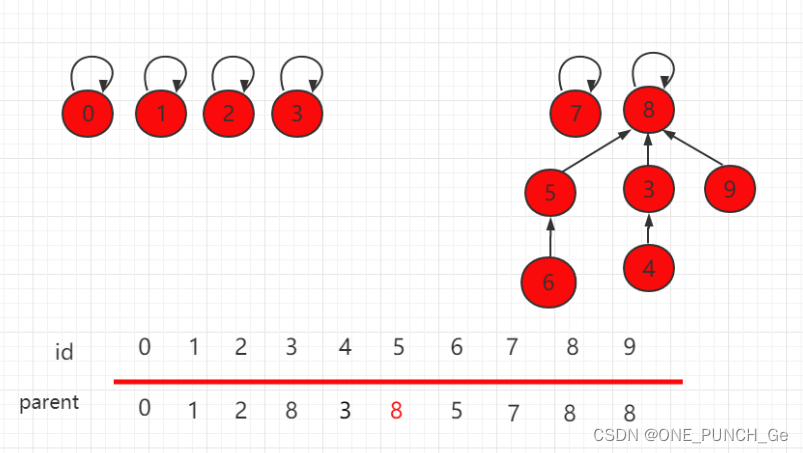
构建这种指向父节点的树形结构， 使用一个数组构建一棵指向父节点的树，parent[i] 表示 i 元素所指向的父节点。

...
private int[] parent;
private int count;  // 数据个数
...

查找过程, 查找元素 p 所对应的集合编号，不断去查询自己的父亲节点, 直到到达根节点，根节点的特点 parent[p] == p，O(h) 复杂度, h 为树的高度。

...
private int find(int p){
    assert( p >= 0 && p < count );
    while( p != parent[p] )
        p = parent[p];
    return p;
}
...

合并元素 p 和元素 q 所属的集合，分别查询两个元素的根节点，使其中一个根节点指向另外一个根节点，两个集合就合并了。这个操作是 O(h) 的时间复杂度，h 为树的高度。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    parent[pRoot] = qRoot;
}

Java 实例代码

UnionFind2.java 文件代码：

package runoob.union;
/**
 * 第二版unionFind
 */
public class UnionFind2 {
    // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    private int count;  // 数据个数
    // 构造函数
    public UnionFind2(int count){
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ )
            parent[i] = i;
    }
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
    }
}