LeetCode 428. Serialize and Deserialize N-ary Tree【树,BFS,DFS】困难

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

序列化是指将一个数据结构转化为位序列的过程，因此可以将其存储在文件中或内存缓冲区中，以便稍后在相同或不同的计算机环境中恢复结构。

设计一个序列化和反序列化 $N$ 叉树的算法。一个 $N$ 叉树是指每个节点都有不超过 $N$ 个孩子节点的有根树。序列化 / 反序列化算法的算法实现没有限制。你只需要保证 $N$ 叉树可以被序列化为一个字符串并且该字符串可以被反序列化成原树结构即可。

例如，你需要序列化下面的 3-叉 树。

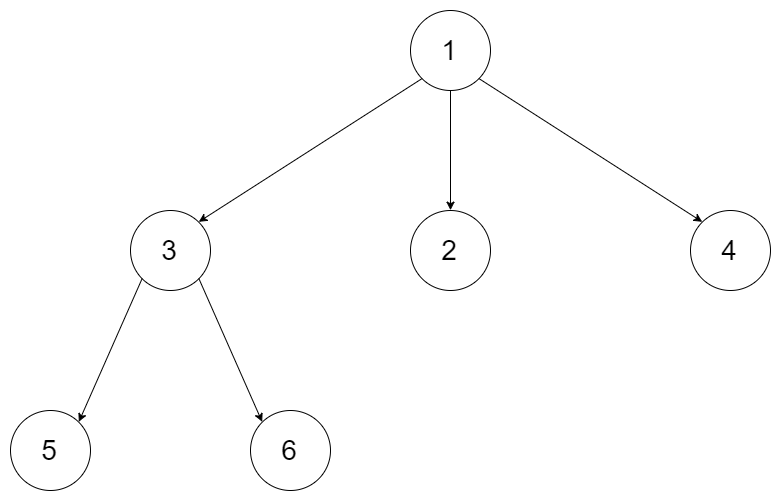
为 [1 [3[5 6] 2 4]]。你不需要以这种形式完成，你可以自己创造和实现不同的方法。

或者，您可以遵循 LeetCode 的层序遍历序列化格式，其中每组孩子节点由空值分隔。

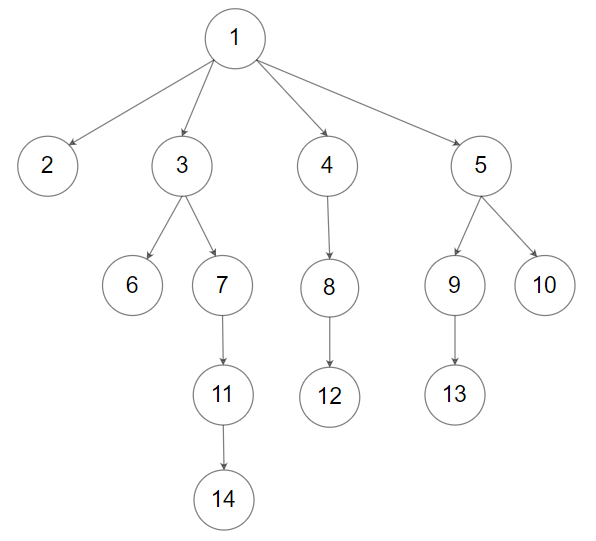
例如，上面的树可以序列化为 [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

你不一定要遵循以上建议的格式，有很多不同的格式，所以请发挥创造力，想出不同的方法来完成本题。

示例 1:

输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出: [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
1
2

示例 2:

输入: root = [1,null,3,2,4,null,5,6]
输出: [1,null,3,2,4,null,5,6]
1
2

示例 3:

输入: root = []
输出: []
1
2

提示：

• 树中节点数目的范围是 [0, 10^4].
• 0 <= Node.val <= 10^4
• $N$ 叉树的高度小于等于 1000
• 不要使用类成员 / 全局变量 / 静态变量来存储状态。你的序列化和反序列化算法应是无状态的。

---

类似题目：

• 449. 序列化和反序列化二叉搜索树
• 297. 二叉树的序列化与反序列化 困难
• 428. 序列化和反序列化 N 叉树 困难

---

解法 BFS+类似LeetCode层序遍历格式+StringJoiner

import java.util.StringJoiner;
class Codec {
    // Encodes a tree to a single string.
    public String serialize(Node root) {
        if (root == null) return "";
        StringJoiner sj = new StringJoiner(",");
        Deque<Node> queue = new ArrayDeque<>();
        queue.offer(root);
        sj.add(Integer.toString(root.val));
        sj.add(null);
        while (!queue.isEmpty()) {
            Node curr = queue.poll();
            for (Node node : curr.children) { // 将每个节点的子节点作为一组,由空值分隔
                sj.add(Integer.toString(node.val));
                queue.offer(node);
            }
            sj.add(null);
        }
        return sj.toString();
    }
	
    // Decodes your encoded data to tree.
    public Node deserialize(String data) {
        if (data.isEmpty()) return null;
        String[] tokens = data.split(",");
        Deque<Node> queue = new ArrayDeque<>();
        int index = 0;
        Node root = new Node(Integer.parseInt(tokens[index++]), new ArrayList<Node>());
        ++index; // 跳过null

        queue.offer(root); 
        while (!queue.isEmpty()) {
            Node curr = queue.poll();
            while (index < tokens.length) {
                if (tokens[index].equals("null")) {
                    ++index;
                    break;
                }
                Node node = new Node(Integer.parseInt(tokens[index++]), new ArrayList<Node>());
                curr.children.add(node);
                queue.offer(node);
            }
        }
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

当然，也可以选择类似JSON那样有层次的序列化格式。总之，序列化和反序列的题目很发散，各种解法都行。