代码随想录第33天 | ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯

509. 斐波那契数

//法一：
/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
  let bp=new Array(n)
  bp[0]=0
  bp[1]=1
  for(let i=2;i<=n;i++){
    bp[i]=bp[i-1]+bp[i-2]
  }
  return bp[n]
};

//法二，时间少，空间少，只需要维护两个数值就可以了，不需要记录整个序列。
/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    let sum = 0;
    let prev1 = 0;
    let prev2 = 1;
    for (let i = 1; i < n; i++) {
        sum = prev1 + prev2;
        prev1 = prev2;
        prev2 = sum;
    }
    return sum;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

70. 爬楼梯

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
  //2+bp(n-1)+bp(n-2)
    let bp=new Array(n+1)
    bp[1]=1
    bp[2]=2
  for(let i=3;i<=n;i++){
    bp[i]=bp[i-1]+bp[i-2]
  }
  return bp[n]
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

第一想法

2+bp(n-1)+bp(n-2)
比如有10步楼梯=1步+9步楼梯的方法+2步+8步楼梯的方法

746. 使用最小花费爬楼梯

/**
 * @param {number[]} cost
 * @return {number}
 */
var minCostClimbingStairs = function(cost) {
 let n=cost.length
  let dp=new Array(n)
//   dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。
  dp[0]=0
  dp[1]=0
  for(let i=2;i<=n;i++){
     dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
 }
 return dp[n]


 function min(a,b){
     return a>b?b:a
 }
};


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

想法

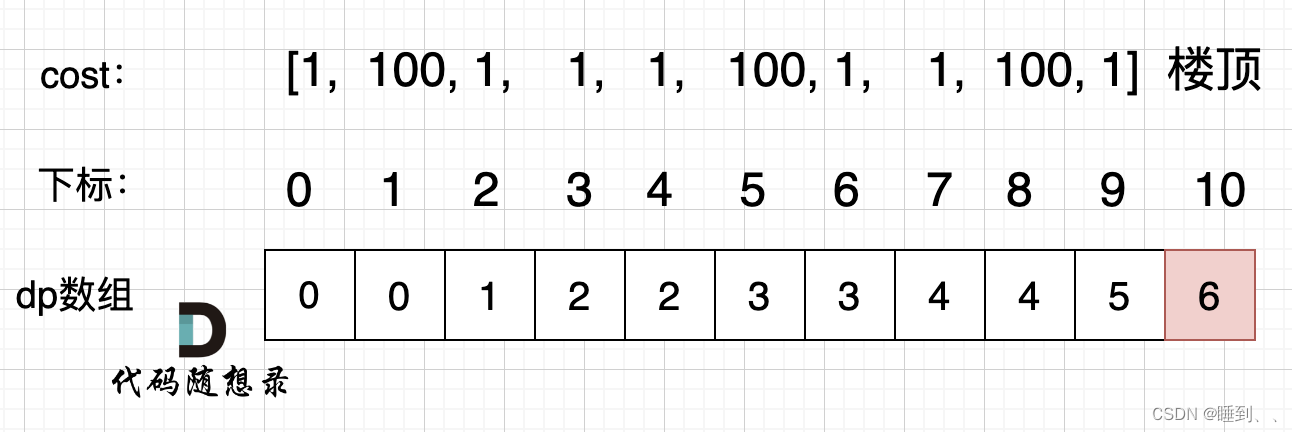
1. 确定dp数组以及下标的含义
   使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了。
   dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。
   对于dp数组的定义，大家一定要清晰！

2. 确定递推公式
   可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。
   dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
   dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
   那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？
   一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

3. dp数组如何初始化
   看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。
   那么 dp[0] 应该是多少呢？ 根据dp数组的定义，到达第0台阶所花费的最小体力为dp[0]，那么有同学可能想，那dp[0] 应该是 cost[0]，例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话，dp[0] 就是 cost[0] 应该是1。
   新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的，但从 第0 个台阶 往上跳的话，需要花费 cost[0]。
   所以初始化 dp[0] = 0，dp[1] = 0;
   
   

1

/**
 * @param {number[]} nums
 * @return {number[]}
 */


1
2
3
4
5
6

第一想法

困难

收获