【C++】递归，搜索与回溯算法入门介绍和专题一讲解

个人主页：🍝在肯德基吃麻辣烫
我的gitee：C++仓库
个人专栏：C++专栏

前言

从本文开始进入递归，搜索与回溯算法专题讲解。

---

---

一、名词解释

1、什么是递归？

递归就是函数自己调用自己。

---

2、为什么会用到递归？

递归的本质是：

主问题：—>相同的子问题
子问题：—>相同的子问题

3、如何理解递归？

通过：

• 1）通过递归的细节展开图（前期可以，过了前期一定不能再用了）
• 2）通过二叉树中的题目
• 3）宏观看待递归问题（重要）

越往后学越发现，如果只抓住递归的细节展开图，你会发现你根本就学不好递归这个东西，递归的细节展开图只是为了辅助你读过新手期，如果你后面还在用它，那么你往往是学不好递归的。

那么：如何理解宏观看待递归问题这个点呢？

可以分为几个部分：

• • 1）不要再在意递归的细节展开图
• • 2）把递归的函数当成一个黑盒子
• • 3）相信这个黑盒子一定能完成这个任务

---

4、如何写好递归？

写好一个递归也分为三点：

• 1）先找到相同的子问题（函数头的设计）
• 2）只关心某一个子问题是如何解决的（函数体的书写）
• 3）递归出口

二、搜索vs深度优先遍历vs深度优先搜索vs宽度优先遍历vs宽度优先搜索vs暴搜

1、深度优先遍历vs深度优先搜索

其实，一句话就能概括下来：
遍历是形式，搜索是目的。

所以，我们平时说的深度优先遍历和深度优先搜索，其实他们俩是一样的。
都可以叫做dfs。

2、宽度优先遍历vs宽度优先搜索

其实，一句话就能概括下来：
遍历是形式，搜索是目的。

所以，我们平时说的宽度优先遍历和宽度优先搜索，其实他们俩是一样的。
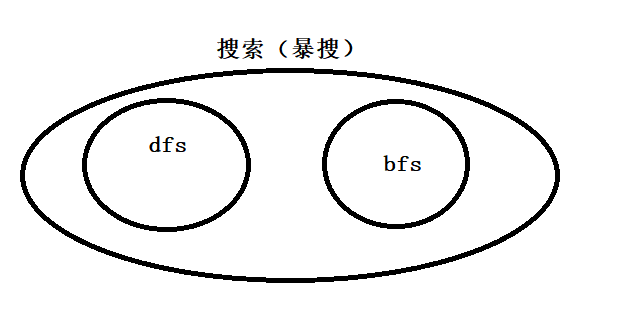
都可以叫做bfs。

3、关系图

我们所说的搜索，其实就是暴搜。

4. 搜索问题的拓展

我们刚开始学习搜索时，总以为dfs和bfs这两个搜索都只与二叉树有关。其实不然。
从下面的例题开始你会发现，很多东西都能使用dfs进行求解。

三、回溯与剪枝

这两个名词听起来貌似很高大上，其实用一个例子就能解释清楚了。

下面来看一个迷宫问题：

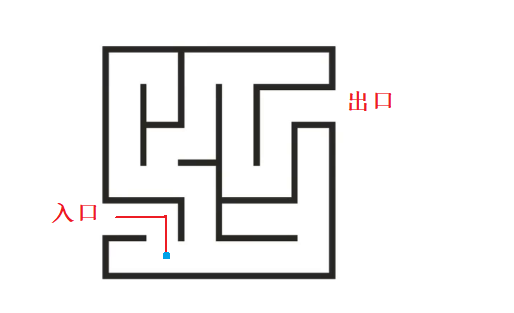
入口和出口如上：我们从入口出发，往右边走遇到墙壁之后，往下走。走到蓝色标记，也就是拐角点的地方后，这就是一个岔路口，此时我们有两种选择：

• 1）往左边走
• 2）往右边走

当我们选择往左边走时，如下图：

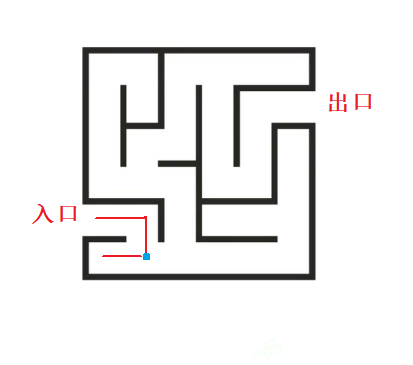
会遇到墙壁，此时我们就需要原路返回。

这个从某一位置出发，一条道走到黑，再沿着原路返回的过程，就叫做回溯。

回溯的这条路径，我们用绿色来标记。

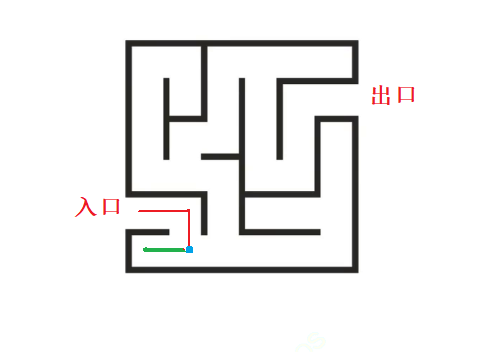
此时又走到了蓝色拐点，在这个岔路口我们有三种选择：
1）往上走
2）往左走
3）往右走

可是，我们最初是从上面下来的，然后沿着左边走，走不通之后再返回来的。
所以，我们只有一个选择：往右走。

而这个判断的过程，也就是选择路径的过程，就叫做剪枝。

将往上走的路径剪掉，将往左走的路径剪掉，就是剪枝。

四、专题一

1. 汉诺塔问题

点我直达

算法分析

1.找到相同的子问题：

---

当n = 1时：

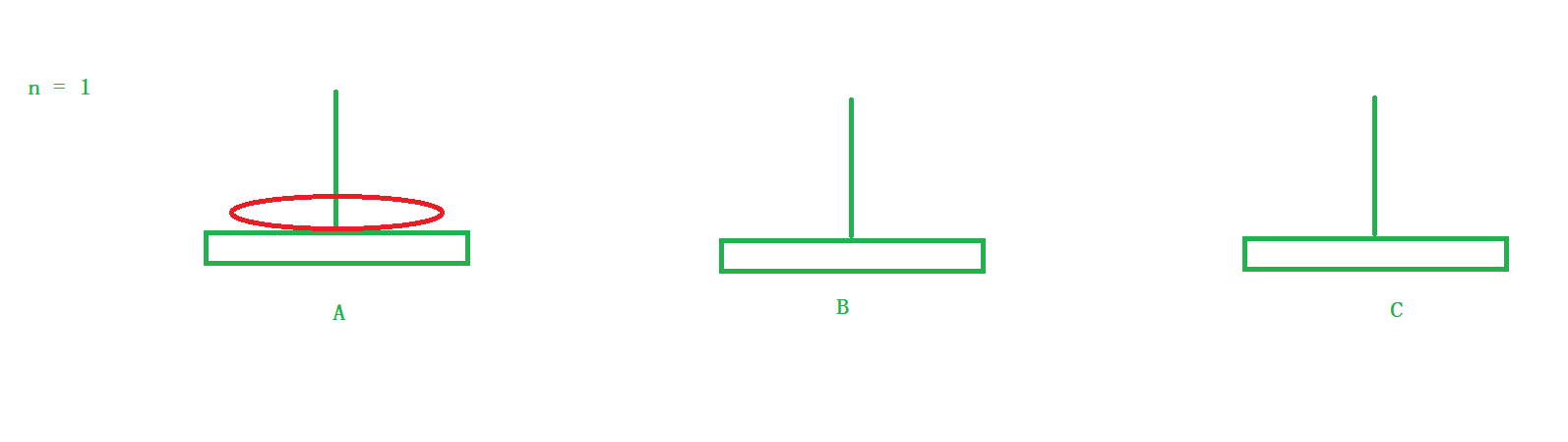
直接将盘子从A柱子挪到C柱子即可。

---

当n = 2 时

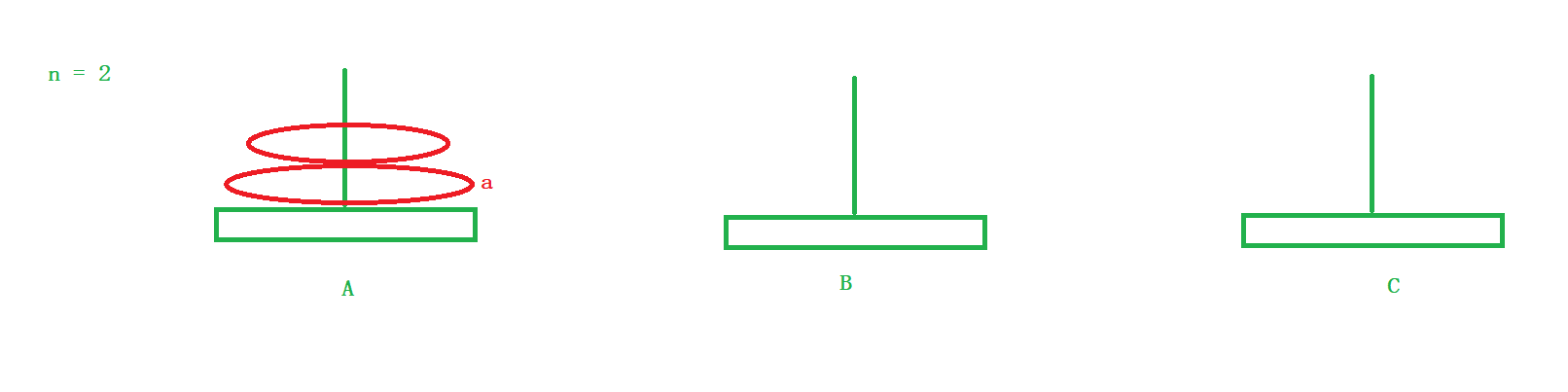
分为三步走：

1）我们需要将盘子a上面的盘子借助C柱子移动到B柱子。

2）将a盘子移动到C柱子上

3）将B柱子上的所有盘子借助A盘子移动到C柱子上。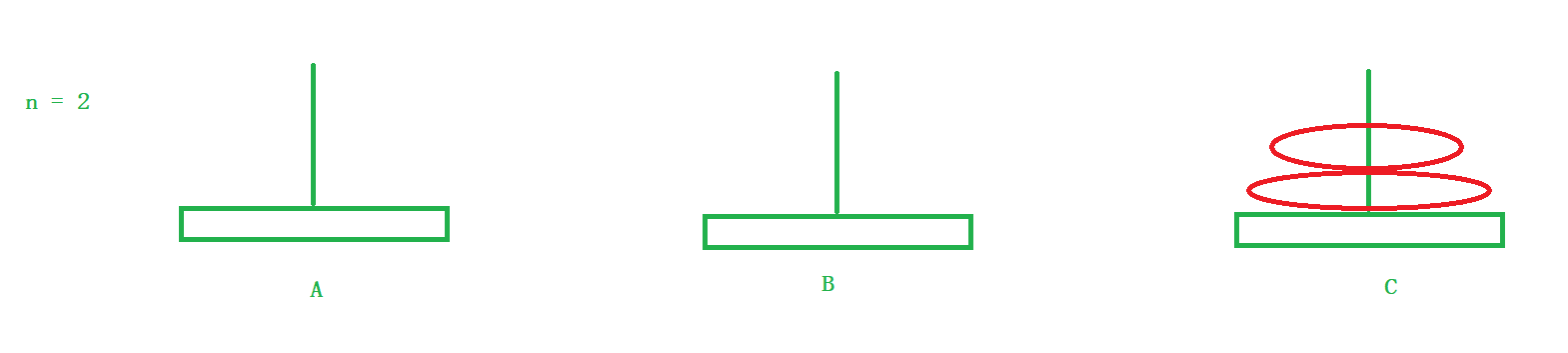

---

当n = 3 时

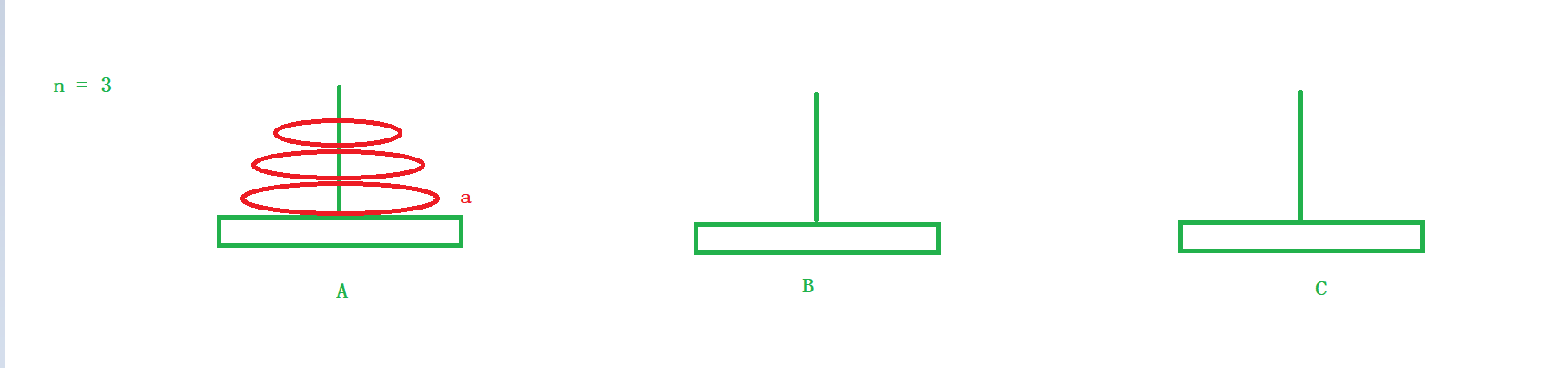
与第二步相同：
分为三步走
1）将a盘子上面的所有盘子借助C柱子移动到B柱子上。

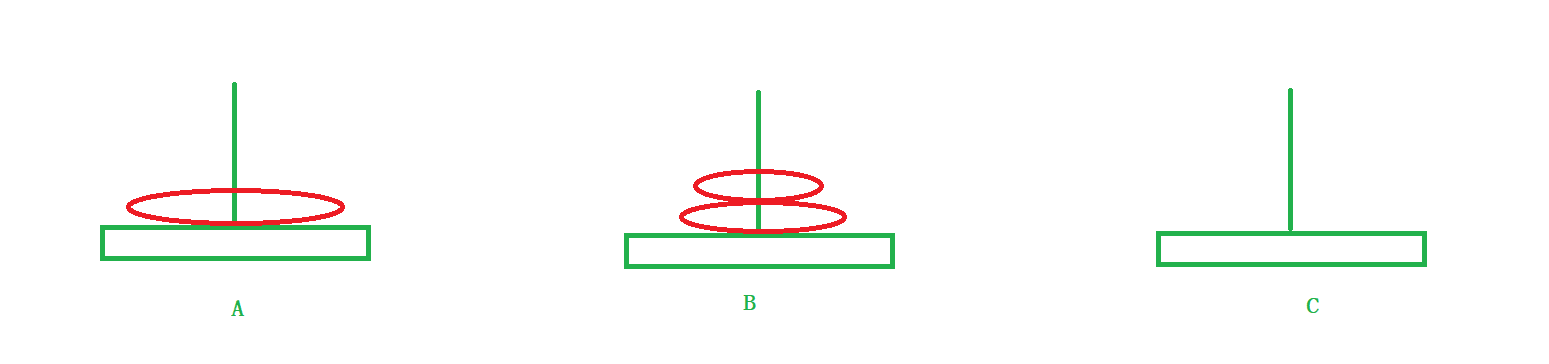
2）将a盘子移动到C柱子上。

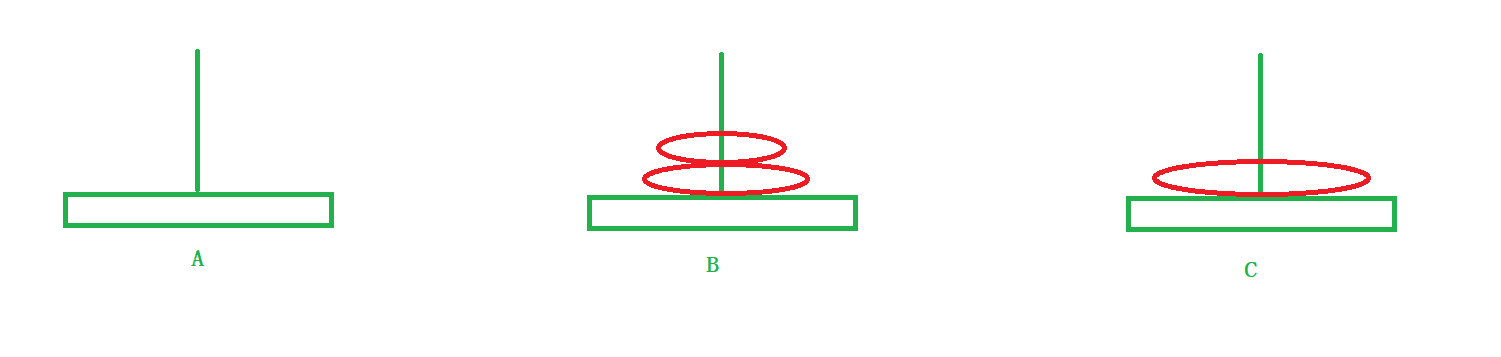
3）将B柱子上面的所有盘子借助A柱子移动到C柱子上。

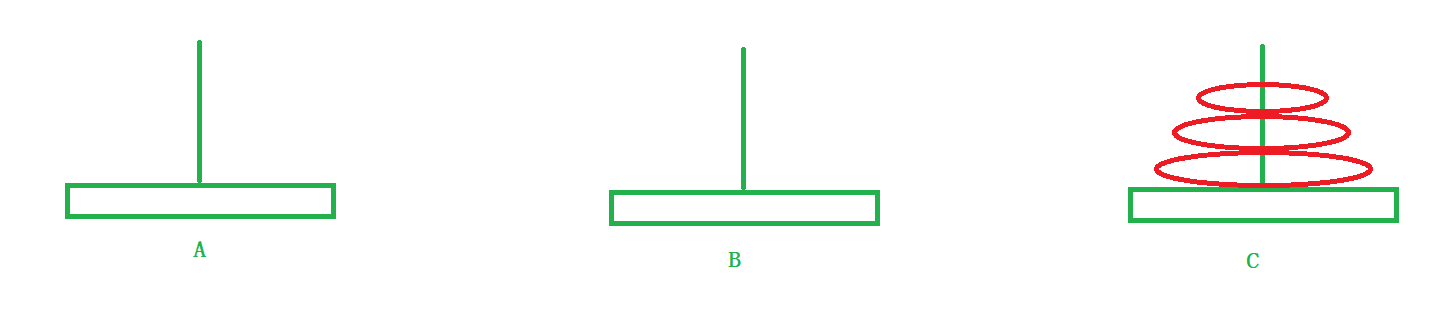
2.只关心某一个子问题如何解决。

所以我们会发现，当n >= 2时，都会执行相同的子问题的操作。操作如下：

• 1）将a盘子上面的所有盘子通过C柱子挪到B柱子上。
• 2）将a盘子挪到C盘子上。
• 3）将B柱子上面的所有盘子挪到C柱子上。

---

在这整个过程中，你要相信一件事情：
你交给dfs这个函数的任务是：

我要把所有盘子全部借助一个柱子挪到另一个柱子上。

并且要相信dfs这个函数一定能完成这个任务。

这就是宏观看待问题的思路。

3.递归出口
递归出口就是当n = 1时，你会发现跟当n = 其他数的操作步骤是不一样的。
当n = 1时，直接将a盘子移动到C柱子即可。

代码编写

class Solution {
public:
//1.重复的子问题（函数头）
//要将A柱子上面的所有盘子借助B柱子全部转移到C柱子上面

//2.只关心某一个子问题在做什么（函数体）

//3.递归出口

    void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n) 
    {
        if(n == 1)
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }

        dfs(A,C,B,n-1);
        C.push_back(A.back());
        A.pop_back();
        dfs(B,A,C,n-1);
    }
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) 
    {
        int n = A.size();
        dfs(A,B,C,n);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

总结

提示：这里对文章进行总结：

本文章详细讲解了递归，搜索与回溯算法的入门理解级操作，以及通过一道例题感受一下dfs这种算法的强大之处，关键在于dfs写起来特别简单。

学好dfs，是进入大厂的必备技能。