• 有向图和无向图的表示方式(邻接矩阵，邻接表)

    目录

    一.邻接矩阵

    1.无向图​编辑

    2.有向图

    补充：网（有权图）的邻接矩阵表示法

    二.邻接表

    1.无向图

    2.有向图

    三.邻接矩阵与邻接表的关系

    一.邻接矩阵

    1.无向图

    （1）对角线上是每一个顶点与自身之间的关系，没有到自身的边，所以对角线上为0

    （2）无向图的邻接矩阵是对称的

    两个顶点之间如果有边的话，那么两个顶点互为邻接关系，值为1

    （3）顶点i的度=第i行（列）中1的个数

    注：完全图的邻接矩阵，对角元素为0，其余为1

    2.有向图

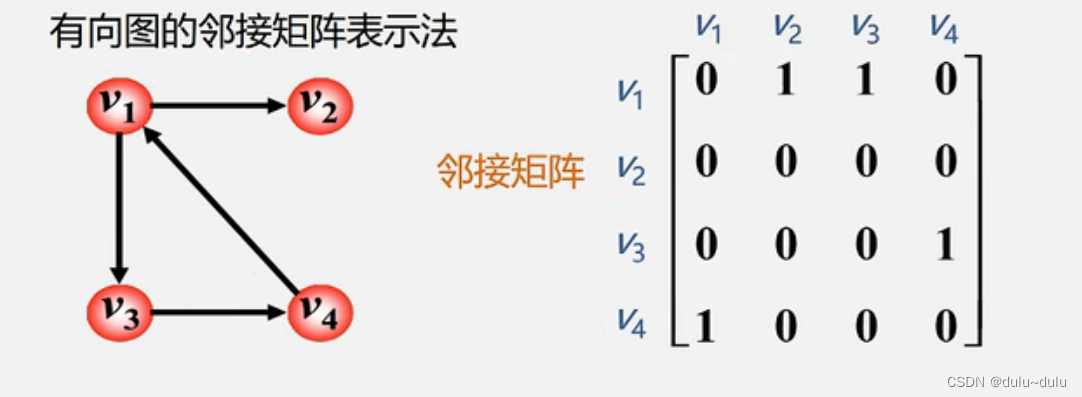
    （1）在有向图的邻接矩阵中

    第i行含义：以结点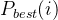v_{i}为尾的弧（即出度边）

    顶点的出度=第i行元素之和

    第i列含义：以结点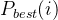v_{i}为头的弧（即入度边）

    顶点的入度=第i列元素之和

    顶点的度=第i行元素之和+第i列元素之和

    （2）有向图的邻接矩阵可能是不对称的

    补充：网（有权图）的邻接矩阵表示法

    邻接矩阵存储

    1. #define MaxInt 32767
    2. #define MVNum 100    //最大顶点数
    3. typedef char VerTexType;    //设顶点的数据类型为字符型
    4. typedef int ArcType;    //假设边的权值类型为整型
    5.  
    6. typedef struct{
    7.     VerTex vex[MVNum];    //顶点表
    8.     ArcType arcs[MVNum][MVNum];    //邻接矩阵
    9.     int vexnum,arcnum;    //图的当前点数和边数
    10. }AMGraph;
    11.

     以无向网为例

    1. int LocateVex(AMGraph G,VertexType u)
    2. {
    3. //查找图G中的顶点u,存在则返回顶点表中的下标;否则返回-1
    4.     int i;
    5.     for(i=0;i<G.vexnum;++i)//有几条边就循环多少次
    6.     {
    7.         if(u==G.vexs[i])
    8.             return i;
    9.         return -1;
    10.     }
    11. }
    12.  
    13. Status CreateUDN(AMGraph &G)
    14. {
    15.    int i;
    16.    cin>>G.vexnum>>G.arcnum;//总顶点,总边数
    17.     for(i=0;i<G.vexnum;++i)
    18.         cin>>G.vexs[i];//依次输入点的信息
    19.     for(i=0;i<G.vexnum;++i)//初始化邻接矩阵
    20.     {
    21.         for(int j=0;j<G.vexnum;++j)
    22.         {
    23.             G.arcs[i][j]=MaxInt;//边的权值均置为极大值
    24.         }
    25.     }
    26.     for(int k=0;k<G.arcnum;++k)//构造邻接矩阵
    27.     {
    28.         cin>>v1>>v2>>w;//输入一条边所依附的顶点以及边的权值
    29.         i=LocateVex(G,v1);
    30.         j=LocateVex(G,v2);//确定v1,v2在G中的位置
    31.         G.arcs[i][j]=w;//边<v1,v2>的权值置w
    32.         G.arcs[j][i]=G.arcs[i][j];//<v1,v2>的对称边<v2,v1>的权值也为w
    33.     }
    34.     return OK;
    35. }

    无向图，有向网,有向图与无向网是类似的

    •对于无向图而言，其与无向网相比没有权值

    初始化邻接矩阵时，w=0 ，构建邻接矩阵时，w=1

    1. Status CreateUDG(AMGraph &G)
    2. {
    3.    int i;
    4.    cin>>G.vexnum>>G.arcnum;//总顶点,总边数
    5.     for(i=0;i<G.vexnum;++i)
    6.         cin>>G.vexs[i];//依次输入点的信息
    7.     for(i=0;i<G.vexnum;++i)//初始化邻接矩阵
    8.     {
    9.         for(int j=0;j<G.vexnum;++j)
    10.         {
    11.             G.arcs[i][j]=0;//边的权值均置为0
    12.         }
    13.     }
    14.     for(int k=0;k<G.arcnum;++k)//构造邻接矩阵
    15.     {
    16.         cin>>v1>>v2;//输入一条边所依附的顶点
    17.         int w=1;//1表示连接、0表示无连接
    18.         i=LocateVex(G,v1);
    19.         j=LocateVex(G,v2);//确定v1,v2在G中的位置
    20.         G.arcs[i][j]=w;//边<v1,v2>的权值置w
    21.         G.arcs[j][i]=G.arcs[i][j];//<v1,v2>的对称边<v2,v1>的权值也为w
    22.     }
    23.     return OK;
    24. }

    •对于有向网而言，与无向网不同的是，其每一条弧，都是从一个顶点指向另外一个顶点的

    仅为G.arcs[i][j]赋值，不为G.arcs[j][i]赋值

    1. Status CreateDN(AMGraph &G)
    2. {
    3.    int i;
    4.    cin>>G.vexnum>>G.arcnum;//总顶点,总边数
    5.     for(i=0;i<G.vexnum;++i)
    6.         cin>>G.vexs[i];//依次输入点的信息
    7.     for(i=0;i<G.vexnum;++i)//初始化邻接矩阵
    8.     {
    9.         for(int j=0;j<G.vexnum;++j)
    10.         {
    11.             G.arcs[i][j]=MaxInt;//边的权值均置为极大值
    12.         }
    13.     }
    14.     for(int k=0;k<G.arcnum;++k)//构造邻接矩阵
    15.     {
    16.         cin>>v1>>v2>>w;//输入一条边所依附的顶点以及边的权值
    17.         i=LocateVex(G,v1);
    18.         j=LocateVex(G,v2);//确定v1,v2在G中的位置
    19.         G.arcs[i][j]=w;//边<v1,v2>的权值置w
    20.     }
    21.     return OK;
    22. }

    •对于有向图而言，只需要将无向图和有向网的修改结合一下就行

    没有权值，连接两个顶点的边是弧 

    1. Status CreateDG(AMGraph &G)
    2. {
    3.    int i;
    4.    cin>>G.vexnum>>G.arcnum;//总顶点,总边数
    5.     for(i=0;i<G.vexnum;++i)
    6.         cin>>G.vexs[i];//依次输入点的信息
    7.     for(i=0;i<G.vexnum;++i)//初始化邻接矩阵
    8.     {
    9.         for(int j=0;j<G.vexnum;++j)
    10.         {
    11.             G.arcs[i][j]=0;//边的权值均置为0
    12.         }
    13.     }
    14.     for(int k=0;k<G.arcnum;++k)//构造邻接矩阵
    15.     {
    16.         cin>>v1>>v2;//输入一条边所依附的顶点
    17.         int w=1;//1表示连接、0表示无连接
    18.         i=LocateVex(G,v1);
    19.         j=LocateVex(G,v2);//确定v1,v2在G中的位置
    20.         G.arcs[i][j]=w;//边<v1,v2>的权值置w
    21.     }
    22.     return OK;
    23. }

    邻接矩阵的优点

     

    •方便检查任意一对顶点间是否存在边

    •方便找任一顶点的所有“邻接点”（有边直接相连的顶点）

    •方便计算任一顶点的“度”(从该点发出的边数为“出度”，指向该点的边数为“入度”)

            •无向图:对应行 (或列)非0元素的个数

            •有向图:对应行非0元素的个数是“出度”;对应列非0元素的个数是“入度

    邻接矩阵的缺点

    •不便于增加和删除顶点

    •邻接矩阵的空间复杂度为O(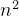n^{2}),跟其有的边的条数无关，只与其顶点数有关，无论边少还是边多，空间复杂度都为O(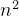n^{2})，浪费空间----存稀疏图（点很多而边很少）有大量无效元素

    •浪费时间----统计稀疏图中一共有多少条边，因为必须遍历所有元素

    二.邻接表

    1.无向图

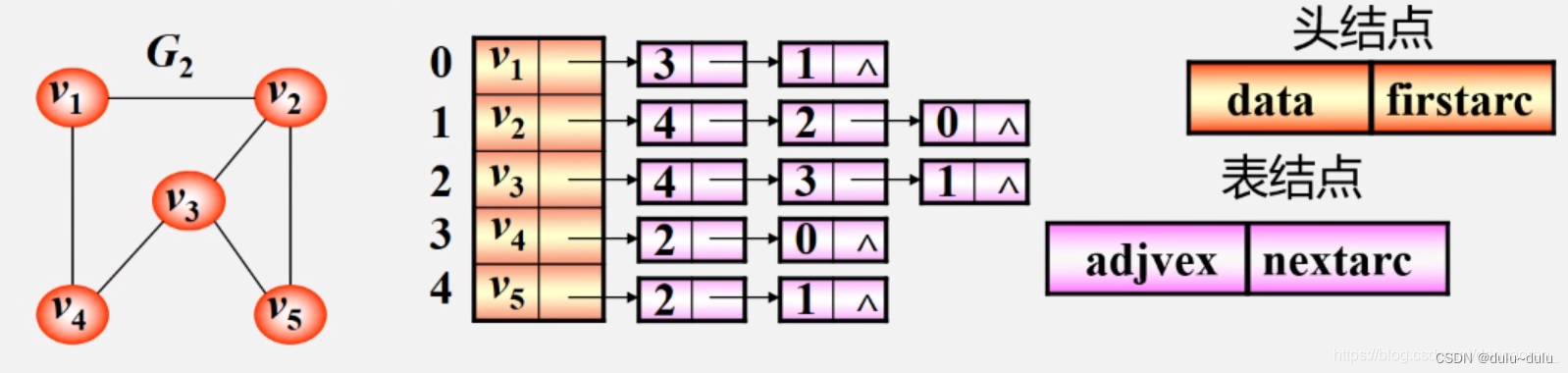
    顶点：按编号顺序存储在一维数组中

    这里的一维数组和邻接矩阵中的一维数组不同，数组中每个元素有两个成员

    第一个是数据元素的信息，第二个是指针，存储的是第一个边的地址

    关联同一顶点的边：用线性链表存储,例如3，表示邻接的顶点是下标为3的元素（v4）

    如果有边\弧的信息，还可以在表结点中增加一项

    第一个表示邻接点在顶点表中的序号

    第二个元素是一个指针，指向的是下一条边（弧）

    第三个元素表示边的信息（权值）

    （1）邻接表是不唯一

    例如“v1”指针指向的是邻接点v4和v2的下标，分别为3，1，这些边的顺序是可以改变的。

    （2）若无向图中有n个顶点，e条边，则其邻接表需n个头结点和2e个表结点，适宜存储稀疏图。

    使用每条边时会出现两次，从v1到v2和从v2到v1用的是同一条边，所以有e条边，就有2e个表结点

    所以无向图的存储空间为O(n+2e):n表示点，2e表示边

    有向图的存储空间为O(n+e)

    注对于邻接矩阵而言，存储空间为O(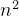n^{2}),所以邻接表在存储稀疏图时比较节省空间

     （3）无向图中顶点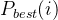v_{i}的度为第i个单链表中的结点数

    •顶点的存储结构

    1. typedef struct VNode
    2. {
    3. 	VerTexType data;         //顶点信息
    4. 	ArcNode *firstarc;       //指向第一条依附该顶点的边的指针
    5. }VNode,AdjList[MVNum];
    6. 注:AdjList[MVNum]==VNnode v[MVNum]

    •弧(边)的结点结构

    1. #define MVNum 100                //最大顶点数
    2. typedef struct ArcNode           //边结点
    3. {
    4. 	int adjvex;                  //该边所指向的顶点的位置
    5. 	struct ArcNode *nextarc;     //指向下一条边的指针
    6. 	OtherInfo info;              //和边相关的信息(权值等)
    7. }ArcNode;

    •图的结构定义

    1. typedef struct
    2. {
    3. 	AdjList vertices;      //存放各个顶点的数组
    4. 	int vexnum, arcnum;    //图的当前顶点数和弧数
    5. }ALGraph;

    •邻接表操作举例说明

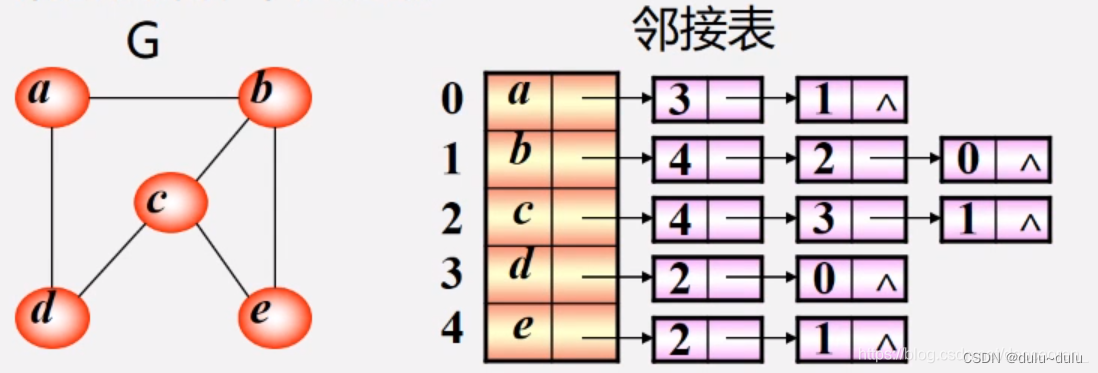
    1. ALGraph G;                    //定义了邻接表表示的图G
    2. G.vexnum = 5; G.arcnum = 6;   //图G中包含5个顶点，6条边
    3. G.vertices[1].data = 'b';     //图G中的第2个顶点是b
    4. p = G.vertices[1].firstarc;   //指针p指向顶点b的第一条边结点
    5. p->adjvex = 4;                //指针p所指边结点是到下标为4的结点的边
    2.有向图

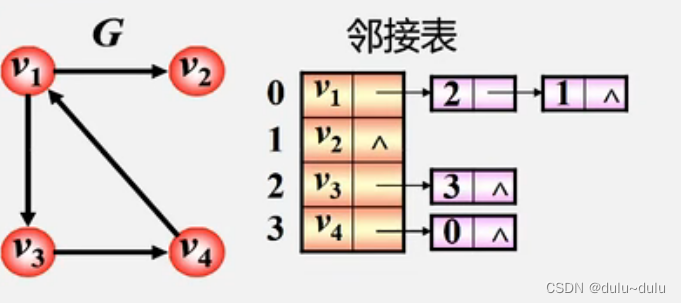
    （1）顶点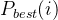v_{i}的出度为第i个单链表中的结点个数

    （2）顶点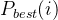v_{i}的入度为整个单链表中邻接点域值是（i-1）的结点个数

    根据以上结论，可以看出对于这样的每一个顶点存储出度边的有向图而言，找出度是容易的，找入度则比较难，例如，找终点为v1的边，那么就需要遍历所有边结点，找到邻结点为0的入度边

     也可以每一个顶点存储其入度边，如下图：逆邻接表

    和邻接表的结论相反：找入度容易，找出度难

    （1）顶点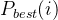v_{i}的入度为第i个单链表中的结点个数

    （2）顶点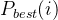v_{i}的出度为整个单链表中邻接点域值是（i-1）的结点个数

    例题：画出该邻接表对应的网络图

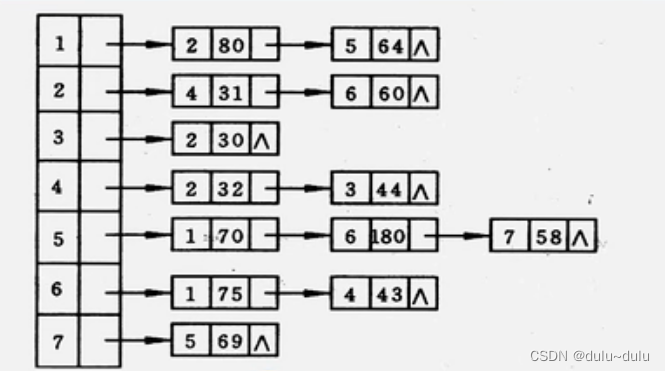
    结果如下


     

    用邻接表创建无向图

    1. int LocateVex(AMGraph G,VertexType u)
    2. {
    3. //查找图G中的顶点u,存在则返回顶点表中的下标;否则返回-1
    4.     int i;
    5.     for(i=0;i<G.vexnum;++i)//有几条边就循环多少次
    6.     {
    7.         if(u==G.vexs[i])
    8.             return i;
    9.         return -1;
    10.     }
    11. }
    12.  
    13. Status CreateUDG(ALGraph &G)
    14. {
    15.     int i, j, k;
    16.     cin >> G.vexnum >> G.arcnum;                            // 输入总顶点数，总边数
    17.     for (i = 0; i < G.vexnum; ++i)                          // 输入各点，构造表头(顶点)节点表
    18.     {
    19.         cin >> G.vertices[i].data;                          // 输入顶点值
    20.         G.vertices[i].firstarc = NULL;                      // 初始化表头结点的指针域
    21.     }
    22.     for (k = 0; k < G.arcnum; ++k)                          // 输入各边，构造邻接表
    23.     {
    24.         int v1, v2;
    25.         cin >> v1 >> v2;                                    // 输入一条边依附的两个顶点
    26.         i = LocateVex(G, v1);
    27.         j = LocateVex(G, v2);
    28.         ArcNode* p1 = new ArcNode;                           // 生成一个新的边结点*p1
    29.         p1->adjvex = j;                                     // 邻接点序号为j
    30.         p1->nextarc = G.vertices[i].firstarc;
    31.         G.vertices[i].firstarc = p1;                         // 将新结点*p1插入顶点vi的边表头部(头插法)
    32.         ArcNode* p2 = new ArcNode;                           // 生成一个新的边结点*p2
    33.         p2->adjvex = i;                                     // 邻接点序号为i
    34.         p2->nextarc = G.vertices[j].firstarc;
    35.         G.vertices[j].firstarc = p2;                         // 将新结点*p2插入顶点vj的边表头部(头插法)
    36.     }
    37.     return OK;
    38. }

    这里的头插法特别解释一下

    p1->nextarc = G.vertices[i].firstarc;  
    G.vertices[i].firstarc = p1;           //将新结点*p1插入顶点vi的边表头部(头插法)

    用邻接表创建有向图

    只需将边改为弧，将以下代码去掉

            p2 = new ArcNode;                      //生成一个新的边结点*p2
            p2->adjvex = i;                        //邻接点序号为i
            p2->nextarc = G.vertices[j].firstarc;
            G.vertices[j].firstarc = p2;           //将新结点*p2插入顶点vj的边表头部(头插法)

    1. Status CreateDG(ALGraph &G)
    2. {
    3.     cin >> G.vexnum >> G.arcnum;                        // 输入总顶点数，总边数
    4.     for (int i = 0; i < G.vexnum; ++i)                   // 输入各点，构造表头(顶点)节点表
    5.     {
    6.         cin >> G.vertices[i].data;                      // 输入顶点值
    7.         G.vertices[i].firstarc = NULL;                  // 初始化表头结点的指针域
    8.     }
    9.     for (int k = 0; k < G.arcnum; ++k)                   // 输入各边，构造邻接表
    10.     {
    11.         int v1, v2;
    12.         cin >> v1 >> v2;                                 // 输入一条边依附的两个顶点
    13.         int i = LocateVex(G, v1);
    14.         int j = LocateVex(G, v2);
    15.         ArcNode* p = new ArcNode;                         // 生成一个新的边结点*p
    16.         p->adjvex = j;                                   // 邻接点序号为j
    17.         p->nextarc = G.vertices[i].firstarc;             
    18.         G.vertices[i].firstarc = p;                      // 将新结点*p插入顶点vi的边表头部(头插法)
    19.     }
    20.     return OK;
    21. }

     用邻接表创建有向网

    只需加入weight（权重值即可）

    cin >> v1 >> v2 >> weight;

    p->info=weight;

    1. Status CreateWeightedDN(ALGraph &G)
    2. {
    3.     cin >> G.vexnum >> G.arcnum;                        // 输入总顶点数，总边数
    4.     for (int i = 0; i < G.vexnum; ++i)                   // 输入各点，构造表头(顶点)节点表
    5.     {
    6.         cin >> G.vertices[i].data;                      // 输入顶点值
    7.         G.vertices[i].firstarc = NULL;                  // 初始化表头结点的指针域
    8.     }
    9.     for (int k = 0; k < G.arcnum; ++k)                   // 输入各边，构造邻接表
    10.     {
    11.         int v1, v2, weight;
    12.         cin >> v1 >> v2 >> weight;                       // 输入一条边依附的两个顶点和权值
    13.         int i = LocateVex(G, v1);
    14.         int j = LocateVex(G, v2);
    15.         ArcNode* p = new ArcNode;                         // 生成一个新的边结点*p
    16.         p->adjvex = j;                                   // 邻接点序号为j
    17.         p->info = weight;                              // 边的权值为weight
    18.         p->nextarc = G.vertices[i].firstarc;             
    19.         G.vertices[i].firstarc = p;                      // 将新结点*p插入顶点vi的边表头部(头插法)
    20.     }
    21.     return OK;
    22. }

     用邻接表创建无向网

    只需在无向图的基础上加入weight（权重值即可）

    cin >> v1 >> v2 >> weight;

    p1->info=weight;

    p2->info=weight;

    1. Status CreateWeightedUDN(ALGraph &G)
    2. {
    3.     cin >> G.vexnum >> G.arcnum;                            // 输入总顶点数，总边数
    4.     for (int i = 0; i < G.vexnum; ++i)                       // 输入各点，构造表头(顶点)节点表
    5.     {
    6.         cin >> G.vertices[i].data;                          // 输入顶点值
    7.         G.vertices[i].firstarc = NULL;                      // 初始化表头结点的指针域
    8.     }
    9.     for (int k = 0; k < G.arcnum; ++k)                       // 输入各边，构造邻接表
    10.     {
    11.         int v1, v2, weight;
    12.         cin >> v1 >> v2 >> weight;                           // 输入一条边依附的两个顶点和权值
    13.         int i = LocateVex(G, v1);
    14.         int j = LocateVex(G, v2);
    15.         ArcNode* p1 = new ArcNode;                            // 生成一个新的边结点*p1
    16.         p1->adjvex = j;                                      // 邻接点序号为j
    17.         p1->info = weight;                                 // 边的权值为weight
    18.         p1->nextarc = G.vertices[i].firstarc;
    19.         G.vertices[i].firstarc = p1;                         // 将新结点*p1插入顶点vi的边表头部(头插法)
    20.         ArcNode* p2 = new ArcNode;                            // 生成一个新的边结点*p2
    21.         p2->adjvex = i;                                      // 邻接点序号为i
    22.         p2->info = weight;                                 // 边的权值为weight
    23.         p2->nextarc = G.vertices[j].firstarc;
    24.         G.vertices[j].firstarc = p2;                         // 将新结点*p2插入顶点vj的边表头部(头插法)
    25.     }
    26.     return OK;
    27. }

     邻接表的特点

    •方便找任一顶点的所有“邻接点”
    •节约稀疏图的空间
            •需要N个头指针 + 2E个结点 (每个结点至少2个域)

    •方便计算任一顶点的“度”
    对无向图:是的
    对有向图:只能计算“出度”需要构造"逆邻接表"(存指向自己的边)来方便计算"入度"

    •不方便检查任意一对顶点间是否存在边

    三.邻接矩阵与邻接表的关系

    1.联系:邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数

    2.区别:
    ①对于任一确定的无向图，邻接矩阵是唯一的 (行列号与顶点编号致)，但邻接表不唯一 (链接次序与顶点编号无关，与链接的算法有关（头插法或尾插法）)

    ②邻接矩阵的空间复杂度为O(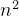n^{2}）,而邻接表的空间复杂度为O(n+e),对于稀疏图而言，用邻接表的方式存储，空间复杂度更低。

    3.用途：邻接矩阵多用于稠密图，邻接表多用于稀疏图。

  • 相关阅读:
    谷歌云计算技术基础架构,谷歌卷积神经网络
    win11下配置ftp
    vue项目 H5 动态设置浏览器标题
    【Hadoop】HDFS 原理
    [前端进阶] 工程/工具篇
    Linux NVMe Driver学习笔记之6：Admin Queue与Blk-mq初始化
    java 企业工程管理系统软件源码+Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
    在Android开发中如何使用OpenSL ES库播放解码后的pcm音频文件？
    Ribbon 负载均衡原理和策略
    「避坑宝典」为大家分享笔者在22 年所遇到“匪夷所思”的 Bug 趣事
  • 原文地址：https://blog.csdn.net/weixin_69884785/article/details/132629111