• [LeetCode]栈,队列相关题目(C语言实现)

    文章目录

    LeetCode20. 有效的括号

    题目

    给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

    要求

    有效字符串需满足：

    左括号必须用相同类型的右括号闭合。
    左括号必须以正确的顺序闭合。
    每个右括号都有一个对应的相同类型的左括号。

    思路
    用栈实现

    1. 如果是左括号, 直接将左括号入栈
    2. 如果是右括号, 如果此时栈为空, 返回 false; 将栈顶元素弹出栈, 如果栈顶元素不是对应的左括号, 返回 false; 如果栈顶元素是对应左括号, 出栈
    3. 遍历完字符串, 判断此时栈是否为空. 为空返回 true; 不为空返回 false

    代码实现

    #define N 10000
bool isValid(char * s)
{
    char stack[N] = {0,};   //创建栈数组
    int top = 0;            //top指向栈顶元素的后一个空间
    char topVal = 0;        //用来存放栈顶元素

    while (*s)
    {
        //如果是左括号
        if (*s == '{' || *s == '(' || *s == '[')
        {
            //入栈
            stack[top] = *s;
            top++;
        }
        //如果是右括号
        else
        {
            //如果此时栈为空, 直接返回false
            if (top == 0)
            {
                return false;
            }

            topVal = stack[top - 1];    //得到栈顶元素
            top--;  //栈顶元素出栈

            //如果右括号不是其对应的左括号, 直接返回false
            if ((*s == ']' && topVal != '[')
            || (*s == ')' && topVal != '(')
            || (*s == '}' && topVal != '{'))
            {
                return false;
            }
        }
        s++;
    }

    //如果遍历完字符串, 栈仍为空, 则返回true
    if (top == 0)
        return true;
    else
        return false;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45

    LeetCode225. 用队列实现栈

    题目

    请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

    OJ链接

    要求

    实现 MyStack 类：

    void push(int x) 将元素 x 压入栈顶。
    int pop() 移除并返回栈顶元素。
    int top() 返回栈顶元素。
    boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

    思路

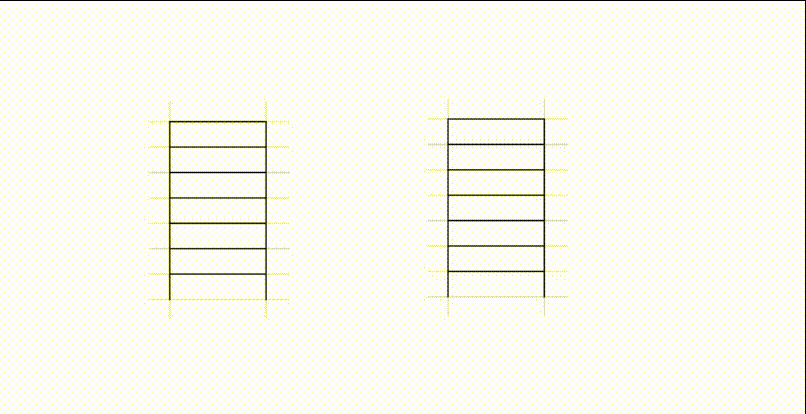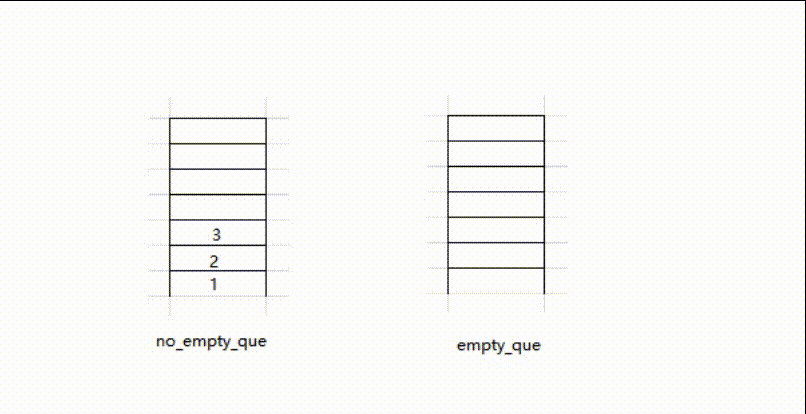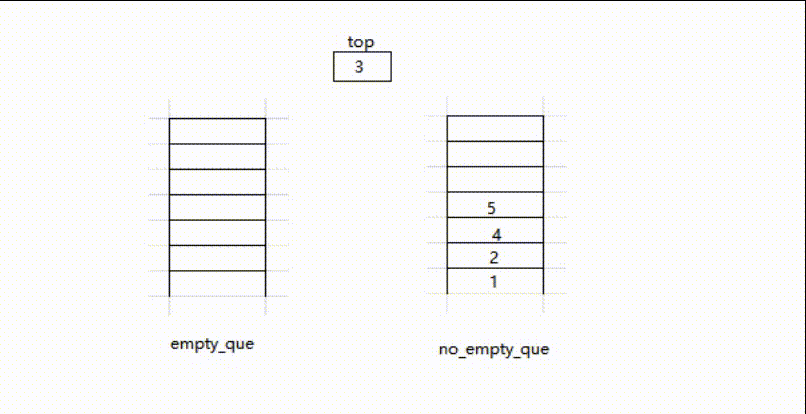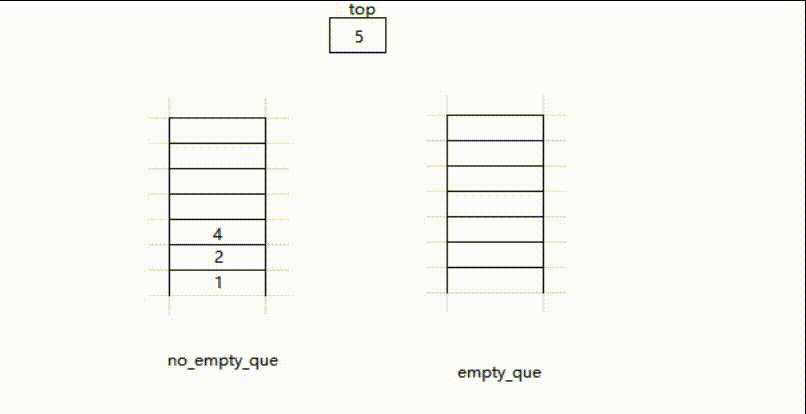
    1. 使用两个队列,一个队列no_empty_que存放已经存放的元素,另一个队列empty_que常空
    2. 当要压栈的时候,将元素压入no_empty_que
    3. 当要出栈的时候,将no_empty_que中除队尾元素全部存入empty_que,将队尾元素移出

    实例
    在这里插入图片描述

    代码实现

    typedef int QDataType;

// 链式结构表示队列
typedef struct QListNode
{
  struct QListNode* next;
  QDataType data;
}QNode;

// 队列的结构
typedef struct Queue
{
  QNode* front;    //指向队列头
  QNode* rear;     //指向队列尾
  int size;        //记录队列的元素个数
}Queue;

// 初始化队列
void QueueInit(Queue* q)
{
  assert(q);  //确保q合法

  q->front = q->rear = NULL;  //将头和为置为 NULL 
  q->size = 0;
}

// 判断队列是否为空, 如果为空返回非0, 非空返回0
int QueueEmpty(Queue* q)
{
  assert(q);  //确保q合法

  if (q->size == 0)
  {
    return 1;
  }
  else 
  {
    return 0;
  }
}

// 队尾入队列
void QueuePush(Queue* q, QDataType x)
{
  assert(q);  //确保q合法

  //创建新结点
  QNode* newNode = (QNode*)malloc(sizeof(QNode));
  newNode->data = x;
  newNode->next = NULL;

  //入队列
  if (QueueEmpty(q))
  {
    //如果队列为空,直接赋值
    q->front = q->rear = newNode;
  }
  else 
  {
    //如果队列不为空,直接尾插
    q->rear->next = newNode;
    q->rear = newNode;
  }

  q->size++;
}

// 队头出队列
void QueuePop(Queue* q)
{
  assert(q);  //确保q合法
  assert(!QueueEmpty(q)); //确保队列不为空

  if (q->size == 1)
  {
    //如果只有一个元素,头删的同时还要将尾指针置空
    free(q->front);
    q->front = q->rear = NULL;
  }
  else 
  {
    //如果不止一个元素,则只头删
    QNode* nextNode = q->front->next;
    free(q->front);
    q->front = nextNode;
  }

  q->size--;
}

// 获取头部元素
QDataType QueueFront(Queue* q)
{
  assert(q);  //确保q合法
  assert(!QueueEmpty(q)); //确保队列不为空

  return q->front->data;
}

// 获取尾部元素
QDataType QueueBack(Queue* q)
{
  assert(q);  //确保q合法
  assert(!QueueEmpty(q)); //确保队列不为空

  return q->rear->data;
}

// 获取队列元素个数
int QueueSize(Queue* q)
{
  assert(q);  //确保q合法

  return q->size;
}



// 销毁队列
void QueueDestroy(Queue* q)
{
  assert(q);

  while(!QueueEmpty(q))
  {
    QNode* nextNode = q->front->next;
    free(q->front);
    q->front = nextNode;
  }

  q->front = q->rear = NULL;
  q->size = 0;
}

//用两个队列构成一个栈
typedef struct 
{
    Queue queue1;
    Queue queue2;
} MyStack;


MyStack* myStackCreate() 
{
    MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&pst->queue1);
    QueueInit(&pst->queue2);

    return pst;
}

void myStackPush(MyStack* obj, int x) 
{
    if (!QueueEmpty(&obj->queue1))
    {
        QueuePush(&obj->queue1, x);
    }
    else
    {
        QueuePush(&obj->queue2, x);
    }
}



int myStackPop(MyStack* obj) 
{
    Queue* no_empty_que = &obj->queue1;
    Queue* empty_que = &obj->queue2;

    if (!QueueEmpty(&obj->queue2))
    {
        no_empty_que = &obj->queue2;
        empty_que = &obj->queue1;
    }

    //弹出有元素的队列直至只剩一个元素
    while (QueueSize(no_empty_que) > 1)
    {
        QueuePush(empty_que, QueueFront(no_empty_que));
        QueuePop(no_empty_que);
    }

    int pop = QueueFront(no_empty_que);
    QueuePop(no_empty_que);
    return pop;
}

int myStackTop(MyStack* obj) 
{
    if (!QueueEmpty(&obj->queue1))
    {
      return QueueBack(&obj->queue1);
    }
    else
    {
      return QueueBack(&obj->queue2);
    }
}

bool myStackEmpty(MyStack* obj) 
{
    return QueueEmpty(&obj->queue1) && QueueEmpty(&obj->queue2);
}

void myStackFree(MyStack* obj) 
{
    QueueInit(&obj->queue1);
    QueueInit(&obj->queue2);
    free(obj);
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174
    • 175
    • 176
    • 177
    • 178
    • 179
    • 180
    • 181
    • 182
    • 183
    • 184
    • 185
    • 186
    • 187
    • 188
    • 189
    • 190
    • 191
    • 192
    • 193
    • 194
    • 195
    • 196
    • 197
    • 198
    • 199
    • 200
    • 201
    • 202
    • 203
    • 204
    • 205
    • 206
    • 207
    • 208
    • 209
    • 210
    • 211
    • 212

    LeetCode232. 用栈实现队列

    题目

    你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：OJ链接

    要求

    实现 MyQueue 类：

    void push(int x) 将元素 x 推到队列的末尾
    int pop() 从队列的开头移除并返回元素
    int peek() 返回队列开头的元素
    boolean empty() 如果队列为空，返回 true ；否则，返回 false

    思路

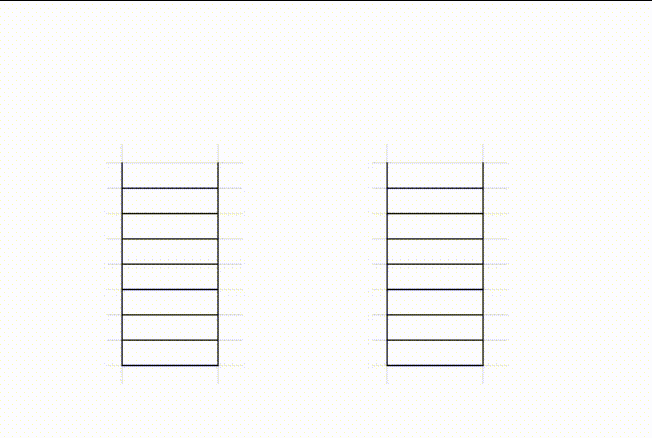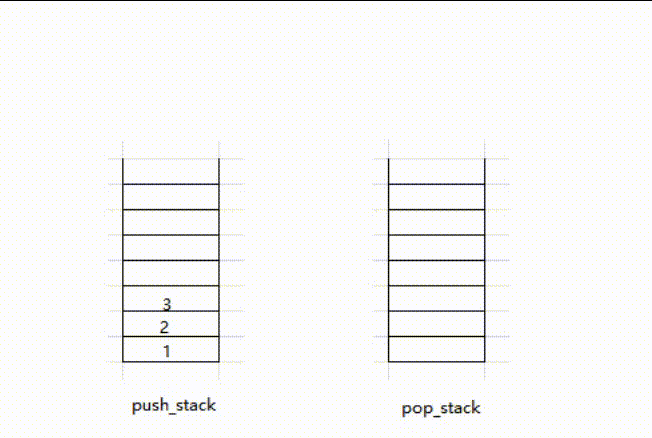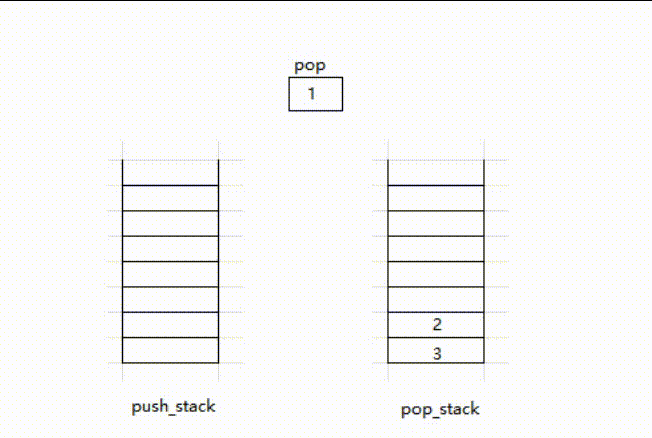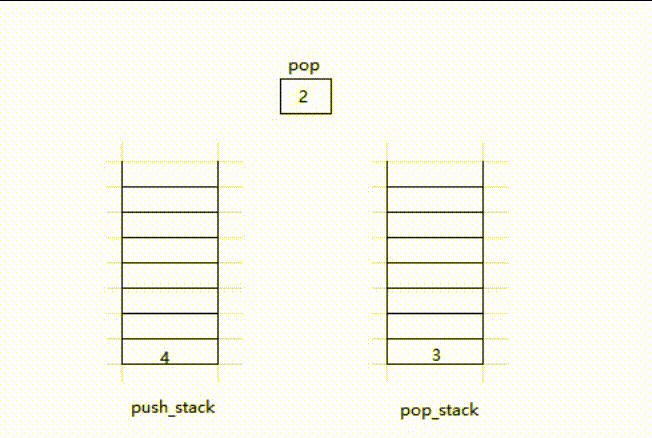
    1. 使用两个栈,一个专门负责压入数据push_stack,另一个专门负责弹出数据pop_stack
    2. 当push数据,直接将数据压入push_stack
    3. 当pop数据,如果pop_stack为空,先将push_stack中的数据压入,pop_stack,再接将pop_stack的栈顶弹出

    实例
    在这里插入图片描述

    代码实现

    typedef int STDataType;

typedef struct Stack
{
  STDataType* a;  //指向栈空间
  int top;        //栈顶
  int capacity;   //容量
}Stack;

// 初始化栈
void StackInit(Stack* ps)
{
  assert(ps);
  
  ps->a = NULL;     
  ps->top = 0;
  ps->capacity = 0;
}

//入栈
void StackPush(Stack* ps, STDataType data)
{
  assert(ps);       //确保ps合法

  //如果容量不够则扩容
  if (ps->capacity == ps->top)
  {
    int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;   //定义新的容量
    STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);  //开辟新的空间
    if (tmp == NULL)
    {
      perror("malloc error");
      exit(-1);
    }
    else 
    {
      ps->a = tmp;
      ps->capacity = newCapacity;
    }
  }

  //将数据入栈
  ps->a[ps->top] = data;
  ps->top++;
}

// 出栈
void StackPop(Stack* ps)
{
  assert(ps); //确保ps合法

  assert(!StackEmpty(ps));  //确保栈不为空
  ps->top--;

}

// 检测栈是否为空, 如果为空返回非零结果, 如果不为空返回 0
int StackEmpty(Stack* ps)
{
  assert(ps); //确保ps合法
  
  if (ps->top > 0)
  {
    return 0;
  }
  else 
  {
    return 1;
  }
}

// 获取栈顶元素
STDataType StackTop(Stack* ps)
{
  assert(ps);   //确保ps合法
  assert(!StackEmpty(ps));  //确保栈不为空

  return ps->a[ps->top - 1];
}

// 获取栈中有效元素个数
int StackSize(Stack* ps)
{
  assert(ps);   //确保ps合法
  return ps->top;
}

// 销毁栈
void StackDestroy(Stack* ps)
{
  assert(ps); //确保ps合法

  free(ps->a);
  ps->a = NULL;
  ps->capacity = 0;
  ps->top = 0;
}

typedef struct 
{
    Stack push_stack;
    Stack pop_stack;
} MyQueue;


MyQueue* myQueueCreate() 
{
    MyQueue* que = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&que->push_stack);
    StackInit(&que->pop_stack);

    return que;
}

void myQueuePush(MyQueue* obj, int x) 
{
    StackPush(&obj->push_stack, x);
}

int myQueuePop(MyQueue* obj) 
{
    int pop = myQueuePeek(obj);
    StackPop(&obj->pop_stack);

    return pop;
}

int myQueuePeek(MyQueue* obj) 
{
    //如果pop_stack是空的话,将push_stack的所有元素入pop_stack
    if (StackEmpty(&obj->pop_stack))
    {
        while (!StackEmpty(&obj->push_stack))
        {
          StackPush(&obj->pop_stack, StackTop(&obj->push_stack));
          StackPop(&obj->push_stack);
        }
    }
    //如果pop_stack不是空,直接取栈顶元素
    int peek = StackTop(&obj->pop_stack);

    return peek;
}

bool myQueueEmpty(MyQueue* obj) 
{
    return StackEmpty(&obj->push_stack) && StackEmpty(&obj->pop_stack);
}

void myQueueFree(MyQueue* obj) 
{
    StackDestroy(&obj->push_stack);
    StackDestroy(&obj->pop_stack);
    free(obj);
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156

    LeetCode622. 设计循环队列

    题目

    设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

    循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。OJ链接

    要求

    你的实现应该支持如下操作：

    MyCircularQueue(k): 构造器，设置队列长度为 k 。
    Front: 从队首获取元素。如果队列为空，返回 -1 。
    Rear: 获取队尾元素。如果队列为空，返回 -1 。
    enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
    deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
    isEmpty(): 检查循环队列是否为空。
    isFull(): 检查循环队列是否已满。

    思路

    1. 为了确保方便判断空和满情况,将循环队列的空间比设定长度加1
    2. 入队列和出队列相关front和rear不是简单的加一或减一
    3. rear指向队尾下一个空间,front指向队头元素

    代码实现

    typedef struct 
{
    int* a;     //存放队列元素
    int front;  //指向队头元素
    int rear;   //指向队尾下一个元素
    int k;      //循环队列的大小
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cq->a = (int*)malloc(sizeof(int) * (k + 1));
    cq->front = cq->rear = 0;
    cq->k = k;
    
    return cq;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front == obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    //如果满了,插入失败
    if (myCircularQueueIsFull(obj))
    {
        return false;
    }

    //如果不满,进行插入,注意rear的大小
    obj->a[obj->rear] = value;
    obj->rear = (obj->rear + 1) % (obj->k + 1);

    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    //如果没有元素,删除失败
    if (myCircularQueueIsEmpty(obj))
    {
        return false;
    }

    //直接修改front的值即可
    obj->front = (obj->front + 1) % (obj->k + 1);

    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
  • 相关阅读:
    【Lua面试】 迭代器和泛型For
    刷题记录（NC235267 星球大战，NC216012 Let‘s Play Curling，NC235294 任务，NC235569 牛可乐与NCPC）
    第五章 图
    docker使用详解
    【Maven基础概览】Maven是什么 | Maven的优势 | Maven的核心概念 | Maven的安装和使用；【分布式架构】特点介绍 | 使用Apache Kafka进行消息传递
    Prometheus认证访问-grafana配置-安装mysql和redis的节点监控
    前后端分离项目解决前端跨域访问问题
    C语言——二周目——输入输出辨析
    鸿蒙开发通信与连接：【@ohos.rpc (RPC通信)】
    linux之top、ps、free命令详解
  • 原文地址：https://blog.csdn.net/Kuzuba/article/details/132747314