垃圾回收 - 标记压缩算法

压缩算法是将标记清除算法与复制算法相结合的产物。

1、什么是标记压缩算法

标记压缩算法是由标记阶段和压缩阶段构成。
首先，这里的标记阶段和标记清除算法时提到的标记阶段完全一样。
接下来我们要搜索数次堆来进行压缩。压缩阶段通过数次搜索堆来重新填充活动对象。因压缩而产生的优点我们在介绍复制算法的时候已经说过了。不过他和复制算法不同的是，不用牺牲半个堆。

2、Lisp2算法

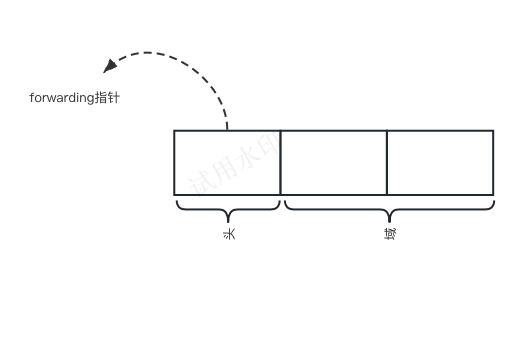
2.1 Lisp2算法中的对象

2.2 执行过程

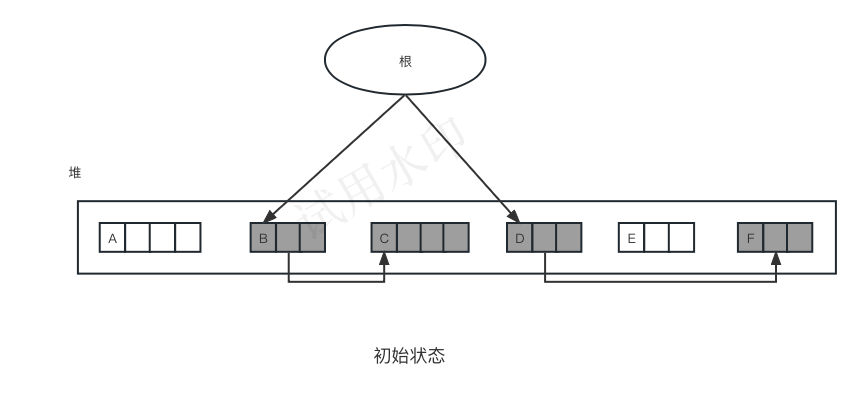
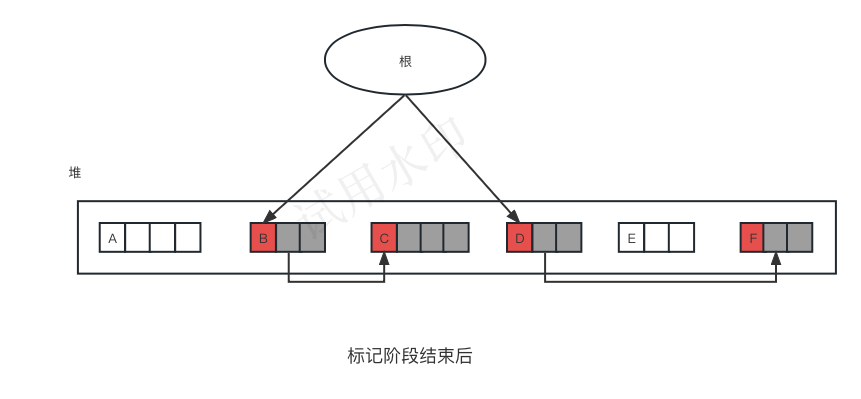
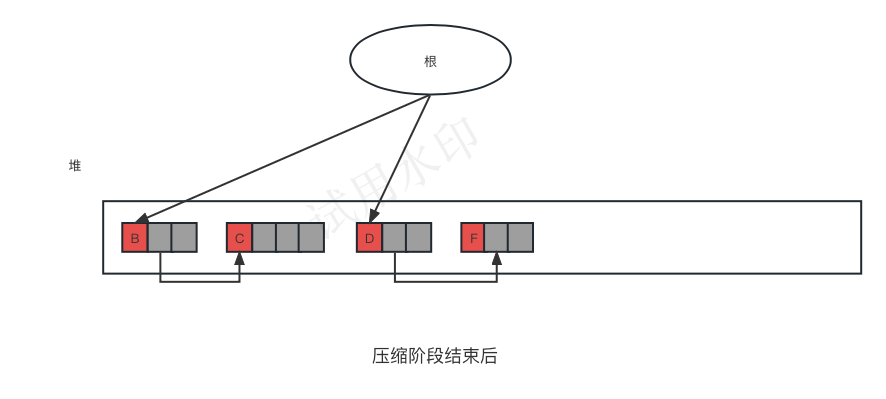
compaction_phase(){
	set_forwarding_ptr()  // 设定forwarding指针
	adjust_ptr()		//更新指针
	move_obj()          // 移动对象
}

1
2
3
4
5
6

设定forwarding指针：

set_forwarding_ptr(){
	scan = new_address = $heap_start
	while(scan < $heap_start)
		if(scan.mark == true)
			scan.forwarding = new_address
			new_address += scan.size
		scan += scan.size;
}
//scan是用来搜索堆中的对象的指针，new_address是指向目标地点的指针。
1
2
3
4
5
6
7
8
9

更新指针：

adjust_ptr(){
    //重写根的指针
   for(r : $roots)
   	*r = (*r).forwarding  

   scan = $heap_start
    //重写所有活动的指针
   while(scan < $heap_end)
   	if(scan.mark == true)
   		for(child : children(scan))
   			*child = (*child).forwarding
   	scan += scan.size;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

移动对象：

move_obj(){
   scan = $free = $heap_start
   while(scan < $heap_end)
   		if(scan.mark == true)
   				new_address = scan.forwarding
   				copy_data(new_address,scan,scan.size)
   				new_address.forwarding = NULL
   				new_address.mark = false
   				$free += new_address.size
   				scan += scan.size;
}
//本算法不会改变对象的排列顺序，只是把对象顺序从堆各处向左移动到堆的开头。因此这就保证了目标堆中已经没有活动对象了。
1
2
3
4
5
6
7
8
9
10
11
12

2.3 优缺点
优点：可有效利用堆
缺点：压缩花费计算成本。必领对整个堆进行了次搜素。也就是说，执行该算法所花费的时间是和堆大小成正比的。GC标记一压缩算法的吞吐量要劣于其他算法。

3、Two-Finger算法

3.1 前提
Two-Finger算法有着很大的限制条件，那就是必须把所有对象整理成大小一致。

3.2 执行过程

移动对象：这其中用了&free和live这两个指针，从两端向正中间搜索堆

move_obj (){
	§free = $heap_start
	live = $heap_end - OBJ_SIZE
	while (true)
		while ($free.mark == true)
			$free †= OBJ_ SIZE
		while (live.mark == false)
			live -= OBJ_SIZE 
		if ($free < live)
			copy_data ($free, live, OBJ_SIZE)
			live.forwarding = $free
			live.mark = false
		else
			break
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

更新指针：寻找移动前对象的指针，把他更新，使其指向移动后的对象

adjust_ptr () {
	for (r : $roots)
		if(*r >= $free）
			*r = (*r). forwarding
			
	scan = $heap_start
	while (scan < $free)
		scan.mark = FALSE
		for (child: children(scan))
			if (*child >= $free)
				*child = (*child) .forwarding
		scan += OBJ_ SIZE
}
1
2
3
4
5
6
7
8
9
10
11
12
13

3.3 优缺点
优点：Lisp2 算法要事先确保每个对象都留有 1个字用于forwarding 指针，这就压迫了堆。然而因为 Two-Finger 算法能把 forwarding 指针设置在移动前的对象的域里，所以不需要领外的内存空间以用于 forwarding 指针，因此在内存的使用效率上，该算法要比 Lisp2 算法的使用效率高。
此外，在Two-Finger 算法中，压缩所带来的搜素次数只有2次，比Lisp2算法少1次，在吞吐量方面占优势。
缺点：就像我们在介绍 GC 复制算法时所说的那样，将具有引1用关系的对象安排在堆中较近的位置，就能够通过缓存来提高访问速度。不过 Two-Finger 算法则不考虑对象间的引用关系，一律对其进行压缩，结果就导致对象的顺序在压缩前后产生了巨大的变化。因此，我们基本上也无法期待这个算法能沾缓存的光。
此外该算法还有一个限制条件，那就是所有对象的大小必须一致。因为能消除这个限制的处理系统不太多，所以这点制约了Two-Finger 算法的应用范围。