【算法】希尔 (Shell) 排序 详解

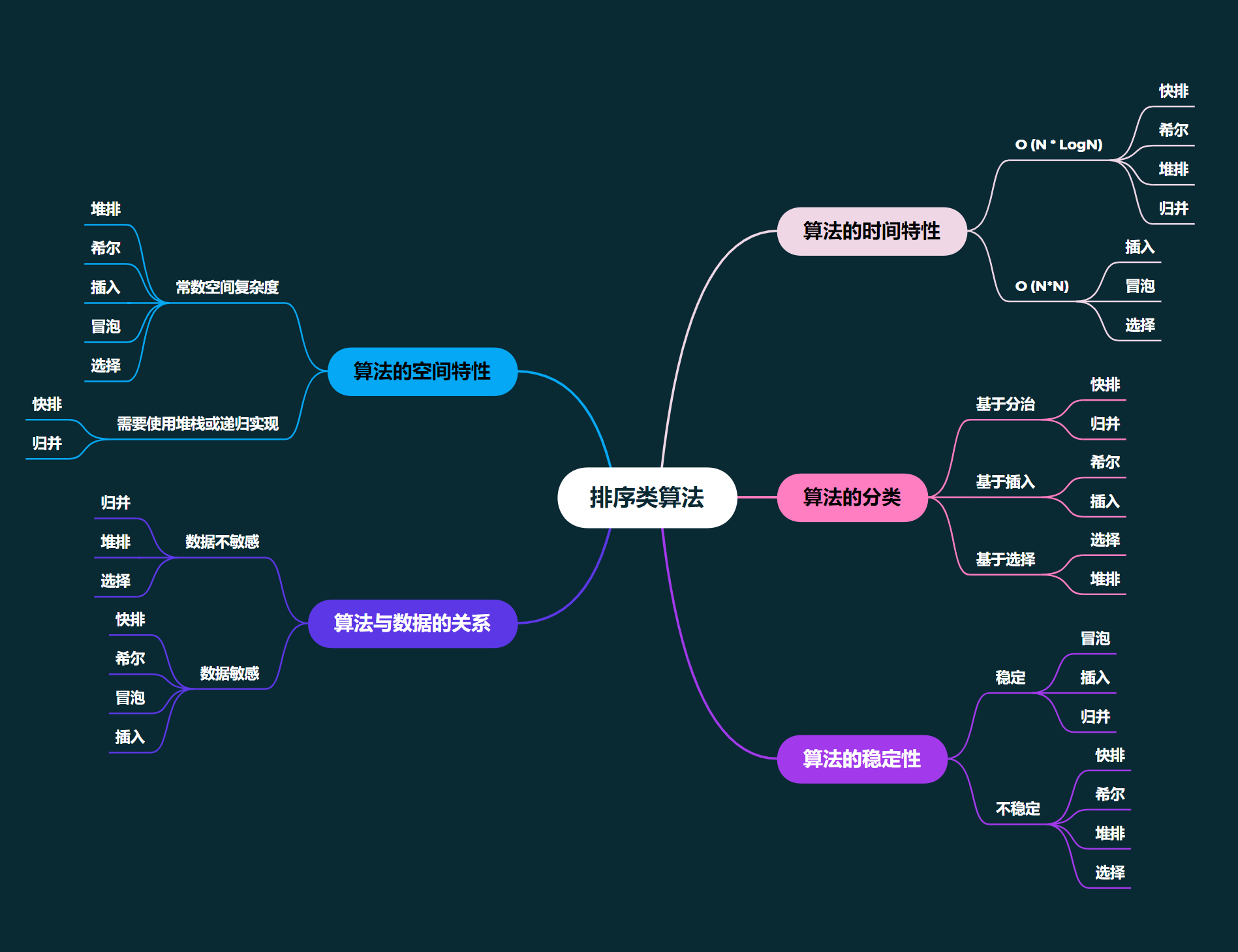
排序： 排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中， r[i] = r[j]， 且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
（注意稳定排序可以实现为不稳定的形式， 而不稳定的排序实现不了稳定的形式）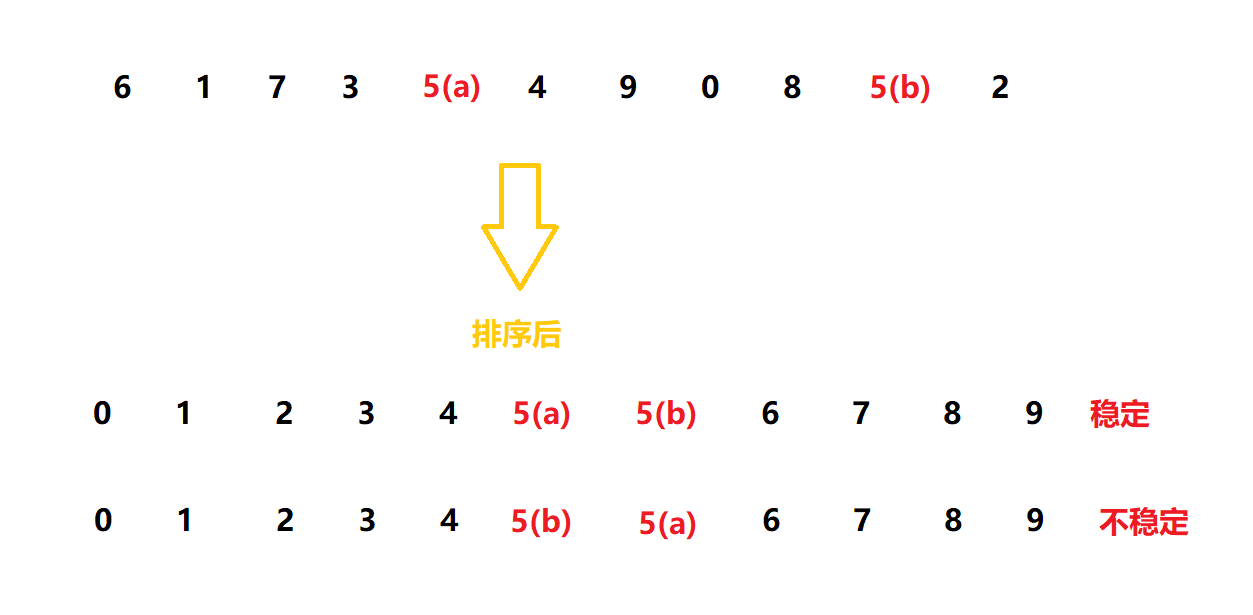

内部排序： 数据元素全部放在内存中的排序。

外部排序： 数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

希尔排序

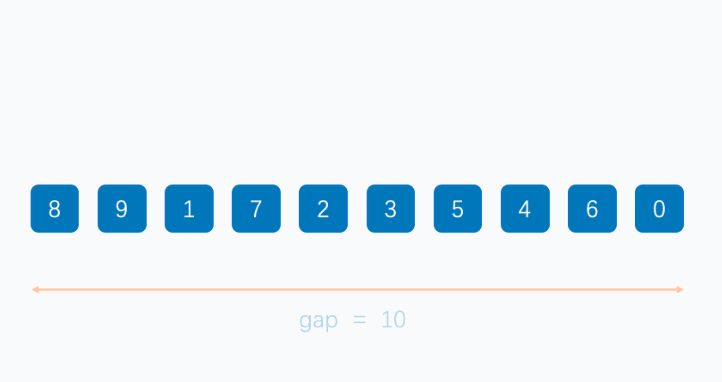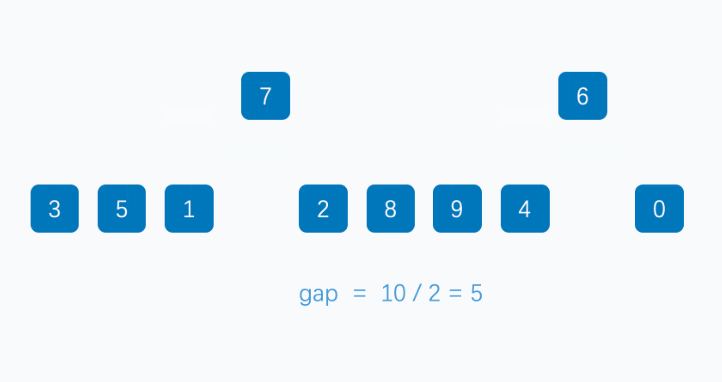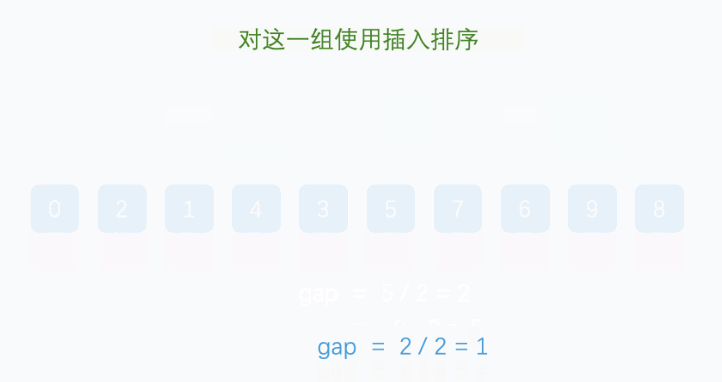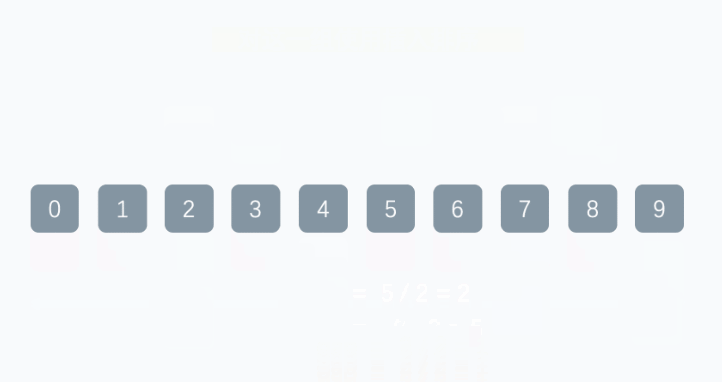
希尔排序法又称缩小增量法。希尔排序法的基本思想是：

• 选择一个增量序列（increment sequence），通常是一个递减的整数序列。常用的增量序列包括希尔增量（Shell’s increments）和Hibbard增量等。增量序列的选择会影响排序的效率。

• 对原始数据按照选定的增量值，将数据分成若干个子序列。通常是将距离为增量的元素放在同一个子序列中。

• 对每个子序列进行插入排序。插入排序是一种简单但效率较低的排序方法，但由于子序列较短，所以插入排序的性能会较好。

• 逐渐缩小增量，重复第2步和第3步，直到增量为1。当增量为1时，整个数据序列将变成一个有序序列。

最后一轮排序完成后，整个数据序列就已经有序了。

代码实现

    public static void shellSort(int[] arr) {
        int len = arr.length;
        int gap = len / 2;
        while (gap >= 1) {
            for (int i = gap; i < len; i++) {
                int key = arr[i];
                int j = i - gap;
                for (; j >= 0 && key < arr[j] ; j -= gap) {
                    // 往后挪动数据
                    arr[j+gap] = arr[j];
                }
                // 插入元素
                arr[j+gap] = key;
            }
            // 注意最终 gap 是一定要到 1 的, gap 为 1 时就是直接插入排序
            // 假如是 gap / 3 或者其他数字的话, 要 +1 不然最后到达不了 1即 gap = gap /3 + 1
            gap = gap / 2;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

总结：

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定：

• 时间复杂度： O(N^1.3) ~ O(N^1.5) (平均时间复杂度为 O(N^1.3), 近似于 O(N*logN))
• 空间复杂度： O（1）
• 是不稳定排序
• 对数据比较敏感：逆序的情况下性能有影响 (但是最坏情况不是逆序, 而是数据的分布使得每次数据都要插入到该组的最前面)

以上就是对希尔排序的讲解， 希望能帮到你 ！
评论区欢迎指正 ！