【LeetCode算法系列题解】第61~65题

LeetCode 61. 旋转链表（中等）

【题目描述】

给你一个链表的头节点 head，旋转链表，将链表每个节点向右移动 k 个位置。

【示例1】

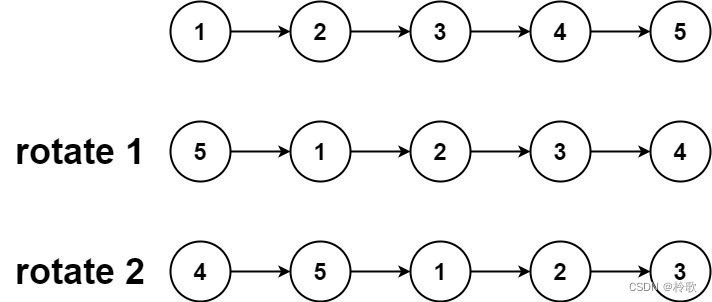
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]
1
2

【示例2】

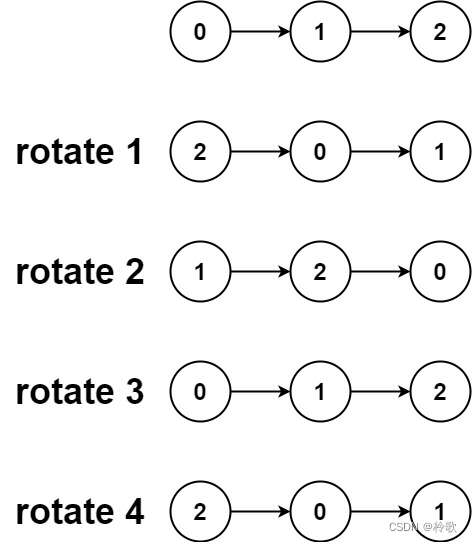
输入：head = [0,1,2], k = 4
输出：[2,0,1]
1
2

【提示】

链表中节点的数目在范围 [0, 500] 内
$-100\le Node.val\le 100$
$0\le k\le 2\ast 10^9$

【分析】

---

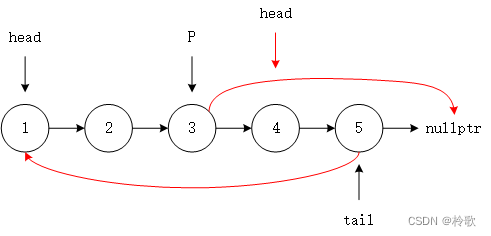
首先由于 $k$ 可能很大，当 $k$ 超过链表结点数 $n$ 时，就变成了重复的循环位移，因此 $k$ 需要先对 $n$ 取模。

以样例1为例，示意图如上图所示，算法流程如下：

• 先遍历一遍链表，求出链表长度 $n$，并记下最后一个结点 tail；
• 我们需要将链表的最后 $k$ 个结点移动到首部，因此需要先找到倒数第 $k+1$ 个结点 P，也就是正数第 $n-k$ 个结点，那么就需要从头结点向后遍历 $n-k-1$ 次；
• tail->next = head
• head = P->next
• P->next = nullptr

---

【代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if (!head) return head;  // 需要特判链表为空的情况
        ListNode* tail;
        int n = 0;
        for (auto p = head; p; p = p->next) n++, tail = p;
        k %= n;
        auto p = head;
        for (int i = 0; i < n - k - 1; i++) p = p->next;
        tail->next = head, head = p->next, p->next = nullptr;
        return head;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

LeetCode 62. 不同路径（中等）

【题目描述】

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start”）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
问总共有多少条不同的路径？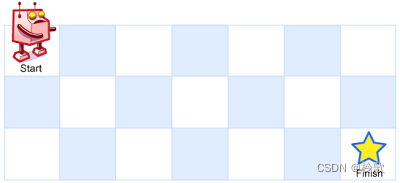

【示例1】

输入：m = 3, n = 7
输出：28
1
2

【示例2】

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
1
2
3
4
5
6
7

【示例3】

输入：m = 7, n = 3
输出：28
1
2

【示例4】

输入：m = 3, n = 3
输出：6
1
2

【提示】

$1\le m,n\le 100$
题目数据保证答案小于等于 $2\ast 10^9$

【分析】

---

本题是动态规划的数字三角形模型中的裸题，我们定义 f[i][j] 表示从起点走到点 (i, j) 的路径方案数，那么状态的转移有以下几种情况：

• 如果在第一行，那么只能从左边的点转移过来，即 f[i][j] = f[i][j - 1]；
• 如果在第一列，那么只能从上边的点转移过来，即 f[i][j] = f[i - 1][j]；
• 否则既能从左边转移过来也可以从上边转移过来，即 f[i][j] = f[i][j - 1] + f[i - 1][j]。

---

【代码】

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(m, vector<int>(n));
        f[0][0] = 1;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
            {
                if (i) f[i][j] += f[i - 1][j];
                if (j) f[i][j] += f[i][j - 1];
            }
        return f[m - 1][n - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

LeetCode 63. 不同路径 II（中等）

【题目描述】

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start”）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

【示例1】

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
1
2
3
4
5
6

【示例2】

输入：obstacleGrid = [[0,1],[0,0]]
输出：1
1
2

【提示】

$m==obstacleGrid.length$
$n==obstacleGrid[i].length$
$1\le m,n\le 100$
obstacleGrid[i][j] 为 0 或 1

【分析】

---

和上一题一样，如果 (i, j) 是障碍物，则 f[i][j] = 0，即没有办法走到这个点。如果起点或者终点是障碍物，那么直接返回 $0$ 即可。

---

【代码】

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int n = obstacleGrid.size(), m = obstacleGrid[0].size();
        if (obstacleGrid[0][0] || obstacleGrid[n - 1][m - 1]) return 0;  // 特判起点或终点就是障碍物的情况
        vector<vector<int>> f(n, vector<int>(m));
        f[0][0] = 1;
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                if (!obstacleGrid[i][j])  // 如果是障碍物f[i][j]就为0，直接跳过不计算
                {
                    if (i) f[i][j] += f[i - 1][j];
                    if (j) f[i][j] += f[i][j - 1];
                }
        return f[n - 1][m - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

LeetCode 64. 最小路径和（中等）

【题目描述】

给定一个包含非负整数的 m x n 网格 grid，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。

【示例1】

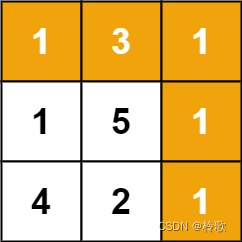
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
1
2
3

【示例2】

输入：grid = [[1,2,3],[4,5,6]]
输出：12
1
2

【提示】

$m==grid.length$
$n==grid[i].length$
$1\le m,n\le 200$
$0\le grid[i][j]\le 200$

【分析】

---

这题同样也是数字三角形模型，令 f[i][j] 表示从起点走到 (i, j) 的路径和的最小值，状态转移有如下几种情况：

• 从上边转移过来，那么结果为从起点走到 (i - 1, j) 的路径和的最小值（f[i - 1][j]）加上当前点的值，即 f[i][j] = f[i - 1][j] + grid[i][j]；
• 从左边转移过来同理，转移方程为：f[i][j] = f[i][j - 1] + grid[i][j]。

根据 f[i][j] 的定义，我们要求的是最小值，因此最终的状态转移方程为：f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j]。

---

【代码】

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> f(n, vector<int>(m, INT_MAX));  // 初始化为正无穷之后便于和自身取min
        f[0][0] = grid[0][0];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
            {
                if (i) f[i][j] = min(f[i][j], f[i - 1][j] + grid[i][j]);
                if (j) f[i][j] = min(f[i][j], f[i][j - 1] + grid[i][j]);
            }
        return f[n - 1][m - 1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

LeetCode 65. 有效数字（困难）

【题目描述】

有效数字（按顺序）可以分成以下几个部分：

1. 一个小数或者整数
2. （可选）一个 'e' 或 'E'，后面跟着一个整数

小数（按顺序）可以分成以下几个部分：

1. （可选）一个符号字符（'+' 或 '-'）
2. 下述格式之一：
   • 至少一位数字，后面跟着一个点 '.'
   • 至少一位数字，后面跟着一个点 '.'，后面再跟着至少一位数字
   • 一个点 '.'，后面跟着至少一位数字

整数（按顺序）可以分成以下几个部分：

1. （可选）一个符号字符（'+' 或 '-'）
2. 至少一位数字

部分有效数字列举如下：["2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789"]
部分无效数字列举如下：["abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"]

给你一个字符串 s，如果 s 是一个有效数字，请返回 true。

【示例1】

输入：s = "0"
输出：true
1
2

【示例2】

输入：s = "e"
输出：false
1
2

【示例3】

输入：s = "."
输出：false
1
2

【提示】

$1\le s.length\le 20$
s 仅含英文字母（大写和小写），数字（0-9），加号 '+'，减号 '-'，或者点 '.'。

【分析】

---

本题需要考虑的情况有很多种，我们一个个分析：

• e/E 的前后如果为空（在第一个或最后一个位置上），返回 false；
• xx. 或者 .xx 都是合法的，但是 .e/E 是不合法的；
• e/E 的后面如果有 .，返回 false；
• +/- 只可能在首部或者 e/E 的后面出现一次，其余地方出现均不合法；
• 如果 . 或者 e/E 出现次数大于1次则不合法；
• e/E 的后面如果是 +/-，还需要判断下一位有没有内容，如果已经到字符串末尾，也是不合法；
• 其余情况只要不是 0~9 即为不合法。

---

【代码】

class Solution {
public:
    bool isNumber(string s) {
        bool has_dot = false, has_e = false;
        if (s[0] == '+' || s[0] == '-') s = s.substr(1);
        if (s.empty()) return false;  // 字符串只有+/-
        if (s[0] == '.' && (s.size() == 1 || s[1] == 'e' || s[1] == 'E')) return false;
        for (int i = 0; i < s.size(); i++)
        {
            if (s[i] == '.')
            {
                if (has_dot || has_e) return false;
                has_dot = true;
            }
            else if (s[i] == 'e' || s[i] == 'E')
            {
                if (has_e || !i || i == s.size() - 1) return false;  // 不止一次出现E或者出现在第一个或最后一个位置
                if (s[i + 1] == '+' || s[i + 1] == '-')  // E后面是正负号还需要继续判断
                {
                    if (i + 1 == s.size() - 1) return false;
                    i++;  // 跳过正负号
                }
                has_e = true;
            }
            else if (s[i] < '0' || s[i] > '9') return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29