基于神经网络结合紫外差分光谱的二氧化硫浓度定量预测

前言

二氧化硫（SO2）是一种常见的环境污染物，对大气、水体和土壤等环境有着广泛的影响。因此，准确监测和预测大气中的二氧化硫浓度对于环境管理和污染控制具有重要意义。紫外差分光谱是一种常用于二氧化硫浓度监测的方法，通过测量大气中SO2在紫外光波段的吸收特性来进行定量分析。
本项目旨在通过应用神经网络技术，结合紫外差分光谱数据，实现对二氧化硫浓度的准确定量预测。项目将采用从不同环境中收集的紫外差分光谱数据，包括大气中SO2的光谱吸收特性以及环境参数（如温度、湿度等），作为输入特征。基于这些输入特征，将建立一个神经网络模型，通过对历史数据的学习和训练，实现对二氧化硫浓度的预测。

项目计划包括以下步骤：

1. 数据采集和准备：从不同环境中采集紫外差分光谱数据，包括SO2的光谱吸收特性以及环境参数。对采集到的数据进行处理和准备，包括数据清洗、特征提取和特征工程等。
2. 模型选择和设计：根据项目需求，选择合适的神经网络模型，并进行模型的设计。可以考虑使用常见的神经网络模型，如多层感知器（MLP）、卷积神经网络（CNN）或循环神经网络（RNN）等。
3. 模型训练和调优：使用采集到的紫外差分光谱数据，对选定的神经网络模型进行训练和调优。包括将数据集划分为训练集和验证集，进行模型参数的优化和调整，以获得最佳的预测性能。
4. 模型评估和验证：通过对模型进行评估和验证，包括使用测试数据集进行性能测试，评估模型的预测准确性、稳定性和可靠性。根据评估结果进行模型的调整和优化。
5. 结果解释和应用：根据训练好的神经网络模型，实现对二氧化硫的浓度预测

一、代码运行

本文的代码是基于百度的BML Codelab编写，项目地址：基于神经网络结合紫外差分光谱的二氧化硫浓度定量预测，数据在项目中被提供。

1. 解压数据

# 运行完一次记得注释掉
!unzip /home/aistudio/data/data208645/Data.zip -d ./data
1
2

2. 导包

import pandas as pd
import paddle
import numpy as np
from sklearn.model_selection import cross_val_score, train_test_split
import matplotlib.pyplot as plt
1
2
3
4
5

3. 读取数据

train_data = pd.read_excel("./data/Data/train.xlsx", header=None)
val_data = pd.read_excel("./data/Data/val.xlsx", header=None)
test_data = pd.read_excel("./data/Data/test.xlsx", header=None)
print("加载数据完成！")

print("train_data:",train_data)
print("val_data:",val_data)
print("test_data:",test_data)
1
2
3
4
5
6
7
8

4. 构建网络

class Regressor(paddle.nn.Layer):
    # self代表类的实例自身
    def __init__(self):
        # 初始化父类中的一些参数
        super(Regressor, self).__init__()
        
        self.fc1 = paddle.nn.Linear(in_features=423, out_features=40)
        self.fc2 = paddle.nn.Linear(in_features=40, out_features=20)
        self.fc3 = paddle.nn.Linear(in_features=20, out_features=1)

        self.relu = paddle.nn.ReLU()
    
    # 网络的前向计算
    def forward(self, inputs):
        x = self.fc1(inputs)
        x = self.relu(x)
        x = self.fc2(x)
        x = self.relu(x)
        x = self.fc3(x)
        x = self.relu(x)
        return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

5. 设置优化器

# 声明定义好的线性回归模型
model = Regressor()

# 开启模型训练模式
model.train()

# 定义优化算法，使用随机梯度下降SGD
opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
1
2
3
4
5
6
7
8

6. 模型训练

EPOCH_NUM = 20   # 设置外层循环次数
BATCH_SIZE =32  # 设置batch大小
loss_train = []
loss_val = []
training_data = train_data.values.astype(np.float32)
val_data = val_data.values.astype(np.float32)
# 定义外层循环
for epoch_id in range(EPOCH_NUM):
    # 在每轮迭代开始之前，将训练数据的顺序随机的打乱
    np.random.shuffle(training_data)
    
    # 将训练数据进行拆分，每个batch包含10条数据
    mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
    
    train_loss = []
    for iter_id, mini_batch in enumerate(mini_batches):
        # 清空梯度变量，以备下一轮计算
        opt.clear_grad()

        x = np.array(mini_batch[:, :-1])
        y = np.array(mini_batch[:, -1:])
        
        # 将numpy数据转为飞桨动态图tensor的格式
        features = paddle.to_tensor(x)
        y = paddle.to_tensor(y)
        
        # 前向计算
        predicts = model(features)
        
        # 计算损失
        loss = paddle.nn.functional.l1_loss(predicts, label=y)
        avg_loss = paddle.mean(loss)
        train_loss.append(avg_loss.numpy())
        
        # 反向传播，计算每层参数的梯度值
        avg_loss.backward()

        # 更新参数，根据设置好的学习率迭代一步
        opt.step()
    
    mini_batches = [val_data[k:k+BATCH_SIZE] for k in range(0, len(val_data), BATCH_SIZE)]
    val_loss = []
    for iter_id, mini_batch in enumerate(mini_batches):
        x = np.array(mini_batch[:, :-1])
        y = np.array(mini_batch[:, -1:])
        
        features = paddle.to_tensor(x)
        y = paddle.to_tensor(y)
        
        predicts = model(features)
        loss = paddle.nn.functional.l1_loss(predicts, label=y)
        avg_loss = paddle.mean(loss)
        val_loss.append(avg_loss.numpy())
    
    loss_train.append(np.mean(train_loss))
    loss_val.append(np.mean(val_loss))

    print(f'Epoch {epoch_id}, train MAE {np.mean(train_loss)}, val MAE {np.mean(val_loss)}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

7. 可视化loss

# loss
x = np.linspace(0, EPOCH_NUM+1, EPOCH_NUM)

plt.figure()
plt.plot(x, loss_train, color='red', linewidth=1.0, linestyle='--', label='line')
plt.plot(x, loss_val, color='y', linewidth=1.0, label='line')
plt.savefig('loss.png', dpi=600, bbox_inches='tight', transparent=False)
plt.legend(["train MAE", "val MAE"])
plt.title("Loss")
plt.xlabel('epoch_num')
plt.ylabel('loss value')
1
2
3
4
5
6
7
8
9
10
11

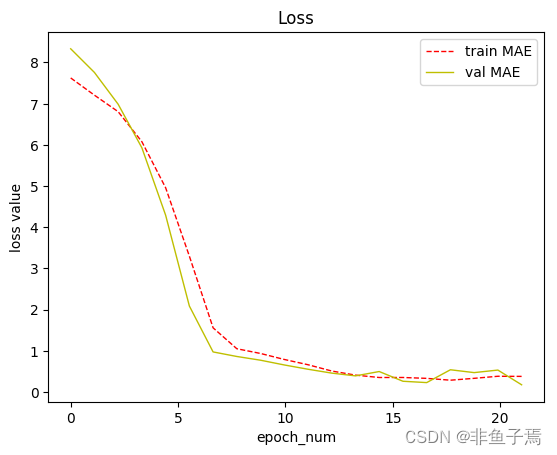
8. 模型验证

model.eval()
test_data = paddle.to_tensor(test_data.values.astype(np.float32))
test_predict = model(test_data)
test_predict = test_predict.numpy().flatten()
test_predict = test_predict.round().astype(int)
print("test_predict:",test_predict)
1
2
3
4
5
6

二、结果展示

x = np.linspace(0, 10, 9)
Y_test = [4,9,5,6,7,14,12,13,15]
Y_test = np.array(Y_test)

predicted = test_predict
plt.figure()
plt.scatter(x, predicted, color='red')  # 画点
plt.scatter(x, Y_test, color='y')  # 画点
plt.plot(x, predicted, color='red', linewidth=1.0, linestyle='--', label='line')
plt.plot(x, Y_test, color='y', linewidth=1.0, label='line')
plt.savefig('result.png', dpi=600, bbox_inches='tight', transparent=False)
plt.legend(["predict value", "true value"])
plt.title("SO2")
plt.xlabel('X')
plt.ylabel('Absorption intensity')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

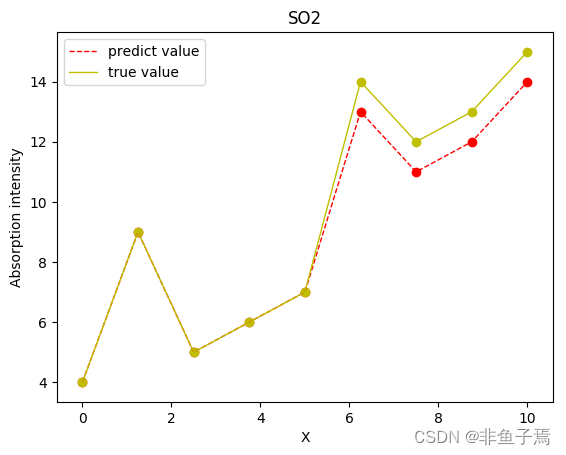
三、总结

• 从图中我们可以看出，在SO2高浓度的时候，预测的不是很准确，这大概率是因为非线性的影响。
• 在气体浓度定量分析中，如何去除非线性的影响，是一直研究的课题。
• 可以加入光谱预处理来提高模型的准确性
• 例如可以对数据进行差分拟合、小波变换、傅里叶变换等来改进

作者简介

CSDN 人工智能领域新星创作者

百度飞桨开发者技术专家

腾讯云开发初级工程师认证

我在AI Studio上获得钻石等级，点亮9个徽章，来互关呀~