算法笔记：平衡二叉树

1 介绍

• 平衡二叉树（AVL树）是一种特殊的二叉搜索树（BST），它自动确保树保持低高度，以便实现各种基本操作（如添加、删除和查找）的高效性能。
  • ——>时间都维持在了O(logN)
• 它是一棵空树，或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

• 平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入删除的时候平衡二叉树的平衡可能被改变

2 插入

• 把需要重新平衡的结点叫做α（下图中的6）
• 由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.
• 容易看出，这种不平衡可能出现在下面4中情况中：

  • 1.对α的左儿子的左子树进行一次插入

    2.对α的左儿子的右子树进行一次插入

    3.对α的右儿子的左子树进行一次插入

    4.对α的右儿子的右子树进行一次插入

    • 
  • 情形1和情形4是关于α的镜像对称，二情形2和情形3也是关于α的镜像对称
    • ——>因此理论上看只有两种情况
      • 外：左左（左孩子的左子树长）、右右（右孩子的右子树长）
      • 内：左右、右左

2.1 单旋转

2.1.1 左旋转

左旋转的基本步骤如下：

1. 首先创建一个新节点 ，该节点的值设为根节点的值；
2. 新节点的左指针指向根节点的左子树；
3. 新节点的右指针指向根节点的右子节点的左子树；
4. 将根节点的值设置为根节点的右子节点的值；
5. 根节点的左指针指向新节点；
6. 根节点的右指针指向其右子节点的右子树。

比如我们插入8：

显然此时不是平衡二叉树，我们进行左旋转调整

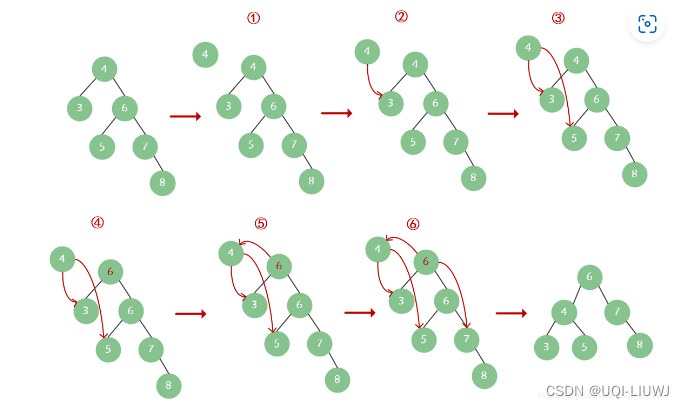
于是得到了一棵二叉树

2.1.2 右旋转

右旋转基本步骤如下：

1. 首先创建一个新节点，新节点的值设为根节点的值；
2. 新节点的右指针指向根节点的右子树；
3. 新节点的左指针指向根节点的左子节点的右子树；
4. 将根节点的值设为其左子节点的值；
5. 根节点的左指针指向其左子节点的左子树；
6. 根节点的右指针指向新节点。

比如我们插入一个1

显然此时不是平衡二叉树，我们进行右旋转调整

2.2 双旋转

对于左右和右左两种情况，单旋转不能解决问题，要经过两次旋转

首先以K1为根，做一次左旋转；

然后以K3为根，做一次右旋转

2.2.1 判断是否需要双旋转

双旋转代码的核心思想在于：在创建二叉树的过程中，每次添加新的节点，都要判断一下该二叉树是否需要旋转。

• 如果二叉树需要左旋，则先判断根节点的右子节点的左子树高度是否大于右子树的高度，如果大于则先对根节点的右子树进行右旋，最后再对原二叉树进行左旋；
• 如果二叉树需要右旋，则先判断根节点的左子节点的右子树高度是否大于左子树的高度，如果大于则先对根节点的左子树进行左旋，最后再对原二叉树进行右旋。

左子树的右子树大——先左子树旋转，再整体旋转

右子树的左子树大——先右子树旋转，再整体旋转

3 删除

同插入操作一样，删除结点时也有可能破坏平衡性，这就要求我们删除的时候要判断是否进行平衡性调整

3.1 删除根结点

• 如果左右子树都非空。在高度较大的子树中实施删除操作

  • 左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后删除左子树中元素值最大的那个节点

  • 左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后删除右子树中元素值最小的那个节点。

3.2 删除的时候进行旋转调整

参考内容：平衡二叉树详解 - zhangbaochong - 博客园 (cnblogs.com)

平衡二叉树（AVL树）_RonzL的博客-CSDN博客