KMP 算法详解

 

1 KMP算法解决的问题

字符串str1和str2，str1是否包含str2，如果包含返回str2在str1中开始的位置。并做到时间复杂度为 $O(n)$

---

 

2 前缀问题

 

求一个字符串中每个字符前缀和后缀相等的最大长度

比如求字符串 :

a b b a a b b a b b a a b b a k l

假设此时来到的位置为 i

求解方法如下:

先看i - 1 位置的 前缀和后缀相等的最大长度 CN ;

比较 CN 位置和 i - 1位置的字符串是否相等,如果相等,则i位置的前缀和后缀相等的最大长度为 CN + 1;

---

为什么CN + 1位置是前缀和后缀相等的最大长度呢? 以下来看证明 ,假设有字符串
c f g d c f g d a c f g d c f g d a f

第17个位置的字符a的前缀和后缀相等的最长子串是c f g d c f g d 即前缀和后缀相等的长度为8,接下来按上面描述的算法计算第18个字符f前缀和后缀相等的最大长度,f前一个字符a和a的前缀和后缀相等的最大长度8所在的字符a相等,所以f的前缀和后缀相等的最大长度为 9(8+1) 即如下图所示
 

 

那是否能找到比9更长的字符串呢,这里先假设可以找到
 

 

如图中所示,如果可以找到比9更长的前缀和后缀相等的最大长度,那i位置要向后移动,j位置要向前移动,则此时会发生什么呢,字符a前缀和后缀相等的最大长度将增大,这与我们之前求出的a位置的前缀和后缀相等的最大长度是矛盾的,因此假设不成立,进而证明不能找到比9更长的;

---

 

如果不相等,得到 CN位置的前缀和后缀相等的最大长度CN,继续用CN位置的字符和 i - 1位置的字符比较

---

示意图如下 :

假设我们求的是第16位置的字符 f 前缀和后缀相等的最大长度,因为前一个字符 c前缀和后缀相等的最大长度是7,所以比较下标7的字符r和下标15的字符c,很不巧,不相等,按照上面的算法,此时要使用下标7的字符r前缀和后缀的相等的最大长度3所在的字符和15位置比较,如下图所示 :

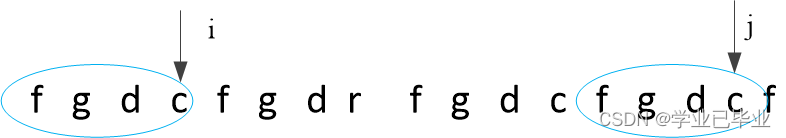
那巧啦,图中 i 位置的字符和 j 位置的字符相等,则f位置的前缀和后缀相等的最大长度为 4

为什么直接比i位置和j位置就可以了呢,原因如图所示:
由f的前一个字符c的前缀和后缀相等的最大长度 有如下结论:

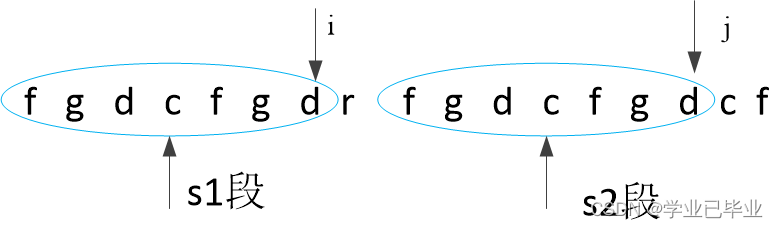
图中 s1段和s2段的字符一定是一一对应相等的

继续–>
样例字符串中下标7的字符r前缀和后缀相等的最大子串是 fgd

由上面的结论结合图示,可以得出s2段和s4段相等,s1段和s2段相等,所以s1段和s4段相等,因此只需比较s1段和s4段各自的后一个字符是否相等即可

---

循环上述过程,碰到CN为0,则i位置的 前缀和后缀相等的最大长度为0

获取一个字符串中所有字符前缀和后缀相等的最大长度代码实现

coding

/**
  *
  * @param m 获取字符数组m每一个位置 前缀和后缀相等的最大长度
  * @return
  */
 public static int[] getNextArr(char[] m){
     if (m.length == 1){
         return new int[]{-1};
     }
     int[] retArr = new int[m.length];
     // 规定 0 位置 前缀和后缀相等的最大长度为 -1
     retArr[0] = -1;
     // 规定 1 位置 前缀和后缀相等的最大长度为 0
     retArr[1] = 0;

     // 使用字符数组中那个位置的字符与 i - 1 位置的字符进行比较
     int cmpIndex = 0; // i - 1位置的字符前缀和后缀相等的最大长度
     // i在2位置时,使用i - 1位置的,即 1位置的字符前缀和后缀相等的最大长度
     // 初始时,使用 0 位置的字符和1位置的字符比较
     int i = 2;
     while (i < m.length){
         // cmpIndex位置字符和i位置的字符相等 
         // 则i位置的前缀和后缀相等的最大长度为cmpIndex+1
         if (m[cmpIndex] == m[i - 1]){
             retArr[i++] = ++cmpIndex;
         } else if (cmpIndex > 0){
             cmpIndex = retArr[cmpIndex];
         } else {
           retArr[i++] = 0;
         }
     }
     return retArr;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

C 语言版

int32 *getNextArr(char *str, int nextArr[], int strLen)
{
    if (strLen == 1)
    {
        nextArr[0] = -1;
        return nextArr;
    }

    nextArr[0] = -1;
    nextArr[1] = 0;
    int32 index = 2;
    int preIndex = 0;
    while (index < strLen)
    {
        if (str[index - 1] == str[preIndex])
        {
            str[index++] = preIndex++;
        }
        else if (preIndex > 0)
        {
            preIndex = nextArr[preIndex];
        }
        else
        {
            nextArr[index++] = -1;
        }
    }
    return nextArr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3 KMP 算法

coding

假设 S1是较长的字符串,S2是较短的字符串,

暴力匹配法 :
S1从第一个字符开始和S2中的字符一一比较,发现不相等则继续使用下一个位置的字符开始和S2中的字符进行比较

int32 getIndex(char* s1,char* s2)
{
    if (s1 == NULL || s2 == NULL || strlen(s2) < 1 || strlen(s2) > strlen(s1))
    {
        return -1;
    }
    
    int32 i1 = 0;
    int32 i2 = 0;

    int32 L1 = strlen(s1);
    int32 L2 = strlen(s2);
    int retIndex = 0;
    
    while(i1 < L1 && i2 < L2)
    {
        if(s1[i1] == s2[i2])
        {
            i1++;
            i2++;
        }
        else
        {
          i1 = (retIndex ++) + 1;
          i2 = 0;   
        } 
    }
    return i2 == L2 ? retIndex : -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

KMP算法也是 一一匹配,只是有加速
 
具体图解如下 :

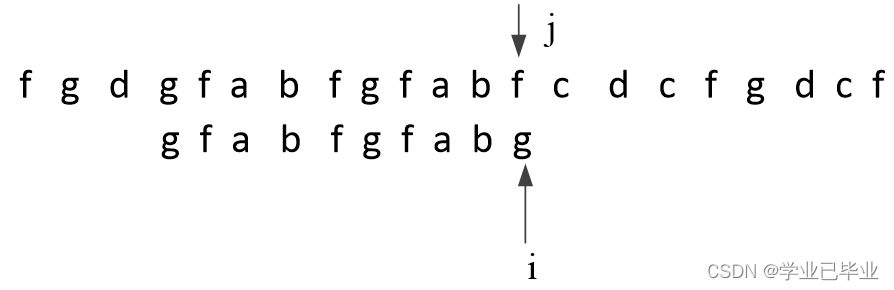
图中S1到了j,S2到了i位置发现字符串不相等

KMP的做法如下 :

S1在j位置不动,i回到i位置前缀和后缀相等的最大长度处 如图 :

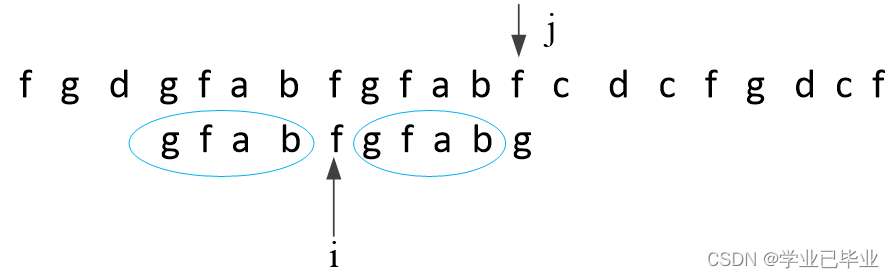
即 i位置和 j位置继续进行比较

如此做法是为啥呢? 看证明 :

首先证明字符 S2 i 位置之前的字符和 字符 S2 j位置之前的字符是比较过的

还是继续来看上一步的比较结果 得出

 

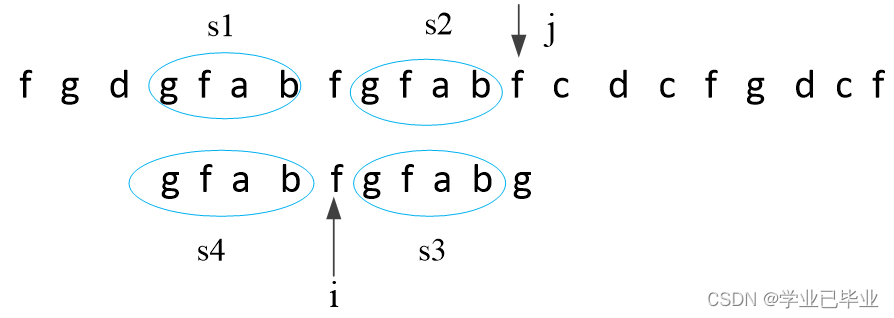
s2段和s3段是一一对应相等,再由g字符的前缀和后缀相等的最大长度得出s4段和 s3段是一一对应相等的,进而可得出 s4段和 s2段是相等的

然后在证明g到f之间是配不出s2的 即 k,j之间是配不出s2的
 

 

使用反证法,假如 k 和 j之前可以配出来 :

图中已知的信息如下 :
子串str2从0位置到 Y - 1位置都和 str1 的 i位置到 X -1 位置一一对应相等

假设 str1 的 i j之间的位置 k可配出 str2 则会出现图中所示的情况

从图中可以明显的看出 str1 k位置 到 X - 1位置 和 字符和字符串 str2从0位置开始等量的段相等,在由已知信息可以得出如下结论 :
得到 str2字符串前缀和后缀相等的最大长度为 k 到 X - 1 ,明显这段是大于s2段的长度,这是不可能的,因此证明了 i和j之间是配不出来的

 
 

/**
  * KMP算法解决的问题
  * 字符串str1和str2，str1是否包含str2，如果包含返回str2在str1中开始的位置。
  * 如何做到时间复杂度O(N)完成？
  * 字符串1的长度是M
  * 字符串的长度是N
  * 暴力匹配的时间复杂度O(M * N)
  * 前缀和后缀相等的最大长度
  * 前缀和后缀不能取到整体
  *
  */
 public static int getIndex(String s1,String s2){
     if (s1 == null || s2 == null || s2.length() < 1 || s2.length() > s1.length()){
         return -1;
     }

     char[] str1 = s1.toCharArray();
     char[] str2 = s2.toCharArray();

     int[] nextArr = getNextArr(str2);
     int i1 = 0;
     int i2 = 0;
     while (i1 < str1.length && i2 < str2.length){
         if (str1[i1] == str2[i2]){
             i1++;
             i2++;
         } else if (nextArr[i2] == -1){//第一个字符
            i1 ++;
         } else {
             // i2直接到 i2位置前缀和后缀相等最大长度的位置
             i2 = nextArr[i2];
         }
     }
     // 只有 i1 == str2.length时才匹配成功 否则str2就不在str1中
     return i2 == str2.length ? i1 - i2 : -1;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

c++ 版本
 

void getNextArr(std::string& str,int* nextArr)
{
    if(str.length() == 0)
    {
    	return;
    }
    nextArr[0] = -1;
    nextArr[1] = 0;
    int preIndex = 0;

    for (int i = 2; i < str.length();)
    {
         if (str[i - 1] == str[preIndex])
         {
             nextArr[i++] = ++preIndex;
         }
         else if (preIndex > 0)
         {
              preIndex = nextArr[preIndex];
         }
         else
         {
             nextArr[i++] = 0;
         }
    }
}

int getIndex(std::string& s1,std::string& s2)
{
     if(&s1 == NULL || &s2 == NULL || s2.length() < 1 || s1.length() < s2.length())
     {
         return -1;
     }

     int* pNextArr = new int[s2.length()];

     getNextArr(s2,pNextArr);

     int i1 = 0;
     int i2 = 0;

     while(i1 < s1.length() && i2 < s2.length())
     {
          if(s1[i1] == s2[i2])
          {
              i1++;
              i2++;
          }
          else if (pNextArr[i2] == -1)
          {
                i1 ++;
          }
          else
          {
               i2 = pNextArr[i2];
          }
     }

     delete[] pNextArr;
     return i2 == s2.length() ? i1 - i2  : -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61