哈喽大家好,我是咸鱼
之前看到过耗子叔写的一篇文章《程序算法与人生选择》,这篇文章中耗子叔结合计算机中的经典算法(排序、动态规划等等),让大家在人生道路的选择上获得了一些启发
我最近看了一些关于贝叶斯思想的文章,觉得还挺有感触的,于是打算写一篇相关的文章
今天这篇文章不会跟大家讲贝叶斯公式的推导
而是介绍什么是贝叶斯思想,以及如何结合贝叶斯思想为自己的人生规划做决策
前言
贝叶斯思想是由英国数学家和统计学家托马斯·贝叶斯(Thomas Bayes)提出的
托马斯·贝叶斯生活于 18 世纪,他的主要贡献是在概率理论领域。尽管贝叶斯自己并没有将其思想形成完整的理论,但他的名字被用于描述一类基于条件概率的推理方法,即贝叶斯方法
贝叶斯将概率解释为一种表示不确定性或信念的度量,而不仅仅是频率的统计概念
关于贝叶斯思想,有两个概念需要大家知道:
- 先验概率(Prior Probability):先验概率是在考虑任何观察数据之前,基于经验、先前知识或主观判断所获得的概率。它表示对事件发生的初始信念或先前的估计
- 后验概率(Posterior Probability):后验概率是在考虑观察数据之后,通过使用贝叶斯定理计算得到的概率。它表示在观察到新的数据后,对事件发生概率的修正和更新
贝叶斯思想的核心就是通过结合先验知识(先验概率)和新的观察数据来更新和修正我们的信念(后验概率)
频率学派认为:概率是事件在一段时间内发生的频率。不参照过去的经验,只按照当前已有的数据进行概率推断
例如你一直扔一个标准的硬币,你得到正面的概率永远是 50%
贝叶斯派认为:概率是我们对一件事情发生的相信程度(信念度)。换句话说,发生某件事情的概率越大,表明我们对这件事情发生的信心越大
1968 年 6 月,天蝎号核潜艇在大西洋亚速海海域失踪了,潜艇上的 99 名海军官兵全部杳无音信
对于搜寻人员来讲,无异于大海捞针。海军请来了科学家 John Craven 来组织搜寻,下面是他搜寻的步骤:
- John Craven 列出了一系列能够解释这场事故的场景
- 接着,他组建了了一个由各个领域专家组成的团队,让每个成员提供自己对每个可能场景发生概率的猜测
- 然后将整个海域被分成了很多个小格子,每个小格子有两个概率值 p 和 q,p是潜艇躺在这个格子里的概率,q 是如果潜艇在这个格子里,它被搜索到的概率
- 每次寻找时,先挑选整个区域内潜艇存在概率值最高的一个格子进行搜索
- 如果没有发现,概率分布图则会被“洗牌”一次,搜寻船只就会驶向新的“最可疑格子”进行搜索,这样一直下去,直到找到天蝎号为止
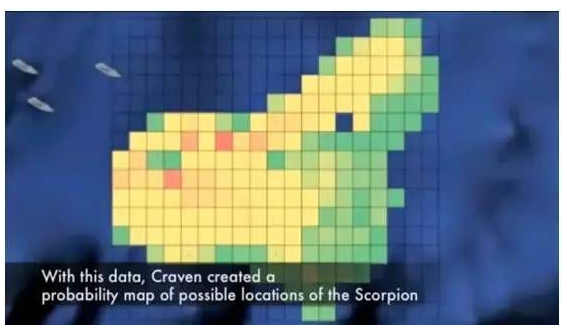
John Craven 采用的正是贝叶斯法——先根据先前的常识、经验进行预测得到先验概率然后进行搜索
每一次没搜到都不会被浪费,也不是简单被标注为不在这里,而是用于更新调整整体的估算概率(后验概率)
贝叶斯算法
当我们在面临人生的选择,又或者在进行人生规划的时候,我们可以结合贝叶斯思想来指导我们做决策
要点一:拥抱不确定性
贝叶斯思想告诉我们,概率是一种主观的信念,并且这个概率会随着后续更多的信息不断更新
这个概率不断更新的过程,其实就是不断尝试、不断接受新信息的过程
我们想要做抖音,想要打造个人 IP,但是我们又担心万一自己辛苦一番,后面要是抖音这些自媒体不吃香了怎么办?
我们打算考研,但是我们又不知道自己能不能考得上,万一辛苦备考一年考不上该咋办?
说到底就是害怕不确定性。确保成功是很多人做决定的前提,但是我们要知道,这个世界上并没有什么事情是确定的
而贝叶斯思想告诉我们,在做一件事情之前(自媒体、考研),可以先有一个大概的评估(自媒体是否还是风口,自己过去的学习成绩怎么样),这个评估就是先验信念
然后就是先干起来再说,不要害怕不确定性、害怕错误,然后在这个过程中不断地更新自己的后验信念,调整策略
越是追求确保成功的人,反而越脆弱,越容易掉入决策的陷阱,越容易上别有用心的人的当
例如,市面上的种种骗术都是以“确保成功”为吸引点的
要点二:重视基础概率
贝叶斯思想中有两个概率——先验概率和后验概率
但还有一个概率我们需要知道——基础概率
基础概率是关于一个类别、事件或条件的总体频率,是没有任何额外信息的情况下的概率
基础概率也可以被看作是一种特殊的先验概率,即没有任何特定证据的先验概率
我们要重视基础概率,例如去鱼多的地方捕鱼,鱼多就是一个基础概率
中国的首富一直是农夫山泉的老板。一个重要的原因是:2022年中国饮料市场约为12478 亿,其中包装饮用水占比约为 62.7%,基数够大,基础概率够大
选择比努力更重要这句话也表明我们要重视基础概率
就业方面是选择夕阳行业还是新兴行业?投资方面是看重局部时间的涨跌概率还是看重长期的基本面?填志愿是选择王牌专业还是冷门专业?
要点三:对新信息保持“敏感”,又有独立判断的“钝感”
虽然贝叶斯派认为概率是主观的,但是并不意味着贝叶斯派是一群主观的人
相反,他们随时打算更新自己的观点
哪怕新的信息(证据)和自己的信念相反,哪怕消息很让人恼火,很羞辱自己的智商,贝叶斯派们也坦然接受。
但是他们又不是简单的见风使舵,他们不会因为新信息彻底抛弃旧的信念,还需要结合先验概率来独立判断
- 对新信息保持“顿感”
例如,我们拥有的某支股票近期波动较大,当我们看到某些看空的评论时,我们应该更新对这支股票的评估
- 考虑基础概率和先验概率,独立判断的“钝感”
对于这支股票,无论是市场政策还是其公司经营情况都是利好的(先验概率),那么即使我们收到了一些利空的信息或评论,也不能够立即得出股票需要抛出的结论
我们还需要权衡初步信念(长期看好这支股票)和新的证据(利空评论)
这样的平衡不但使我们对新信息保持敏感,又能保持我们对初步信念的忠实,避免被一些可能的偶然事件或者噪音误导
总结
这个世界充满不确定性,我们需要拥抱不确定性,拥抱风险,要用逐步消除不确定性来接近确定性,而不是用确定性来证明确定性
在进行人生规划时,我们可以先基于自己的常识、经验和当前的信息来评估自己的决策。然后先干为敬,并在这个过程中不断地试错,以此来动态调整自己的决策
我们还需要重视基础概率,做成功的基础概率大的那个决策
最后,当有新信息出现的时候,我们需要开放接受,但也需要独立判断,既不盲目跟从,也不闭目塞听