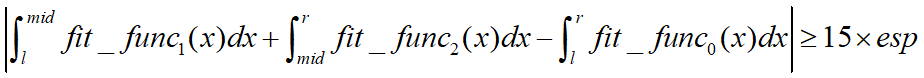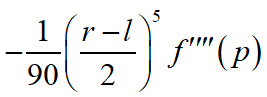引子
有时候我们需要计算一个函数的定积分，粗略上可以使用估算的方法。如图所示，将原本的曲线粗略地看成一个梯形。这个方法叫梯形法则（Trapezoidal Rule）。也叫做一阶牛顿-柯特斯闭型积分公式。
其中
所谓一阶，指的就是n=1的情况。
最理想的情况就是把这个图像分割成 无数 个梯形，便可求出对应的定积分。
但是在实际操作的情况下，梯形法则为了保证速度无法取极多的点，这样照成梯形法则误差较大。
分割成无限个梯形其实就等效于
因此我们将考虑更高阶的公式，本文将要介绍的便是二阶牛顿-柯特斯闭型积分公式（辛普森法）。 即将函数近似看成一条抛物线。显然一阶牛顿-柯特斯闭型积分公式需要在首尾取两个点方可得到f(x)的解析式。而二阶要得到一个抛物线方程则需要取三个点，才能得到解析式。而牛顿-柯特斯闭型积分公式都采用等距取点的方法，所以辛普森法需要取首尾点以及中间点。
推导方法
通过辛普森法，只需要计算出边界和中点的函数值就可以得到估算的函数的积分
绿色是被积函数，红线是使用梯形法则得到的，蓝线是辛普森法得到的。可以发现相对梯形法则，辛普森法相对而言更符合被积函数。继续提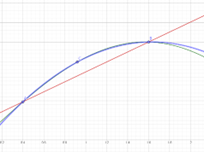
高n的值可以提高估算的准确度，但显然也会提高计算的复杂性，而二阶的对于图中的函数基本上可以达到要求。
对于一段基本符合二次函数的函数，辛普森法可以得到较为准确的结果，然而当函数变得复杂时。辛普森将出现明显的误差。这时候该怎么计算积分。
摆在面前的有两条路，一个是不断细分区间，再将区间求和，另一条是增加n的值，使得函数更加符合被积函数。本文主要讨论第一种方法。
正文
走第一条路，如果采用将区间平均细分为若干份，求得各个区间的积分后再统一求和，这样在计算量上和梯形法则上相等，但是精度提升不了多少。
然而，不得不承认，对于一个函数而言，存在二次拟合比较好的地方，也存在比较差的地方。如果在拟合比较好的地方细分就会浪费计算资源，而统一的平均细分，也导致在拟合比较差的地方达不到想要的精度。
因此，如何在拟合好的地方降低细分程度，拟合差的地方提高细分进度成了重中之重。
而本文想介绍的关键自适应辛普森积分法，就是解决这个问题的。
上式是自适应辛普森积分法是否对一个区间进行细分的判定条件。
其实是根据这个结论：
原理其实很简单，首先将这个区间进行二分为两个区间肯定能得到更为精准的结果，如果这个结果和直接计算该区间的辛普森积分得到的结果差距大于某一个值，则认为对这个区间继续细分是有意义的，反之差距小于该值则说明继续细分对提高精度没有什么帮助，就不进行下一步的细分，以降低计算的复杂度。这个值一般是esp的15倍（至于为什么是15倍可以看看这篇文章Notes on the Adaptive Simpson Quadrature Routine），调节esp可以控制估计值和精确值在多少位前是一样的。
扩展：为什么二分一个区间能够得到一个更精确的结果，从图像上很好理解，两个函数要比一个函数拟合得更紧密。从数值上说明是因为辛普森算法的误差公式为
p是f(x)在[l,r]区间内使得f(x)四阶导数取得最大值的值。具体证明可以参考A short proof of the error term in Simpson's rule（看不懂？本笔者也看不懂）。根据琴生不等式可以推导出区间一分为二后的误差和小于不一分为二的误差（大概可以证明吧，以后有时间证明一下QAQ）。
据说（美）萨奥尔（Sauer, T.）著；裴玉茹，马赓宇译.数值分析（原书第2版），机械工业出版社，第240页。 有相对完善的介绍，以后买一本看看。
代码
#include #include #include using namespace std; double F(double x) { return x * log(x); } double PF(double x) { return 1.0 / 2.0 * x * x * log(x) - 1.0 / 4.0 * x * x; } //primitive function: 1/2xlnx-1/4x int count_simpson =0; double simpson(double l,double r) { count_simpson++; return (r - l) / 6.0 * (F(l) + F(r) + 4 * F((r + l) / 2)); } double asr( double l,//区间左边界 double r,//区间右边界 double integral,//该区间的辛普森积分 double esp ) { double mid = (l + r) / 2; double in_l = simpson(l, mid), in_r = simpson(mid, r); if (fabs(in_l + in_r - integral) > esp * 15) //细分有价值 return asr(l, mid, in_l, esp) + asr(mid, r, in_r, esp); else return in_l + in_r + (in_l + in_r - integral) / 15.0;//返回这个肯定比返回integral精度更高 } int main() { cout << setprecision(16)<<"估算" << asr(1, 8, simpson(1, 8), 1e-7) << " && 精确" << PF(8) - PF(1) << endl; cout << "计算次数:" << count_simpson << endl; return 0; }
运行结果：
扩展
为什么我非要用辛普森，这个算法为什么不能用梯形法则代替辛普森的作用？其实是可以用梯形法则代替辛普森的。
但是无论是计算量还是精度来说效果都不是很好（QAQ）。不用更高阶的原因也很简单，提高阶增加编码难度同时提高的精度难以弥补耗时。
后记
高考和强基计划审核结束，笔者如愿以偿地被理想的大学录取，由于录取专业与数学强相关，日后更新的文件也将高度围绕数学方面展开。这个排版调了我半天，emm，以后还是老老实实用markdown吧。
__EOF__
