「学习笔记」线段树优化建图

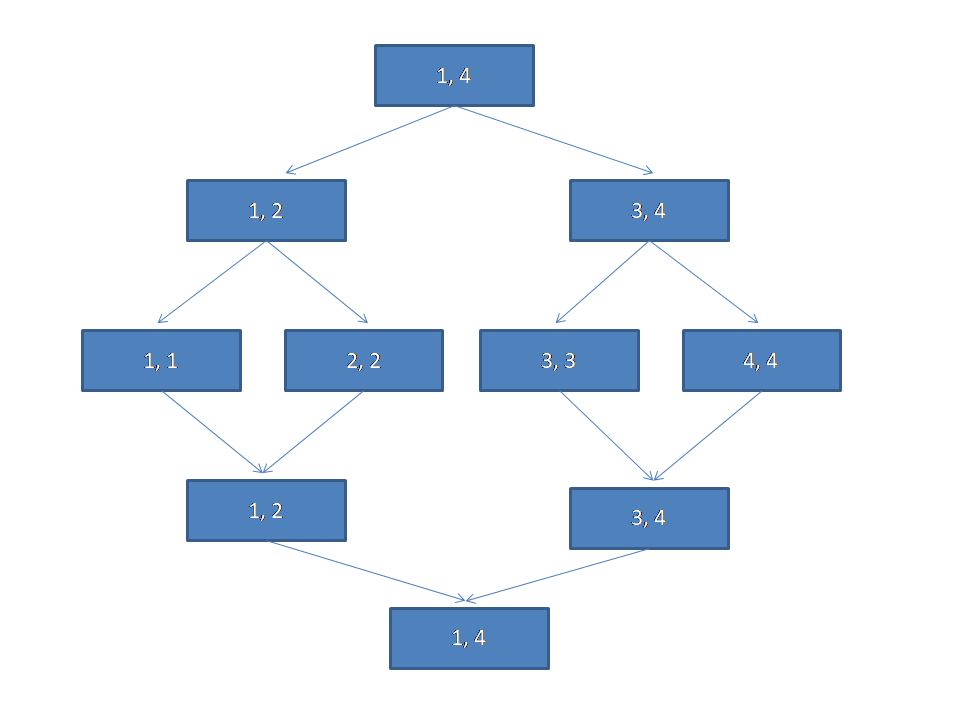
在建图连边的过程中，我们时常会碰到这种题目，一个点向一段连续的区间中的点连边或者一个连续的区间向一个点连边，如果我们真的一条一条连过去，那一旦点的数量多了复杂度就爆炸了，这里就需要用线段树的区间性质来优化我们的建图了。

那棵线段树大概长这个样子。

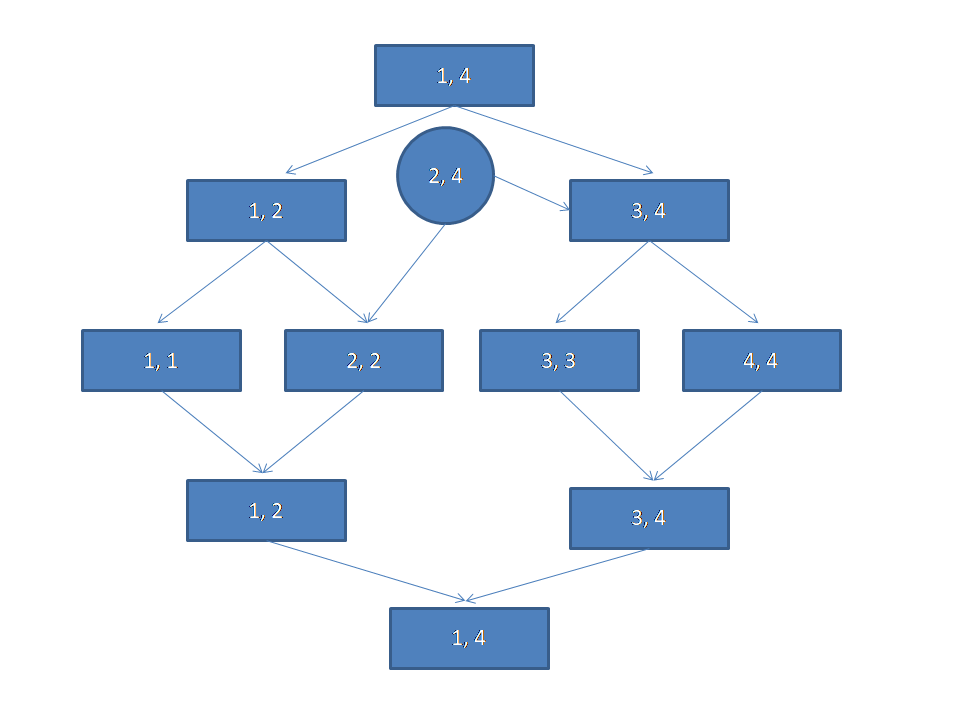
到时候加边的时候是这个样子的。（为了不影响边的显示，只能把点放在这里了）

个人感觉，这是一个可以优化的方法，算不上什么很高级的算法或数据结构，题目照常做即可。

题目#

Legacy - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

模板题，也是自己少数不看题解独立做出来的题目。

线段树上建图 + 最短路。

这里还用了动态开点（因为这个蒟蒻不会用二叉树的性质来建造下面部分的线段树）。

//The code was written by yifan, and yifan is neutral!!!

#include 
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

using pil = pair<int, ll>;
using pli = pair<ll, int>;

const int N = 1e5 + 5;

int n, q, s, tot, rt1, rt2;
int pos[N];
ll dis[N << 3];
vector<pil> e[N << 3];
bitset<(N << 3)> vis;

struct seg {
    int l, r, lson, rson;
} t[N << 3];

inline int ls(int u) {
    return t[u].lson;
}

inline int rs(int u) {
    return t[u].rson;
}

void build(int &u, int l, int r) {
    u = ++ tot;
    t[u] = seg{l, r};
    if (l == r) {
        pos[l] = u;
        return ;
    }
    int mid = (l + r) >> 1;
    build(t[u].lson, l, mid);
    build(t[u].rson, mid + 1, r);
    e[u].emplace_back(ls(u), 0);
    e[u].emplace_back(rs(u), 0);
}

void add1(int u, int lr, int rr, int v, ll w) {
    if (lr <= t[u].l && t[u].r <= rr) {
        e[v].emplace_back(u, w);
        return ;
    }
    int mid = (t[u].l + t[u].r) >> 1;
    if (lr <= mid) {
        add1(ls(u), lr, rr, v, w);
    }
    if (rr > mid) {
        add1(rs(u), lr, rr, v, w);
    }
}

void add2(int u, int lr, int rr, int v, ll w) {
    if (lr <= t[u].l && t[u].r <= rr) {
        e[u].emplace_back(v, w);
        return ;
    }
    int mid = (t[u].l + t[u].r) >> 1;
    if (lr <= mid) {
        add2(ls(u), lr, rr, v, w);
    }
    if (rr > mid) {
        add2(rs(u), lr, rr, v, w);
    }
}

void dij(int S) {
    priority_queue<pli, vector<pli>, greater<pli> > q;
    int tot = (n << 2);
    for (int i = 1; i <= tot; ++ i) {
        dis[i] = 1e18;
    }
    dis[S] = 0;
    q.emplace(dis[S], S);
    while (! q.empty()) {
        pli fr = q.top();
        q.pop();
        int u = fr.second;
        if (vis[u]) continue ;
        for (pil it : e[u]) {
            int v = it.first;
            ll w = it.second;
            if (dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.emplace(dis[v], v);
            }
        }
    }
}

void build2(int &u, int l, int r) {
    if (l == r) {
        u = pos[l];
        return ;
    }
    u = ++ tot;
    t[u] = seg{l, r};
    int mid = (l + r) >> 1;
    build2(t[u].lson, l, mid);
    build2(t[u].rson, mid + 1, r);
    e[ls(u)].emplace_back(u, 0);
    e[rs(u)].emplace_back(u, 0);
}

int main() {
    n = read<int>(), q = read<int>(), s = read<int>();
    build(rt1, 1, n);
    build2(rt2, 1, n);
    for (int i = 1, op, u; i <= q; ++ i) {
        op = read<int>(), u = read<int>();
        if (op == 1) {
            int v = read<int>();
            ll w = read<ll>();
            e[pos[u]].emplace_back(pos[v], w);
        } else if (op == 2) {
            int l = read<int>(), r = read<int>();
            ll w = read<ll>();
            add1(rt1, l, r, pos[u], w);
        } else {
            int l = read<int>(), r = read<int>();
            ll w = read<ll>();
            add2(rt2, l, r, pos[u], w);
        }
    }
    dij(pos[s]);
    for (int i = 1; i <= n; ++ i) {
        if (dis[pos[i]] == 1e18) {
            cout << -1;
        } else {
            cout << dis[pos[i]];
        }
        putchar(' ');
    }
    putchar('\n');
    return 0;
}

P5025 [SNOI2017] 炸弹 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这是一道融合了线段树优化建图和 tarjan 缩点的题目，建好图后进行缩点，然后再 dfs 寻找能引爆的最左端点和最右端点。

//The code was written by yifan, and yifan is neutral!!!

#include 
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");

template<typename T>
inline T read() {
    T x = 0;
    bool fg = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        fg |= (ch == '-');
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    return fg ? ~x + 1 : x;
}

const int N = 5e5 + 5;
const int mod = 1e9 + 7;

int n, tim, Scc, mx;
int pos[N], dfn[N << 2], low[N << 2], scc[N << 2];
int le[N << 2], re[N << 2];
ll x[N], r[N];
vector<int> e[N << 2], st, ne[N << 2];
bitset<(N << 2)> vis;

struct seg {
    int l, r;
} t[N << 2];

inline int ls(int u) {
    return (u << 1);
}

inline int rs(int u) {
    return (u << 1 | 1);
}

void build(int u, int l, int r) {
    t[u] = seg{l, r};
    mx = max(mx, u);
    if (l == r) {
        pos[l] = u;
        return ;
    }
    int mid = (l + r) >> 1;
    build(ls(u), l, mid);
    build(rs(u), mid + 1, r);
    e[u].emplace_back(ls(u));
    e[u].emplace_back(rs(u));
}

void connect(int u, int l, int r, int lr, int rr, int v) {
    if (lr <= l && r <= rr) {
        if (v == u) return ;
        e[v].emplace_back(u);
        return ;
    }
    int mid = (l + r) >> 1;
    if (lr <= mid) {
        connect(ls(u), l, mid, lr, rr, v);
    }
    if (rr > mid) {
        connect(rs(u), mid + 1, r, lr, rr, v);
    }
}

void tarjan(int u) {
    dfn[u] = low[u] = ++ tim;
    st.emplace_back(u);
    for (int v : e[u]) {
        if (! dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (! scc[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (dfn[u] == low[u]) {
        scc[u] = ++ Scc;
        le[Scc] = min(t[u].l, le[Scc]);
        re[Scc] = max(t[u].r, re[Scc]);
        while (st.back() != u) {
            scc[st.back()] = Scc;
            le[Scc] = min(t[st.back()].l, le[Scc]);
            re[Scc] = max(t[st.back()].r, re[Scc]);
            st.pop_back();
        }
        st.pop_back();
    }
}

void dfs(int u) {
    vis.set(u);
    for (int v : ne[u]) {
        if (vis[v]) {
            le[u] = min(le[u], le[v]);
            re[u] = max(re[u], re[v]);
            continue ;
        }
        dfs(v);
        le[u] = min(le[u], le[v]);
        re[u] = max(re[u], re[v]);
    }
}

int main() {
    n = read<int>();
    for (int i = 1; i <= n; ++ i) {
        x[i] = read<ll>(), r[i] = read<ll>();
    }
    memset(le, 127, sizeof le);
    build(1, 1, n);
    for (int i = 1, L, R; i <= n; ++ i) {
        if (!r[i])  continue ;
        L = lower_bound(x + 1, x + n + 1, x[i] - r[i]) - x;
        R = upper_bound(x + 1, x + n + 1, x[i] + r[i]) - x - 1;
        connect(1, 1, n, L, R, pos[i]);
        t[pos[i]] = seg{L, R};
    }
    for (int i = 1; i <= n; ++ i) {
        if (! dfn[i]) {
            tarjan(i);
        }
    }
    for (int i = 1; i <= mx; ++ i) {
        for (int u : e[i]) {
            if (scc[u] == scc[i])   continue ;
            ne[scc[i]].emplace_back(scc[u]);
        }
    }
    for (int i = 1; i <= Scc; ++ i) {
        sort(ne[i].begin(), ne[i].end());
        ne[i].erase(unique(ne[i].begin(), ne[i].end()), ne[i].end());
    }
    for (int i = 1; i <= Scc; ++ i) {
        if (! vis[i]) {
            dfs(i);
        }
    }
    ll ans = 0;
    for (int i = 1; i <= n; ++ i) {
        ans = (ans + (1ll * (1ll * re[scc[pos[i]]] - le[scc[pos[i]]] + 1) * i) % mod) % mod;
    }
    cout << ans;
    putchar('\n');
    return 0;
}