• 【数据结构】排序

    目录

    1.概念

    2.常见排序算法的实现

    2.1插入排序

    2.2希尔排序

    2.3选择排序

    2.4堆排序

    2.5冒泡排序

    2.5快速排序

    2.5.1Hoare法

    2.5.2挖坑法

    2.5.3前后指针法

    2.5.4三数取中法

    2.5.5非递归实现快排

    2.6归并排序

    2.6.1递归实现 

    2.6.2非递归实现

    2.7海量数据排序问题

    3.其他非基于比较排序

    3.1计数排序

    3.2基数排序

    3.3桶排序

    4.总结

    1.概念

    所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作

    内部排序：数据元素全部放在内存中的排序.
    外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序.

    稳定性：排完序后相同元素是否是原有顺序。

    例如：对 3   5   6    2   7   5 排序：

              稳定：    2    3    5    5    6    7

              不稳定：2    3    5    5    6    7

    注意：一个本身就稳定的排序，可以实现为不稳定排序；

               一个本身就不稳定的排序，不可能实现为稳定排序.


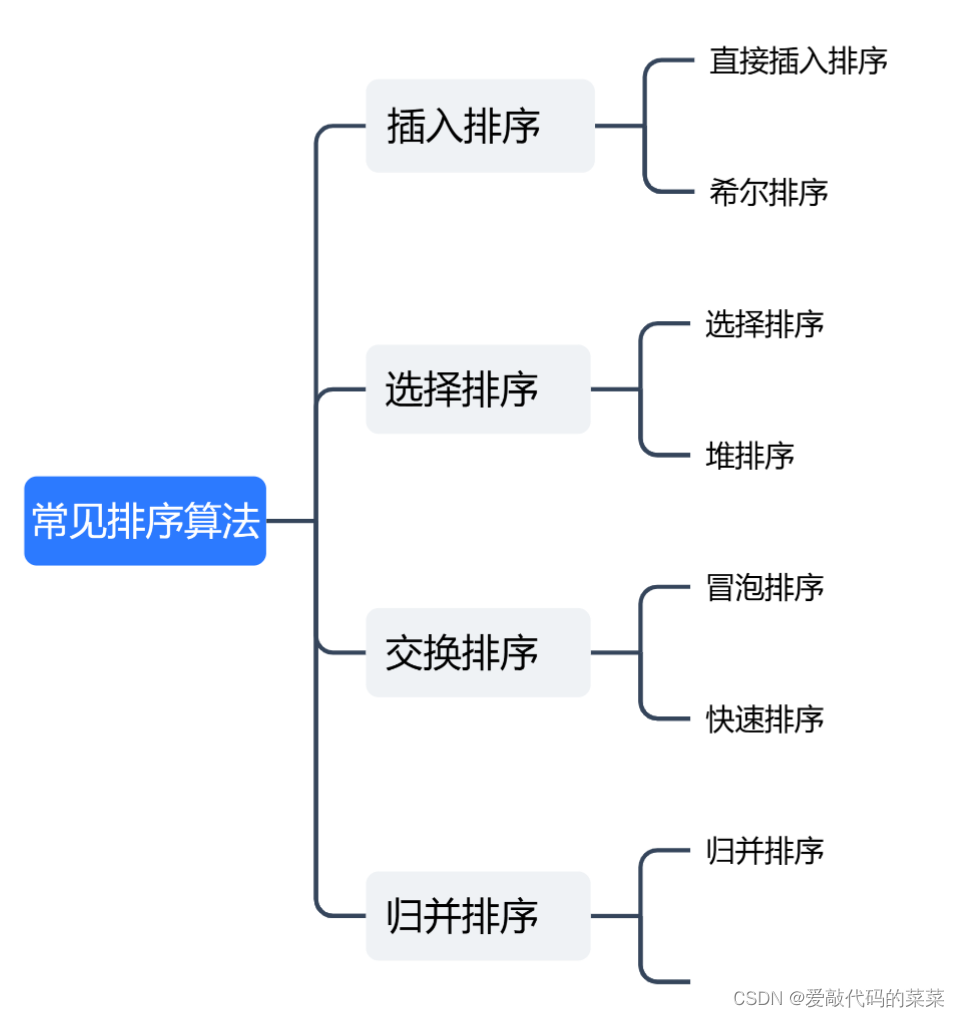
    2.常见排序算法的实现

    2.1插入排序

    时间复杂度：O(N^2)
    空间复杂度：O(1)
    稳定性：稳定排序

    1. public static void insertSort(int[] array) {
    2.  
    3.     for (int i = 1; i < array.length; i++) {
    4.         int tmp = array[i];
    5.         int j = i - 1; //每一次循环j都指向i的前一个
    6.         for (; j >= 0 ; j--) {
    7.             if (array[j] > tmp) { //这里如果时array[j] >= tmp，就不是稳定排序
    8.                 array[j+1] = array[j]; //也就是i和j交换
    9.             }
    10.             else {
    11.                 break;
    12.             }
    13.         }
    14.         array[j+1] = tmp;
    15.     }
    16. }

    2.2希尔排序

    步骤：分组（缩小增量），组内进行插入排序

    时间复杂度：不确定
    空间复杂度：O(1)
    稳定性：不稳定排序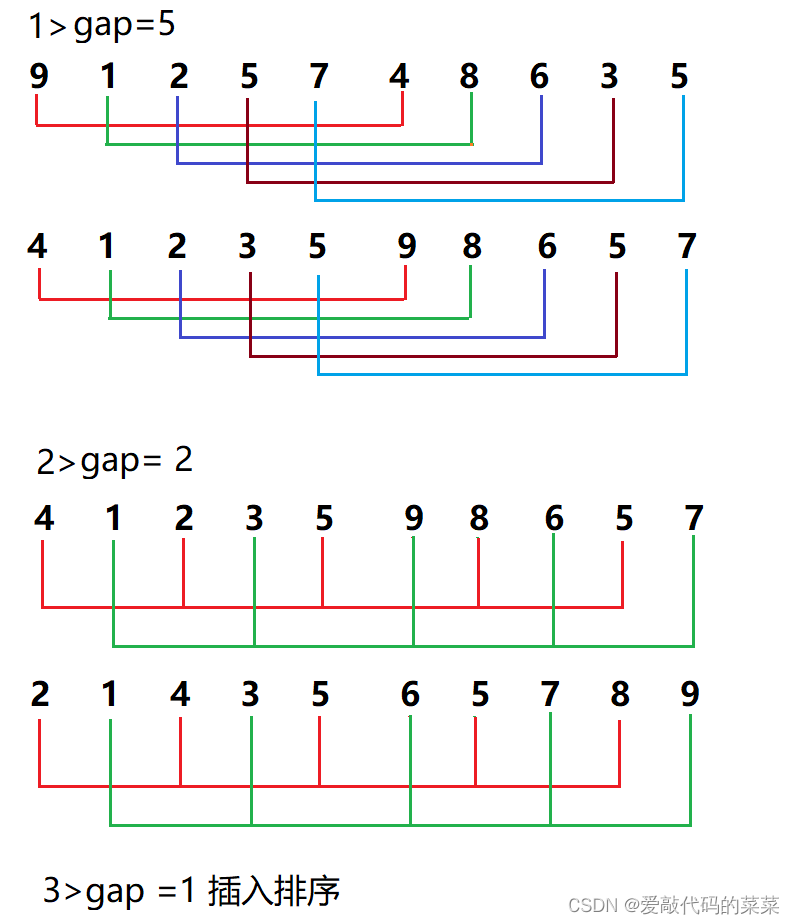

    1. public static void shell(int[] array,int gap) { //和插入排序十分相似
    2.                                                 //区别在于所有1改为了gap
    3.     for (int i = gap; i < array.length; i++) { // 注意是i++不是i+gap,交替排序每个组
    4.         int tmp = array[i];
    5.         int j = i - gap;
    6.         for (; j >= 0 ; j -= gap) {
    7.             if (array[j] > tmp) {
    8.                 array[j+gap] = array[j];
    9.             }
    10.             else {
    11.                 break;
    12.             }
    13.         }
    14.         array[j+gap] = tmp;
    15.     }
    16. }
    17.  
    18. public static void shellSort(int[] array) {
    19.     int gap = array.length;
    20.     while (gap > 1) {
    21.         gap /= 2;
    22.         shell(array,gap);
    23.     }
    24. }

    2.3选择排序

    步骤：一个一个排序，每次循环找到剩余元素中的最小元素放在前面。

    时间复杂度：O(N^2)
    空间复杂度：O(1)
    稳定性：不稳定排序

    1. public static void selectSort(int[] array) {
    2.     for (int i = 0; i < array.length; i++) {
    3.         int minIndex = array[i];
    4.         for (int j = i+1; j < array.length; j++) {
    5.             if (array[j] < minIndex) {
    6.                 int tmp = minIndex;
    7.                 minIndex = array[j];
    8.                 array[j] = tmp;
    9.             }
    10.         }
    11.         array[i] = minIndex;
    12.     }
    13. }

    2.4堆排序

    时间复杂度：O(n*logn) 对数据不敏感，不管有序无序都是这个表达式.
    空间复杂度：O(1)
    稳定性：不稳定排序

    1. private static void swap(int[] array,int i,int j) {
    2.     int tmp = array[i];
    3.     array[i] = array[j];
    4.     array[j] = tmp;
    5. }
    6.  
    7. public static void heapSort(int[] array) {
    8.     createBigHeap(array); //创建一个大根堆
    9.     int end = array.length-1;
    10.     while (end > 0) {
    11.         swap(array,end,0);
    12.         siftDown(array,0,end);
    13.         end--;
    14.     }
    15. }
    16.  
    17. private static void createBigHeap(int[] array) {
    18.     for (int i = (array.length-1-1) / 2; i >= 0 ; i--) {
    19.         siftDown(array,i,array.length);
    20.     }
    21. }
    22.  
    23. private static void siftDown(int[] array,int parent,int len) {
    24.     int child = 2*parent+1;
    25.     while (child < len) {
    26.         if(child+1 < len && array[child] < array[child+1]) {
    27.             child++;
    28.         }
    29.         if(array[child] > array[parent]) {
    30.             swap(array,child,parent);
    31.             parent = child;
    32.             child = 2*parent+1;
    33.         }else {
    34.             break;
    35.         }
    36.     }
    37. }

    2.5冒泡排序

    时间复杂度：O(N^2) 对数据不敏感，不管有序无序都是这个表达式
    空间复杂度：O(1)
    稳定性：稳定排序

    1. private static void swap(int[] array,int i,int j) {
    2.     int tmp = array[i];
    3.     array[i] = array[j];
    4.     array[j] = tmp;
    5. }
    6.  
    7. public static void bubbleSort(int[] array) {
    8.  
    9.     for (int i = 0; i < array.length-1; i++) {
    10.         boolean flg = false;
    11.         for (int j = 0; j < array.length-1-i; j++) {
    12.             if(array[j] > array[j+1]) {
    13.                 swap(array,j,j+1);
    14.                 flg = true;
    15.             }
    16.         }
    17.         if(!flg) { //当flag为假时break
    18.             break;
    19.         }
    20.     }
    21. }

    2.5快速排序

    基于分治法（分而治之）的一个排序算法。

    时间复杂度：最好情况：O(n*logn)(记)，最坏情况：O(n^2)

    空间复杂度：最好情况：O(logn)(记)，最坏情况：O(n)

    稳定性：不稳定排序

    2.5.1Hoare法

    1. private static void swap(int[] array,int i,int j) {
    2.     int tmp = array[i];
    3.     array[i] = array[j];
    4.     array[j] = tmp;
    5. }
    6.  
    7. private static int partition(int[] array,int left,int right) {
    8.     int i = left;
    9.     int tmp = array[left];
    10.     while (left < right) {
    11.         //找到右边小于tmp的值
    12.         while (left < right && array[right] >= tmp) {
    13.             right--;
    14.         }
    15.         //找到左边小于tmp的值
    16.         while (left < right && array[left] <= tmp) {
    17.             left++;
    18.         }
    19.         //交换这两个值
    20.         swap(array,left,right);
    21.     }
    22.     swap(array,left,i);//交换中值和第一个值
    23.     return left;//返回中值
    24. }
    25.  
    26. private static void quick(int[] array,int start,int end) {
    27.     if (start >= end) {
    28.         return;
    29.     }
    30.     int pivot = partition(array,start,end);//找到中值
    31.  
    32.     quick(array,start,pivot-1);//递归左边
    33.     quick(array,pivot+1,end);//递归右边
    34. }
    35.  
    36. public static void quickSort(int[] array) {
    37.     quick(array,0,array.length-1);
    38. }

    2.5.2挖坑法

    类似于Hoare法，不过Hoare法是左右开弓双管齐下，挖坑法是左右分别来

    1. private static void swap(int[] array,int i,int j) {
    2.     int tmp = array[i];
    3.     array[i] = array[j];
    4.     array[j] = tmp;
    5. }
    6.  
    7. private static int partition(int[] array,int left,int right) {
    8.     int tmp = array[left];
    9.     while (left < right) {
    10.         while (left < right && array[right] >= tmp) {
    11.             right--;
    12.         }
    13.         array[left] = array[right];
    14.  
    15.         while (left < right && array[left] <= tmp) {
    16.             left++;
    17.         }
    18.         array[right] = array[left];
    19.     }
    20.     array[left] = tmp;
    21.     return left;
    22. }

    2.5.3前后指针法

    有点难以理解，不经常用。这里只是把大于中值和小于中值的数分别放到两边，不是完整的代码。

    1. private static int partition1(int[] array, int left, int right) {
    2.     int prev = left ;//后指针
    3.     int cur = left+1;//前指针
    4.     while (cur <= right) {
    5.         if(array[cur] < array[left] && array[++prev] != array[cur]) {
    6.             swap(array,cur,prev);
    7.         }
    8.         cur++;
    9.     }
    10.     swap(array,prev,left);
    11.     return prev;
    12. }

    2.5.4三数取中法

    这里也只是把大于中值和小于中值的数分别放到两边，不是完整的代码。

    1. private static int threeNum(int[] array,int left,int right) {
    2.  
    3.         int mid = (left+right) / 2;
    4.         if(array[left] < array[right]) {
    5.             if(array[mid] < array[left]) {
    6.                 return left;
    7.             }else if(array[mid] > array[right]) {
    8.                 return right;
    9.             }else {
    10.                 return mid;
    11.             }
    12.         }else {
    13.             if(array[mid] < array[right]) {
    14.                 return right;
    15.             }else if(array[mid] > array[left]) {
    16.                 return left;
    17.             }else {
    18.                 return mid;
    19.             }
    20.         }
    21.     }

    2.5.5非递归实现快排

    只是模拟递归实现，所以时间复杂度并没有本质的变化，但是非递归可以减少栈空间的开销。栈和队列都可以实现。

    1. public static void quickSort(int[] array) {
    2.  
    3.         Stack stack = new Stack<>();//非递归使用栈
    4.         int start = 0;
    5.         int end = array.length-1;
    6.  
    7.         if(end - start +1 <= 20) {
    8.             //数据太少直接插入排序
    9.             insertSort(array,start,end);
    10.             return;
    11.         }
    12.  
    13.         //三数取中
    14.         int mid = threeNum(array,start,end);
    15.         //交换
    16.         swap(array,mid,start);
    17.  
    18.         int pivot = partition(array,start,end);
    19.  
    20.         if(pivot > start+1) { //pivot左边至少有两个元素
    21.             stack.push(start);
    22.             stack.push(pivot-1);
    23.         }
    24.         if(pivot < end-1) { //pivot右边至少有两个元素
    25.             stack.push(pivot+1);
    26.             stack.push(end);
    27.         }
    28.  
    29.         while (!stack.empty()) {
    30.             end = stack.pop(); //注意先弹给end
    31.             start = stack.pop();
    32.  
    33.             if(end - start +1 <= 20) {
    34.                 //直接插入排序
    35.                 insertSort(array,start,end);
    36.             }else {
    37.                 //三数取中
    38.                 mid = threeNum(array,start,end);
    39.                 //交换
    40.                 swap(array,mid,start);
    41.  
    42.                 pivot = partition(array, start, end);
    43.                 if (pivot > start + 1) {
    44.                     stack.push(start);
    45.                     stack.push(pivot - 1);
    46.                 }
    47.                 if (pivot < end - 1) {
    48.                     stack.push(pivot + 1);
    49.                     stack.push(end);
    50.                 }
    51.             }
    52.         }
    53.     }

    2.6归并排序

    步骤：分解+合并

    时间复杂度：O(n logn)

    空间复杂度：O(n)

    稳定性：稳定排序

    2.6.1递归实现 

    1. private static void merge(int[] array,int left,int mid,int right) {
    2.  
    3.     int s1 = left;
    4.     int e1 = mid;
    5.     int s2 = mid+1;
    6.     int e2 = right;
    7.  
    8.     int[] tmpArr = new int[right-left+1];//申请一个数组用来存合并后的数据
    9.     int k = 0;//tmpArr数组的下标
    10.  
    11.     while (s1 <= e1 && s2 <= e2) { //说明左右树都有数据
    12.  
    13.         if(array[s1] <= array[s2]){ //哪个小先放哪个
    14.             tmpArr[k++] = array[s1++];
    15.         }else {
    16.             tmpArr[k++] = array[s2++];
    17.         }
    18.     }
    19.  
    20.     //走到这说明某一边走完了，将剩下一边全部放入tmpArr中
    21.     while (s1 <= e1) {
    22.         tmpArr[k++] = array[s1++];
    23.     }
    24.     while (s2 <= e2) {
    25.         tmpArr[k++] = array[s2++];
    26.     }
    27.     
    28.     //将tmpArr数组再拷入原数组中
    29.     for (int i = 0; i < k; i++) {
    30.         array[i+left] = tmpArr[i];
    31.     }
    32. }
    33.  
    34. private static void mergeSortFunc(int[] array,int left,int right) {
    35.     if(left >= right) {
    36.         return;
    37.     }
    38.     int mid = (left+right) / 2;
    39.     
    40.     //分解
    41.     mergeSortFunc(array,left,mid);//递归左边
    42.     mergeSortFunc(array,mid+1,right);//递归右边
    43.  
    44.     merge(array,left,mid,right);//合并
    45. }
    46.  
    47. public static void mergeSort(int[] array) {
    48.     mergeSortFunc(array,0,array.length-1);
    49. }

    2.6.2非递归实现

    1. public static void mergeSort1(int[] array) {
    2.     int gap = 1;
    3.     while (gap < array.length) {
    4.         for (int i = 0; i < array.length; i = i + gap*2) {
    5.             int left = i;
    6.             int mid = left+gap-1;
    7.             int right = mid+gap;
    8.  
    9.             //mid和right有可能会越界
    10.             if(mid >= array.length) {
    11.                 mid = array.length-1;
    12.             }
    13.             if(right >= array.length) {
    14.                 right = array.length-1;
    15.             }
    16.  
    17.             merge(array,left,mid,right);//合并
    18.         }
    19.         gap *= 2;
    20.     }
    21. }

    2.7海量数据排序问题

    前提：内存只有1G，而需要排序的内容有100G，此时需要再磁盘等外部存储进行排序。

    归并排序是最常见的外部排序。

    步骤：1> 先把文件切分成 200 份，每份512M；

               2>分别对每份512M排序；

               3> 进行二路归并，再对 200 份有序文件做归并过程。

    3.其他非基于比较排序

    3.1计数排序

    适用于比较集中的数据，空间换时间。

    时间复杂度：O(范围+n)，范围越小，复杂度越小。

    空间复杂度：O(范围)

    稳定性：稳定排序

    1. public static void countArray(int[] array) {
    2.  
    3.     //找到数组中的最大值和最小值
    4.     int maxVal = array[0];
    5.     int minVal = array[0];
    6.     for (int i = 1; i < array.length; i++) {
    7.         if (array[i] > maxVal) {
    8.             maxVal = array[i];
    9.         }
    10.         if (array[i] < minVal) {
    11.             minVal = array[i];
    12.         }
    13.     }
    14.  
    15.     //将array中每个元素的个数存入计数数组count中
    16.     int range = maxVal - minVal + 1; //确定计数数组大小
    17.     int[] count = new int[range];
    18.     for (int i = 0; i < array.length; i++) {
    19.         int val = array[i];
    20.         count[val-minVal]++;
    21.     }
    22.  
    23.     //遍历计数数组，打印排完序的结果
    24.     int index = 0; //原数组的下标
    25.     for (int i = 0; i < count.length; i++) {
    26.         int val = count[i];
    27.         while (val-- != 0) { //val为0不进入循环
    28.             array[index] = i + minVal;//覆盖原数组
    29.             index++;
    30.         }
    31.     }
    32. }

    3.2基数排序

    基数排序

    3.3桶排序

    桶排序

    类似于基数排序，只不过是在桶里直接进行排序。

    4.总结

    排序时间复杂度空间复杂度稳定性
    插入n^21√
    希尔n^1.3~n^1.51×
    选择n^21×
    堆nlogn1×
    冒泡n^21√
    快速nlogn / n^2logn / n×
    归并nlognn√
    计数范围+n范围√

    这篇博客真的是知识量巨大啊(​​​​​

  • 相关阅读:
    MVC第三波书店图书类型获取和实现下拉框功能
    06条件判断
    WPF利用Path自定义画头部导航条(TOP)样式
    用Hopper修改代理软件端口
    计算机是怎么跑起来的？从零开始手动组装微型计算机
    Innodb是如何运转的
    Linux常用命令——bmodinfo命令
    我打赌你以前从未使用过TypeScript的断言函数（译）
    大佬指明方向！使用微服务的最佳实践以及如何避免采用微服务架构可能带来的复杂性陷阱
    Python可视化应用实战案例30篇（一）-基础绘图命令详解含大量示例代码（附Python代码）
  • 原文地址：https://blog.csdn.net/qq_74455045/article/details/131608810