-
红黑树及其应用介绍(万字长文)
红黑树
定义与性质
红黑树是一种特殊的二叉查找树,它遵循了特定的规则使得其具有了平衡性。红黑树的定义包括以下几个方面:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色的。
- 每个叶子节点(NIL节点,空节点)是黑色的。
- 对于任意一个节点,其子节点中黑色节点的数量不少于 1。
- 对于任意一个节点,从该节点到其叶子节点的所有路径上,黑色节点数量相同。
红黑树的性质:
- 红黑树是一棵二叉查找树。
- 红黑树的平衡是指,对于任意一个节点,其左右子树的高度差不超过 1。
- 红黑树的查找、插入、删除等操作的时间复杂度都可以做到 O(logn)。
- 红黑树的颜色变换规则使得它在插入、删除等操作后能够快速地恢复平衡。
红黑树在很多领域中都有广泛的应用,例如操作系统、数据库、图形学等。它的平衡性和高效的操作性能使得它成为一种非常优秀的数据结构,其结构图如下。
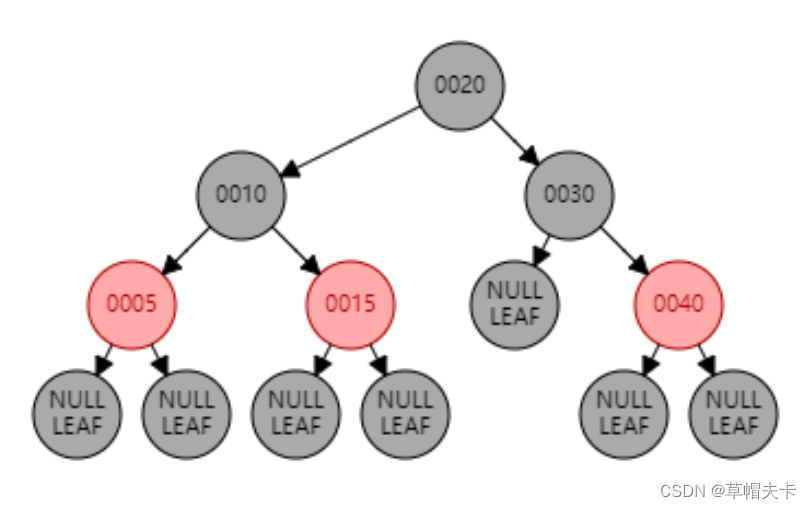
查找遍历
红黑树的查找遍历有以下几种常用的方法:
- 递归遍历:使用递归的方式遍历红黑树,对于每个节点,递归遍历其左子树和右子树。
- 前序遍历:先遍历根节点,然后按照前序遍历的方式遍历左子树,最后按照前序遍历的方式遍历右子树。
- 中序遍历:先遍历左子树,然后遍历根节点,最后按照中序遍历的方式遍历右子树。
- 后序遍历:先遍历左子树,然后按照后序遍历的方式遍历右子树,最后遍历根节点。
- 层序遍历:按照层级的方式遍历红黑树,对于每一层,按照从左到右的顺序遍历该层的所有节点。
递归遍历
红黑树的递归遍历是指使用递归的方式遍历红黑树的所有节点。具体的遍历方式可以是前序遍历、中序遍历、后序遍历等。以下是一个使用递归实现红黑树前序遍历的 Java 代码示例:
public void preorderTraversal(TreeNode root) { if (root == null) { return; } System.out.print(root.val + " "); // 先输出根节点的值 preorderTraversal(root.left); // 递归遍历左子树 preorderTraversal(root.right); // 递归遍历右子树 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
其中,
TreeNode表示红黑树的节点,其代码如下:class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } }- 1
- 2
- 3
- 4
- 5
- 6
在递归遍历的过程中,需要注意以下几点:
- 对于每个节点,先递归遍历其左子树,再递归遍历其右子树。
- 对于叶子节点(
left和right都为null),不需要进行递归遍历。 - 递归终止条件为节点为
null。
前中后序遍历
红黑树的前序遍历、中序遍历和后序遍历是指按照不同的顺序遍历红黑树的节点。
前序遍历:先访问根节点,然后按照前序遍历的方式遍历左子树,最后按照前序遍历的方式遍历右子树。
中序遍历:先按照中序遍历的方式遍历左子树,然后访问根节点,最后按照中序遍历的方式遍历右子树。
后序遍历:先按照后序遍历的方式遍历左子树,然后按照后序遍历的方式遍历右子树,最后访问根节点。
以下是一个使用递归实现红黑树前序遍历、中序遍历和后序遍历的 Java 代码示例:
import java.util.ArrayList; import java.util.List; class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } /** * 前序遍历 */ public List<Integer> preorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); preorderTraversal(root, result); return result; } private void preorderTraversal(TreeNode root, List<Integer> result) { if (root == null) { return; } result.add(root.val); // 先访问根节点 preorderTraversal(root.left, result); // 递归遍历左子树 preorderTraversal(root.right, result); // 递归遍历右子树 } /** * 中序遍历 */ public List<Integer> inorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); inorderTraversal(root, result); return result; } private void inorderTraversal(TreeNode root, List<Integer> result) { if (root == null) { return; } inorderTraversal(root.left, result); result.add(root.val); inorderTraversal(root.right, result); } /** * 后序遍历 */ public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); postorderTraversal(root, result); return result; } private void postorderTraversal(TreeNode root, List<Integer> result) { if (root == null) { return; } postorderTraversal(root.left, result); postorderTraversal(root.right, result); result.add(root.val); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
层序遍历
红黑树的层序遍历是指按照从根节点到叶子节点的顺序,依次访问每个节点。具体来说,遍历顺序为从根节点开始,按照深度优先搜索的方式遍历每个节点,对于每个节点,先访问其左子树,再访问其右子树。
在 Java 中,可以使用递归或者迭代的方式实现红黑树的层序遍历。
递归实现:
import java.util.ArrayList; import java.util.List; import java.util.Optional; public class RedBlackTree { private final TreeNode root; public RedBlackTree(TreeNode root) { this.root = root; } public List<Integer> levelOrderTraversal() { List<Integer> result = new ArrayList<>(); levelOrderTraversal(root, 0, result); return result; } private void levelOrderTraversal(TreeNode node, int level, List<Integer> result) { if (node == null) { return; } if (result.size() == level) { result.add(node.val); } else { result.set(level, node.val); } levelOrderTraversal(node.left, level + 1, result); levelOrderTraversal(node.right, level + 1, result); } } class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
迭代实现:
import java.util.ArrayList; import java.util.List; import java.util.Stack; public class RedBlackTree { private final TreeNode root; public RedBlackTree(TreeNode root) { this.root = root; } public List<Integer> levelOrderTraversal() { List<Integer> result = new ArrayList<>(); Stack<TreeNode> stack = new Stack<>(); TreeNode current = root; while (current != null || !stack.isEmpty()) { while (current != null) { result.add(current.val); stack.push(current); current = current.left; } current = stack.peek(); current = current.right; stack.pop(); } return result; } } class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
插入与删除
红黑树是一种特殊的二叉查找树,它遵循了特定的规则使得其具有了平衡性,因此查询、插入和删除操作的时间复杂度都能够保持在对数级别。
红黑树的插入操作如下:
- 如果插入的节点的父节点是黑色的,则直接将该节点插入到树中。
- 如果插入的节点的父节点是红色的,则需要进行变色操作。具体来说,如果该节点的祖父节点是黑色的,则将该节点的父节点和祖父节点都变成黑色的。如果该节点的祖父节点是红色的,则需要进行旋转操作,将该节点的父节点和祖父节点的颜色进行交换,并且可能需要继续旋转,直到该节点的祖父节点是黑色的为止。
红黑树的删除操作如下:
- 如果要删除的节点没有子节点,则直接将该节点删除,并且将其父节点变成黑色的。
- 如果要删除的节点只有一个子节点,则将该节点的子节点替代该节点的位置,并且将该节点的父节点和子节点都变成黑色的。
- 如果要删除的节点有两个子节点,则需要找到该节点的后继节点,也就是左子树的最大值节点。然后将该节点的后继节点替代该节点的位置,并且将该节点的父节点和后继节点都变成黑色的。如果该节点的后继节点的父节点是红色的,则需要进行变色操作。
在进行变色操作时,需要遵循以下规则:
- 每个节点都必须是红色或者黑色。
- 根节点是黑色的。
- 如果一个节点是红色的,那么它的子节点必须是黑色的(也就是说不存在连续的红色节点)。
- 对于任意一个节点,从该节点到其叶子节点的所有路径上,黑色节点数量相同。
这些规则保证了红黑树的平衡性,使得查询、插入和删除操作的时间复杂度都能够保持在对数级别。
插入
红黑树插入节点的代码实现可以分为以下几个步骤:
- 新建一个节点,并将新节点的值设置为待插入的值。
- 按照红黑树的性质,将新节点插入到合适的位置。
- 如果新节点是红色,需要进行旋转操作来保持红黑树的性质。
- 更新父节点的指针,使其指向新节点。
- 如果根节点为空,将新节点设置为根节点。
以下是红黑树插入节点的详细代码实现:
public class RedBlackTree<Key extends Comparable<Key>, Value> { private static final boolean RED = true; private static final boolean BLACK = false; private Node root; private class Node { Key key; Value value; Node left, right; int size; boolean color; Node(Key key, Value value, int size, boolean color) { this.key = key; this.value = value; this.size = size; this.color = color; } } private boolean isRed(Node x) { if (x == null) { return false; } return x.color == RED; } private Node rotateLeft(Node h) { Node x = h.right; h.right = x.left; x.left = h; x.color = h.color; h.color = RED; x.size = h.size; h.size = size(h.left) + size(h.right) + 1; return x; } private Node rotateRight(Node h) { Node x = h.left; h.left = x.right; x.right = h; x.color = h.color; h.color = RED; x.size = h.size; h.size = size(h.left) + size(h.right) + 1; return x; } private void flipColors(Node h) { h.color = RED; h.left.color = BLACK; h.right.color = BLACK; } public int size() { return size(root); } private int size(Node x) { if (x == null) { return 0; } return x.size; } public void put(Key key, Value value) { root = put(root, key, value); root.color = BLACK; } private Node put(Node h, Key key, Value value) { if (h == null) { return new Node(key, value, 1, RED); } int cmp = key.compareTo(h.key); if (cmp < 0) { h.left = put(h.left, key, value); } else if (cmp > 0) { h.right = put(h.right, key, value); } else { h.value = value; } if (isRed(h.right) && !isRed(h.left)) { h = rotateLeft(h); } if (isRed(h.left) && isRed(h.left.left)) { h = rotateRight(h); } if (isRed(h.left) && isRed(h.right)) { flipColors(h); } h.size = size(h.left) + size(h.right) + 1; return h; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
以上代码实现了红黑树的插入操作。在实际应用中,我们可以根据需要选择合适的遍历方式来访问红黑树中的节点。
删除
红黑树删除节点的代码实现可以分为以下几个步骤:
- 找到待删除节点。
- 如果待删除节点是叶子节点(NIL节点),直接删除。
- 如果待删除节点只有一个子节点,用其子节点替换该节点。
- 如果待删除节点有两个子节点,找到其右子树中的最小节点(或左子树中的最大节点),用该节点替换待删除节点。
- 更新父节点的指针,使其指向待删除节点的子节点。
- 如果根节点为空,将待删除节点设置为根节点。
以下是红黑树删除节点的详细代码实现:
public class RedBlackTree<Key extends Comparable<Key>, Value> { private static final boolean RED = true; private static final boolean BLACK = false; private Node root; private class Node { Key key; Value value; Node left, right; int size; boolean color; Node(Key key, Value value, int size, boolean color) { this.key = key; this.value = value; this.size = size; this.color = color; } } private Node deleteMin(Node h) { if (h.left == null) { return null; } h.left = deleteMin(h.left); h.size = size(h.left) + size(h.right) + 1; return balance(h); } private Node deleteMax(Node h) { if (h.right == null) { return null; } h.right = deleteMax(h.right); h.size = size(h.left) + size(h.right) + 1; return balance(h); } private Node balance(Node h) { if (isRed(h.right)) { h = rotateLeft(h); } if (isRed(h.left) && isRed(h.left.left)) { h = rotateRight(h); } if (isRed(h.left) && isRed(h.right)) { flipColors(h); } return h; } private void flipColors(Node h) { h.color = RED; h.left.color = BLACK; h.right.color = BLACK; } public void delete(Key key) { root = delete(root, key); } private Node delete(Node h, Key key) { if (key.compareTo(h.key) < 0) { if (!isRed(h.left) && !isRed(h.left.left)) { h = moveRedLeft(h); } h.left = delete(h.left, key); } else { if (isRed(h.left)) { h = rotateRight(h); } if (key.compareTo(h.key) == 0 && (h.right == null)) { return null; } if (!isRed(h.right) && !isRed(h.right.left)) { h = moveRedRight(h); } if (key.compareTo(h.key) == 0) { Node x = min(h.right); h.key = x.key; h.value = x.value; h.right = deleteMin(h.right); } else { h.right = delete(h.right, key); } } return balance(h); } private Node min(Node x) { if (x.left == null) { return x; } else { return min(x.left); } } private Node max(Node x) { if (x.right == null) { return x; } else { return max(x.right); } } private Node moveRedLeft(Node h) { flipColors(h); if (isRed(h.right.left)) { h.right = rotateRight(h.right); h = rotateLeft(h); flipColors(h); } return h; } private Node moveRedRight(Node h) { flipColors(h); if (isRed(h.left.left)) { h = rotateRight(h); flipColors(h); } return h; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
复杂度分析
时间复杂度
红黑树的插入和删除操作的时间复杂度分析如下:
插入操作:
插入操作的时间复杂度主要取决于红黑树的高度。在最坏情况下,插入操作需要将新节点插入到树的最顶层,并且需要进行多次旋转操作来维护红黑树的性质。因此,插入操作的时间复杂度为 O(logn)。
删除操作:
删除操作的时间复杂度也主要取决于红黑树的高度。在最坏情况下,删除操作需要将被删除节点的父节点和祖先是红色节点,并且需要进行多次旋转操作来维护红黑树的性质。因此,删除操作的时间复杂度为 O(logn)。
总的来说,红黑树的插入和删除操作的时间复杂度都是 O(logn),这使得红黑树成为了一种非常高效的数据结构,适用于需要频繁进行插入和删除操作的场景。
空间复杂度
红黑树插入和删除操作的空间复杂度主要与树的高度相关。在最坏情况下,插入或删除操作可能需要进行多次旋转操作,导致树的高度增加。但是,由于红黑树的性质,树的高度始终不会超过 O(logn),因此插入和删除操作的空间复杂度均为 O(logn)。
在实际实现中,红黑树通常采用自平衡的方式来维护树的性质,避免了过多的旋转操作。这种实现方式的空间复杂度为 O(1)或 O(logn),具体取决于红黑树的具体实现方式。
总的来说,红黑树插入和删除操作的空间复杂度均为 O(logn)或 O(1),是一种非常高效的数据结构。
应用场景
Mysql 数据库索引
在 MySQL 数据库中,红黑树被广泛应用于 B+树索引结构中。
B+树索引是一种平衡的多路查找树,其结构与红黑树类似,具有以下优点:
-
快速查找:B+树索引能够快速地查找数据,因为它具有平衡的结构,可以将查找范围限制在最小的范围内。
-
高存储密度:B+树索引可以将大量数据存储在索引节点中,从而减少了存储空间的浪费。
-
支持范围查询:B+树索引可以支持范围查询,因为它具有顺序存储的特点,可以快速地定位到某个范围内的数据。
在 MySQL 数据库中,B+树索引通常存储在磁盘上,以提高查询效率。当数据量较大时,B+树索引可以显著提高数据库的查询速度。
具体来说,在 MySQL 数据库中,B+树索引是以文件的形式存储的,每个节点存储在一个磁盘块中。B+树索引的每个节点都包含了指向子节点的指针和指向数据记录的指针。在查询时,MySQL 数据库会根据 B+树索引的结构,快速地定位到所需的数据记录,从而提高查询效率。
红黑树在 B+树索引中的应用,使得 B+树索引具有了平衡的结构和快速的查找能力,从而提高了数据库的查询效率。
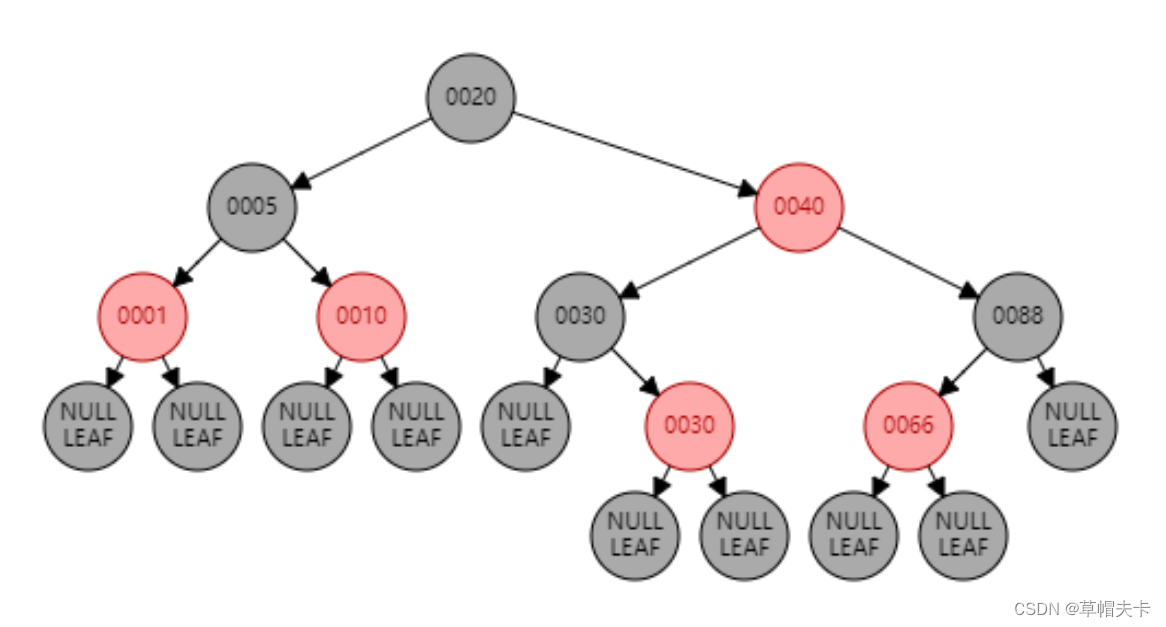
Java HashMap
Java HashMap 是一种常用的集合类,它是基于哈希表实现的。下面是 HashMap 的结构和工作原理的详细介绍:
Java 8 中 HashMap 的类定义
public class HashMap<K, V> extends AbstractMap<K, V> implements Map<K, V>, Cloneable, java.io.Serializable { // 省略了部分代码 }- 1
- 2
- 3
在这个类定义中,我们可以看到 HashMap 继承了
AbstractMap类,实现了Map接口,同时还实现了Cloneable和Serializable接口。这意味着 HashMap 是一个可克隆和可序列化的集合。在 HashMap 中,每个键值对都是一个
Entry对象,它存储在一个哈希桶中。哈希桶是一个数组,它的长度是 2 的幂次方,以提高哈希表的性能。- 数据结构:
HashMap 使用一个
Entry数组来存储数据,其中K是键类型,V是值类型。每个Entry对象包含一个键和一个值,它们通过哈希函数(通常是HashCode方法)关联起来。- 哈希函数:
HashMap 使用哈希函数将键转换为数组下标,以确定数据存储在数组中的位置。哈希函数的作用是将任意的键值转换为固定长度的、分散均匀的整数,从而减少冲突的可能性。HashMap 中使用的哈希函数是
HashCode方法,它是 Object 类的一个默认方法,每个类都可以重写它以生成自己的哈希值。- 冲突解决:
如果两个键通过哈希函数得到了相同的哈希值,就会发生冲突。HashMap 中解决冲突的方法是将冲突的键值存储在一个链表中,这个链表存储在哈希表的桶中。每个桶都包含一个头节点,指向链表中的第一个元素。当哈希冲突时,新元素将被添加到链表的末尾。
- 查找操作:
HashMap 的查找操作非常快速,它通过哈希函数将键转换为数组下标,然后在数组中查找与该键关联的值。如果找到了,就返回该值;如果没有找到,则返回
null。- 插入操作:
HashMap 的插入操作首先通过哈希函数将键转换为数组下标,然后在数组中查找与该键关联的值。如果找到了,就更新该值的值;如果没有找到,就创建一个新的
Entry对象,将其插入到数组的相应位置,并将其链接到哈希表的相应桶中的链表末尾。- 删除操作:
HashMap 的删除操作首先通过哈希函数将键转换为数组下标,然后在数组中查找与该键关联的值。如果找到了,就从链表中删除该值,并将该位置。
Java 8 中的 HashMap
Java 8 中的 HashMap 实现相比之前的版本做了一些改进和优化,主要包括以下几个方面:
-
初始容量:在 Java 8 中,HashMap 默认的初始容量是 16,而不是以前的 10。这是一个小的优化,可以减少哈希冲突的可能性,提高哈希表的性能。
-
负载因子:负载因子是哈希表中元素个数与哈希表大小的比值。在 Java 8 中,负载因子的默认值是 0.75,而不是以前的 0.75。这是一个较大的优化,可以减少哈希冲突的可能性,提高哈希表的性能。
-
红黑树:在 Java 8 中,当哈希表中的元素数量超过阈值(默认为 8)时,HashMap 会将哈希桶转换为红黑树。这是一个较大的优化,可以提高哈希表的查询性能,特别是在哈希冲突较多的情况下。
-
遍历器:在 Java 8 中,HashMap 提供了一个新的遍历器,称为
foreach遍历器,它可以方便地遍历哈希表中的元素。与以前的版本相比,它更加简洁和易于使用。
-
相关阅读:
理解RNN循环神经网络
java拼图游戏(待优化)
realman——基于SDK的pick_and_place
leetcode算法题--二叉树中和为某一值的路径
http客户端Feign
三十五、前端基础
工程管理系统简介 工程管理系统源码 java工程管理系统 工程管理系统功能设计
centos7安装cuda和nvidia-driver
【图解RabbitMQ-5】RabbitMQ Web管控台图文介绍
SLAM建图路径推荐
- 原文地址:https://blog.csdn.net/sinat_30545761/article/details/132549178
