-
单正态总体和双正态总体的假设检验
1.单正态总体和双正态总体的假设检验
笔者之前的相关笔记:
1.正态总体下常见的抽样分布
2.假设检验(Hypothesis Testing)个人理解假设检验:先对总体参数提出一个假设值,利用样本信息判断这一假设是采取拒绝该假设还是无法拒绝该假设
1.1 假设检验的步骤
1.根据给定的问题,建立假设 H 0 H_0 H0(带等号的)和备择假设 H 1 H_1 H1
H 0 H_0 H0 H 1 H_1 H1 = ≠ \neq = ≥ \geq ≥ < \lt < ≤ \leq ≤ > \gt > 下图来自《统计学图鉴》
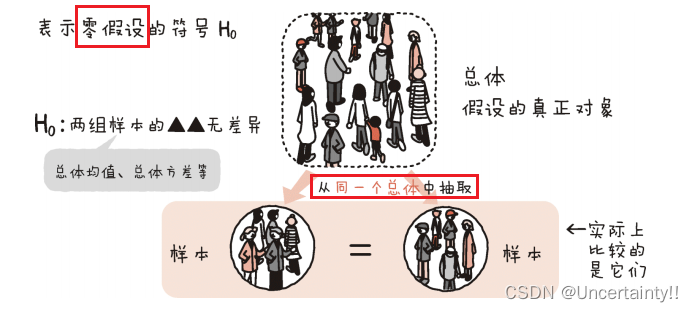
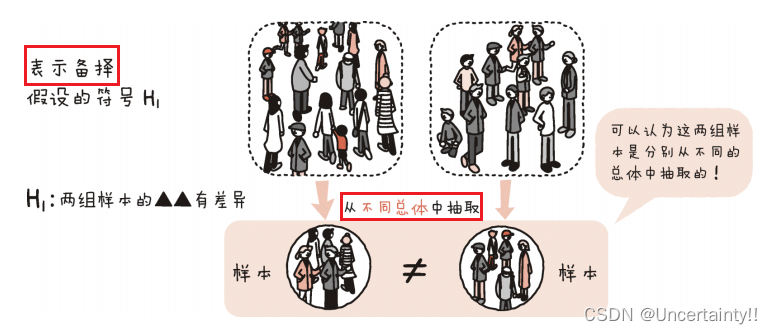
2.根据假设条件,选择合适的检验统计量 T T T,当 H 0 H_0 H0为真时,确定该统计量的分布
(1) σ 2 \sigma^2 σ2已知,检验 μ \mu μ
(2) σ 2 \sigma^2 σ2未知,检验 μ \mu μ
(3) μ \mu μ已知,检验 σ 2 \sigma^2 σ2
(4) μ \mu μ未知,检验 σ 2 \sigma^2 σ2
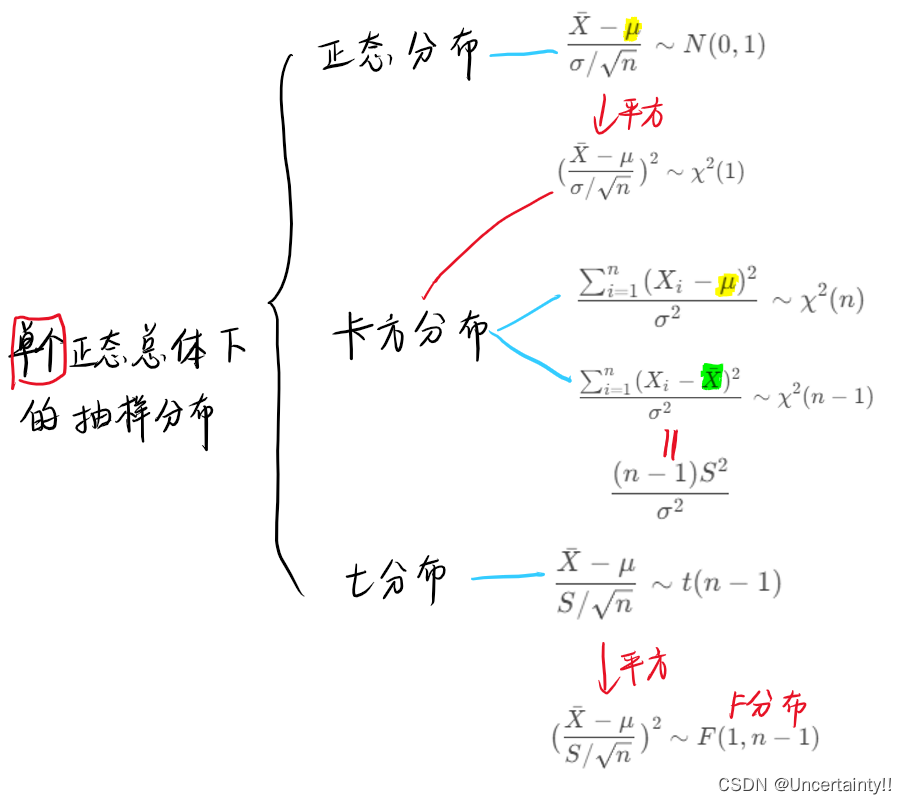
3.根据 H 1 H1 H1的形式判断使用单侧检验还是双侧检验,根据显著性水平 α \alpha α(犯第一类错误的概率)及样本容量 n n n,确定 H 0 H_0 H0的拒绝域 W W W
(总参 ≠ \neq =备择假设的参数时使用双侧检验)
(总参 > \gt >备择假设的参数时使用右侧检验)
(总参 < \lt <备择假设的参数时使用左侧检验)
下图来自:Statistics for Analytics and Data Science: Hypothesis Testing and Z-Test vs. T-Test
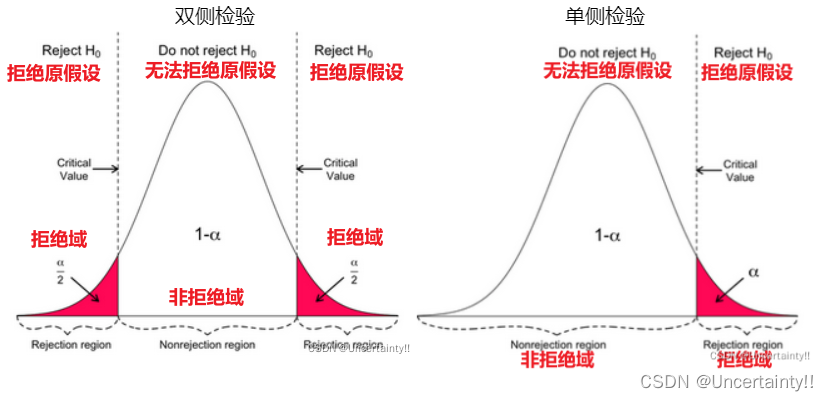
4.将样本值代入统计量 T T T中进行计算,若值落在拒绝域(小概率事件发生),则拒绝原假设 H 0 H_0 H0,若值落在接受域(大概率事件发生)则无法拒绝原假设 H 0 H_0 H0
下图来自:单侧假设检验与双侧的区别是什么?

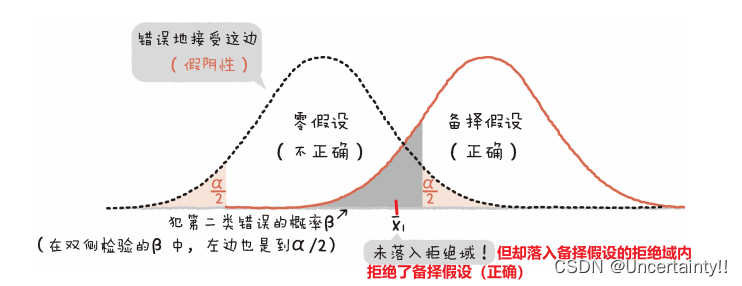
最终对假设的判断有两类错误
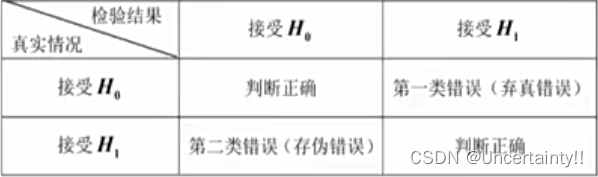
第一类错误(假阳性,弃真)
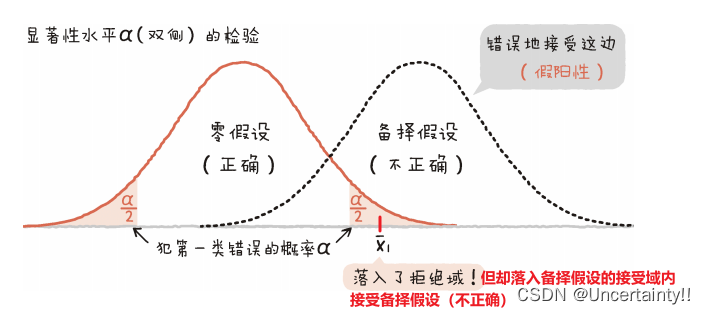
第二类错误(假阴性,存伪)
1.2 单正态总体的假设检验(对单个正态总体参数进行假设检验)
根据不同的问题,需要对 μ \mu μ或者 σ 2 \sigma^2 σ2进行检验,共四种情形
(1) σ 2 \sigma^2 σ2已知,检验 μ \mu μ

(2) σ 2 \sigma^2 σ2未知,检验 μ \mu μ
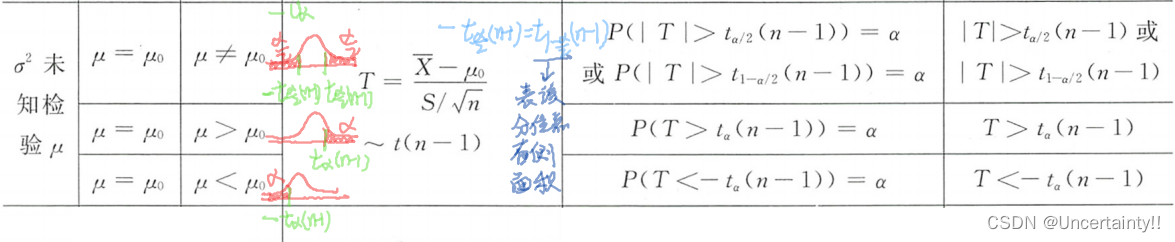
(3) μ \mu μ已知,检验 σ 2 \sigma^2 σ2

(4) μ \mu μ未知,检验 σ 2 \sigma^2 σ2

1.3 双正态总体的假设检验(对两个正态总体参数进行假设检验)

表中 S w S_w Sw的表达式
S w = ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 + n 2 − 2 S_w=\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}} Sw=n1+n2−2(n1−1)S12+(n2−1)S22
(1) σ 1 2 , σ 2 2 \sigma_1^2,\sigma_2^2 σ12,σ22已知,检验 μ 1 = μ 2 \mu_1=\mu_2 μ1=μ2

(2) σ 1 2 , σ 2 2 \sigma_1^2,\sigma_2^2 σ12,σ22未知,但 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ12=σ22,检验 μ 1 = μ 2 \mu_1=\mu_2 μ1=μ2

(3) μ 1 , μ 2 \mu_1,\mu_2 μ1,μ2未知,检验 σ 1 2 = σ 2 2 \sigma_1^2=\sigma_2^2 σ12=σ22

-
相关阅读:
Centos7 安装 Etcd
人脸识别系统——Face recognition 人脸识别
【节能学院】Acrel5000web能耗系统在某学院的应用
kafka的安装和使用
【JavaEE重点知识归纳】第7节:类和对象
学习太极创客 — MQTT 第二章(二)ESP8266 QoS 应用
【MFC】初识MFC(8)
Java 21 新特性:switch的模式匹配
pandas 基础和示例
paddle动态图自定义算子(python版)
- 原文地址:https://blog.csdn.net/weixin_48524215/article/details/131151213