G - 1-n数组

第四次题组 [Cloned] - Virtual Judge (vjudge.net)

【题目描述】

给你一个数组一个a[n]组成n正整数。您可以对其执行操作。

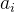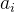在一个操作中，您可以替换数组的任何元素一个我​跟⌊/2​​⌋

看看您是否可以多次应用该操作（可能操作为0） 来制作数组一个一个成为数字的排列1自n，也就是说，以便它包含来自1自n，每个正好一次。

例如，如果a[n]=[ 1，8，25，2],n=4，那么答案是肯定的。您可以执行以下操作：

1. 取代8跟⌊8/2⌋=4,然后,a=[ 1，4，25，2].
2. 取代25跟⌊25/2⌋=12,然后,a=[ 1，4，12，2].
3. 取代12跟⌊12/2⌋=6,然后,a=[ 1，4，6，2].
4. 取代6跟⌊6/2⌋=3,然后,a=[ 1，4，3，2].

【输入】

输入数据的第一行包含一个整数t (1≤t≤104） - 测试用例的数量。

每个测试用例正好包含两行。第一个包含一个整数n (1≤n≤50），第二个包含整数a1,a2,...,an (1≤ai​≤109).

【输出】 

对于每个测试用例，在单独的行上输出：

• 是的，如果你可以制作数组一个一个成为数字的排列1自n,
• 没有其他。

在任何情况下，您都可以输出“是”和“否”（例如，字符串 yEs、yes、Yes 和 YES 将被识别为肯定响应）。

解题思路

题意是找出满足要求的数组（数组中的数字经过操作后，可以将数组中所有的数字属于1-n之间，且每个数字出现一次）。

首先要清楚，要从n找到1，也就是从大往小找。为什么呢？假设从小向大找，但是数组中的数字都能经过有限次操作后变为1，偶数都能经过操作变为2……也就是说满足操作后变为n或n-1等数字，也就一定能变为1，所以我们要从大往小找。

我首先是将数组按照从大到小排序，这一步其实可以删去。

然后遍历数组，用一个计数器统计当前找到的满足条件的数量，其中n-flag是相除后要满足的数字大小，然后将i赋值为n-flag，（n-flag下标之前的是已经满足数组条件的，接下来继续找后面的数字）。

没找到的情况，就接着往下找，找到时先将当前位置i与n-flag下标对应的数组数字交换，将n-flag放到对应的位置上去，同时i下标对应的数字a[i]也可以在循环下接着找。

代码如下

#include<iostream>
#include<algorithm>
using namespace std;
int a[55];
bool cmp(int a, int b) {
	return a > b;
}
void fun(int x, int y) {
	int t = a[x];
	a[x] = a[y];
	a[y] = t;
}
int main() {
	int t, n;
	cin >> t;
	while (t--) {
		cin >> n;
		for (int i = 0; i < n; i++) {
			cin >> a[i];
		}
		//按照从大到小排序
		sort(a, a + n, cmp);
		//判断当前有多少个已经查出来的满足题目要求的计数器
		int flag = 0;
		
		for (int i = 0; i < n; i++) {
			int x = a[i];
			while (x > n - flag) {
				x = x / 2;
			}
			//n-flag刚好是当前要找的数
			if (x == n - flag) {
				//找到之后，将数组中对应的位置与满足条件的位置交换
				fun(i, flag);
				//此时计数器自增
				flag++;
				i = flag - 1;
			}
		}
		if (flag == n) {
			cout << "YES" << endl;
		}
		else
			cout << "NO" << endl;
	}
 
}