-
蓝桥杯【第14届国赛】Python B组
倒数第二题交的时候多了一个print,只拿了国二,吐血
本题解仅代表个人观点,仅供参考,欢迎各位指正
A:弹珠堆放
【问题描述】
小蓝有 20230610 颗磁力弹珠,他对金字塔形状尤其感兴趣,如下图所示:

高度为 1 的金字塔需要 1 颗弹珠;
高度为 2 的金字塔需要 4 颗弹珠;
高度为 3 的金字塔需要 10 颗弹珠;
高度为 4 的金字塔需要 20 颗弹珠。
小蓝想要知道用他手里的弹珠可以摆出的最高的金字塔的高度是多少?
【解析及代码】
高度为 x 的金字塔需要
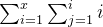 颗弹珠
颗弹珠利用等差数列的求和公式和平方差公式可简化为
 ,暴力枚举判断即可
,暴力枚举判断即可答案:494
- target = 20230610
- for i in range(1, target):
- y = (i * (i + 1) * (i + 2)) / 6
- if round(y) > target: break
- # 答案: 494
- print(i, y)
B:划分
【问题描述】
给定 40 个数,请将其任意划分成两组,每组至少一个元素。每组的权值为 组内所有元素的和。划分的权值为两组权值的乘积。请问对于以下 40 个数,划分的权值最大为多少。
5160 9191 6410 4657 7492 1531 8854 1253 4520 9231 1266 4801 3484 4323 5070 1789 2744 5959 9426 4433 4404 5291 2470 8533 7608 2935 8922 5273 8364 8819 7374 8077 5336 8495 5602 6553 3548 5267 9150 3309
在试题包中有一个名为 nums.txt 的文本文件,文件中的数与题面上的数 相同。
【解析及代码】
将这个问题等价于总边长为 2x 的矩形,如何使面积最大,那么最优的分割方法是令每条边的边长尽可能接近
以 dp[i] 表示两组权值的差值为 i 时,两个权值的具体数值,然后就是简单的一维动态规划
最后可得出两组权值都是 113462,答案:12873625444
- import itertools as it
- import math
- with open('nums.txt') as f:
- array = sorted(map(int, f.read().split()), reverse=True)
- print('length:', len(array))
- # 等价于: 总边长为 2x 的矩形, 如何使面积最大
- # 最优的分割方法是令每条边的边长尽可能接近
- dp = [(0, 0)] + sum(array) // 2 * [None]
- # 依次取出数字, 进行动态规划
- for v in array:
- new = [None] * len(dp)
- # 枚举 dp[j]: 两个和的差值为 j 时, 两个和的具体数值
- for j in filter(dp.__getitem__, range(len(dp))):
- # 最大值, 最小值
- a1, a2 = dp[j]
- # 叠加到 a1
- x1 = a1 + v
- if x1 - a2 < len(dp): new[x1 - a2] = x1, a2
- # 叠加到 a2
- x2 = a2 + v
- new[abs(a1 - x2)] = max(a1, x2), min(a1, x2)
- dp = new
- xs = next(it.dropwhile(lambda x: x is None, dp))
- # 226924 (113462, 113462) 12873625444
- print(sum(array), xs, math.prod(xs))
C:偶串
【问题描述】
小蓝特别喜欢偶数,当他看到字符串时,他总数要检查一下是不是每种字 符都是出现偶数次。给定一个字符串,请帮助小蓝检查一下该字符串是否满足 要求。
【输入格式】
输入一行包含一个字符串,由小写英文字母组成。
【输出格式】
如果字符串中的每种字符都是出现偶数次,输出大写英文单词 YES ,否则 输出大写英文单词 NO 。
【样例】
输入 输出 banana NO bbnana YES 【评测用例规模与约定】
50% 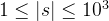
100% 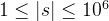
【解析及代码】
利用 Counter 暴力解决哇
- from collections import Counter
- def main():
- for i in Counter(input()).values():
- if i & 1: return False
- return True
- print('YES' if main() else 'NO')
D:交易账本
【问题描述】
小蓝最近研发了一种新的记账方式,并邀请了一些用户参加测试。交易账 本可以看作是交易记录的集合,每条交易记录都有着一个独一无二的交易编号 txId (编号大小反映了交易记录产生的时间顺序,txId 小的交易记录先发生于 txId 大的交易记录),每条交易记录包含一个或多个输入信息以及一个或多个输 出信息。
其中输入来自于已经发生过的某比交易的某个输出,可以理解为这笔钱从 某比交易输出后继续输入到了当前这比交易中,输入信息主要包含以下数据: fromTxId、fromTxOutNumber ,这表示当前输入来自于交易编号为 fromT xId 的第 fromTxOutNumber (fromTxOutNumber = 0, 1, 2, · · ·) 个输出;输出信息主 要包含以下数据:account、val ,表示将 val 数目的钱转移到了账户编号为 account 的账户上。注意,当 fromTxId 和 fromTxOutNumber 都为 −1 时,表明这是一笔特殊交易,由系统账户直接产生输出,特殊交易只含有一个输入和 一个输出,可以认为系统账户拥有无限多数目的钱,特殊交易一定可以成功。
一个合法的账本应满足以下条件:1)对于每笔交易记录,所有的输入中涉 及到的钱的总数目应和所有输出中钱的总数目相等;2)交易中的一个输出要么 不使用,要使用的话输出中的钱应该全部分配给下一个输入,而不能分配给多 个输入(特殊交易除外);3)交易按照顺序进行,不可以在某比交易中引用还 未发生的交易。
现在已知一共有 N 个不同的账户,初始时所有账户钱数目都为 0 ,账本上 总计有 M 条交易记录(按照交易完成的顺序进行记录),请你来判断下账本上 的记录是否是合法的。
【输入格式】
输入的第一行包含一个整数 T ,表示有 T 组输入数据。 对于每组输入数据:
第一行包含两个整数 N, M ,用一个空格分隔,分别表示账户的数目和 账本的交易记录数目,其中账户编号为 0, 1, 2, · · · , N − 1 ,交易记录编号为 0, 1, 2, · · · , M − 1 。
接下来 M 行,每行包含一条交易记录的信息,交易记录编号依次为 0, 1, 2, · · · , M − 1 。第一个整数 inCount 表示输入的个数,接下来包含 inCount 个输入信息,每个输入信息包含 fromTxId 和 fromTxOutNumber 两个整数;接 下来包含一个整数 outCount 表示输出的个数,然后接着包含 outCount 个输出 信息,每个输出信息包含 account 和 val 两个整数。
【输出格式】
对于每组输入数据输出一行,如果账本记录合法则输出英文单词 YES ,否 则输出英文单词 NO。
【样例】
输入 输出 说明 4
3 3
1 -1 -1 1 0 100
1 0 0 2 1 50 2 50
2 1 0 1 1 1 2 100
3 3
1 -1 -1 1 0 100
1 0 0 2 1 50 2 50
2 1 0 1 1 1 2 150
3 3
1 -1 -1 1 0 100
1 0 0 2 1 50 2 50
3 0 0 1 0 1 1 1 2 200
3 3
1 -1 -1 1 0 100
2 0 0 2 0 2 1 100 2 100
1 -1 -1 1 2 100
YES
NO
NO
NO
对于第一个数据:第一条交易 (txId = 0) 为特殊交易,给账户 0 转入了 100;第二条交易 (txId = 1) 将上一条交易的唯一一个输出作为当前交易的输 入,有两个输出,分别给账户 1 和 2 转入了 50 ;最后一条交易 (txId = 2) 将上 一条交易的两个输出作为当前交易的输入,给账户 2 转入了 100 。
对于第二个数据,第三条交易中输入与输出总额不相等。
对于第三个数据,第一条交易中的输出被使用了超过一次。
对于第四个数据,第二条交易中引用了还未发生的交易的输出。
【评测用例规模与约定】
100% 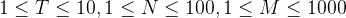

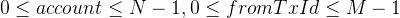
【解析及代码】
这道题没有什么难度,就是堆代码
- for _ in range(int(input())):
- n, m = map(int, input().split())
- memory = []
- for _ in range(m):
- __info = map(int, input().split())
- # fromTxId, fromTxOutNumber
- in_dat = [[next(__info) for _ in range(2)] for _ in range(next(__info))]
- # accout, val, exist
- out_dat = [[next(__info) for _ in range(2)] + [True] for _ in range(next(__info))]
- # 存储该交易信息
- memory.append([in_dat, out_dat])
- # 如果不是特殊交易, 判断是否合法
- try:
- for idx, (in_dat, out_dat) in enumerate(memory):
- if in_dat[0] != [-1, -1]:
- in_cnt = 0
- for f, i in in_dat:
- assert f < idx, f'该交易还未发生 {f} -> {idx}'
- tmp = memory[f][1][i]
- assert tmp[2], f'该输出已被占用 {tmp}'
- memory[f][1][i][2] = False
- in_cnt += tmp[1]
- out_cnt = sum(x[1] for x in out_dat)
- assert in_cnt == out_cnt, f'输入输出不符 {in_cnt}, {out_cnt}'
- print('Yes')
- except Exception as e:
- print('NO')
E:背包问题
【问题描述】
小蓝是一位狂热的积木爱好者,家里堆满了自己用积木组装的建筑模型。 最近,有两款新出的积木组件上市,小蓝自然不会错过,他带上了自己的三个 背包来到了积木商城,打算将尽可能多的积木组件带回家,每个背包都有一个 固定的空间大小。小蓝只会购买这两种新出的积木组件 A 和 B ,A 和 B 各自会 占用背包的一部分空间,但对于同一种类型的积木占用的空间是相同的。小蓝 想知道自己最多能带走多少数量的积木组件。
可以认为小蓝有足够的货币,只要背包可以装下的积木他都有能力购买。 商场内的积木数量也是有限制的。
【输入格式】
输入的第一行包含一个整数 T ,表示有 T 组独立的询问。
每一组询问由三行组成。
每组询问的第一行包含三个整数 B1, B2, B3 ,相邻的整数之间使用一个空格 分隔,表示三个背包的空间大小。
每组询问的第二行包含两个整数 cntA, cntB ,用一个空格分隔,分别表示商 场内积木组件 A 和 B 的总量。
每组询问的第三行包含两个整数 VA, VB ,用一个空格分隔,分别表示每个 积木组件 A 和 B 所占用的空间大小。
【输出格式】
输出 T 行,每行包含一个整数表示答案。
【样例】
输入 输出 说明 3
2 2 3
1 2
1 2
3 8 3
3 4
4 2
6 8 7
10 10
5 1
3
5
12
对于第一组询问,第一个背包装一个 B 积木,无剩余空间;第二个背包装 一个 B 积木,无剩余空间;第三个背包装一个 A 积木,剩余 2 空间,但积木已 经没有了;最终答案是 3 ,可以带走所有的积木。
对于第二组询问,第一个背包和第三个背包各自装一个 B 组件,第二个背 包装两个 B 组件和一个 A 组件,答案是 5 。
对于第三组询问,第一个背包:1A+1B;第二个背包:8B;第三个背包: 1A+1B。答案是 12 。
【评测用例规模与约定】
30% 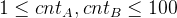
100% 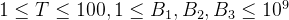
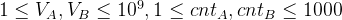
【解析及代码】
F:翻转
【问题描述】
小蓝制作了 n 个工件,每个工件用一个由小写英文字母组成的,长度为 2 的字符串表示,第 i 个工件表示为 si 。小蓝想把 n 个工件拼接到一起,方便转 移到另一个地方完成下一道工序,而拼接后的工件用字符串 S = s1 + s2 +...+ sn 表示,其中 + 表示一种奇特的拼接方式:对于 c = a + b 来说,如果 a 的第二 个字符和 b 的第一个字符相同,则拼接后的结果 c 长度为 3 而不是 4 ,中间相 同的字符可以省略一个,比如 xy + yz = xyz 而 xy + zy = xyzy 。小蓝为了让拼 接后的字符串 S 的长度尽量小,可以将若干个工件进行左右翻转之后再进行拼 接,请问拼接后的字符串 S 的最小长度是多少?
请注意所有工件必须按出现顺序依次拼接,可以翻转任意工件。
【输入格式】
输入的第一行包含一个正整数 n 。
接下来 n 行,每行包含一个长度为 2 字符串,依次表示 s1, s2, · · · , sn 。
【输出格式】
输出一行,包含一个整数表示答案。
【样例】
输入 输出 说明 3
ab
cb
zz
5 将 s2 翻转后,拼接结果为 abczz ,长度为 5 【评测用例规模与约定】
20% 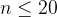
100% 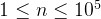
【解析及代码】
- n = int(input())
- subs = [input() for _ in range(n)]
- # e.g.: ax, ba, cb
- for i in range(1, n):
- # 翻转上一个工件
- if subs[i - 1][0] in subs[i]:
- subs[i - 1] = subs[i - 1][::-1]
- # 翻转当前的工件
- if subs[i][1] == subs[i - 1][1]:
- subs[i] = subs[i][::-1]
- # 拼接并得到答案
- res = subs.pop(0)
- for x in subs:
- res += x[1] if res[-1] == x[0] else x
- print(len(res))
G:最大阶梯
【问题描述】
小蓝特别喜爱阶梯图案,阶梯图案可以看做是由若干个大小和颜色都相同 的方格组成的,对于大小为 N 的阶梯图案,包含了 N 个连续的列,其中第 i 列 恰好有 i(1 ≤ i ≤ N)个方格,将这 N 列的底部对齐后便组成了一个阶梯图案, 将其按照 90 度旋转若干次后仍是阶梯图案,下图展示了几个不同大小的阶梯图案:

小蓝有一块大小为 H × H 的布匹,由 H × H 个大小相同的方格区域组成, 每一个方格都有自己的颜色。小蓝可以沿着方格的边缘对布匹进行裁剪,他想 要知道自己能得到的最大的同色阶梯图案的大小是多少?
【输入格式】
输入的第一行包含一个整数 H 表示布匹大小。
接下来输入 H 行,每行包含 H 个整数,表示每个方格的颜色。
【输出格式】
输出一行包含一个整数表示答案。
【样例】
输入 输出 5
0 2 1 1 0
0 0 2 2 0
0 0 1 1 1
0 0 1 1 1
2 1 1 0 2
3 【评测用例规模与约定】
30% 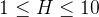
60% 
100% 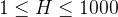
【解析及代码】
将一个方阵分成以下 4 块,编写 valtrig 函数分别验证每一块的颜色是否相同,当 0 和 3 中的任意一块 + 1 和 2 中的任意一块即为阶梯图案

然后使用二分答案枚举方阵的高度 (即阶梯图案的大小),并通过枚举方阵的左上顶点进行搜索
- h = int(input())
- array = [list(map(int, input().split())) for _ in range(h)]
- def valtrig(arr, idx):
- mid, v = len(arr) // 2, set()
- # 左、右半区
- if idx in (0, 3):
- for r in range(len(arr)):
- for c in range(r + 1 if r < mid else len(arr) - r):
- if idx == 3: c = len(arr) - 1 - c
- v.add(arr[r][c])
- if len(v) > 1: return False
- # 上、下半区
- elif idx in (1, 2):
- for c in range(len(arr)):
- for r in range(c + 1 if c < mid else len(arr) - c):
- if idx == 2: r = len(arr) - 1 - r
- v.add(arr[r][c])
- if len(v) > 1: return False
- return True
- def search(x):
- # 枚举左上顶点, 计算方阵边界
- for l in range(h):
- r = l + x
- if r <= h:
- for t in range(h):
- b = t + x
- if b <= h:
- arr = [row[l: r] for row in array[t: b]]
- # 左右任意半区 + 上下任意半区 = 阶梯图案
- if (valtrig(arr, 0) or valtrig(arr, 3)) and (
- valtrig(arr, 1) or valtrig(arr, 2)): return True
- return False
- l, r = 1, h
- # 二分答案
- while l + 1 != r:
- mid = (l + r) // 2
- if search(mid):
- l = mid
- else:
- r = mid
- print(l)
H:最长回文前后缀
【问题描述】
给定一个字符串 S ,请找出 S 的一个前缀和后缀,使得它们拼接后是一个 回文串。
请输出这个串的最长长度。
【输入格式】
输入一行包含一个字符串 S ,由小写英文字母组成。
【输出格式】
输出一行包含一个整数表示答案。
【样例】
输入 输出 说明 aababa 7 选择前缀 aababa 和后缀 a 可以得到 aababaa 【评测用例规模与约定】
30% 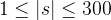
60% 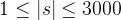
100% 
【解析及代码】
不懂,直接暴力骗分 (有佬说可以用 manacher,有空再摸索)
- def main():
- s = input()
- for x in range(len(s) * 2, 1, -1):
- # 枚举前缀的长度
- for i in range(max(1, x - len(s)),
- min(len(s) + 1, x)):
- # 后缀的长度: x - i
- tmp = s[:i] + s[i - x:]
- if tmp == tmp[::-1]: return x
- return 1
- print(main())
I:贸易航线
【问题描述】
小蓝要带领一支船队依次经过 n 个地点。小蓝的船上可以携带 k 单位的商品,商品共有 m 种,在每个地点的价格各不相同,部分商品在部分地区无法交易。
一开始小蓝的船是空的,小蓝可以在每个地点任意地买入各种商品,然后 在之后经过的地点卖出。小蓝的钱很多,你可以认为小蓝买入商品时只会受到 船队的容量的限制。
问小蓝到达终点时的最大收益是多少。
【输入格式】
输入的第一行包含三个整数 n, m, k ,相邻的整数之间使用一个空格分隔。
接下来 n 行,每行包含 m 个整数,其中第 i 行的第 j 个数
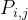 表示在第 i 个地点第 j 种商品的价格。特别地,值为 −1 表示该商品在这个地区无法交易。
表示在第 i 个地点第 j 种商品的价格。特别地,值为 −1 表示该商品在这个地区无法交易。【输出格式】
输出一行包含一个整数表示答案。
【样例】
输入 输出 7 4 4
1 2 3 6
-1 2 3 4
-1 2 4 4
3 3 2 2
2 5 3 1
1 3 3 2
1 2 4 2
24 【评测用例规模与约定】
20% 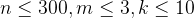
40% 
100% 
【解析及代码】
因为货物和钱是无限的,只有容量是有限的,所以只有两种状态:空载、满载某一种货物
以 dp[i] 表示载满第 i 种货物时的收益,额外增加 dp[-1] 表示空载时的收益
每到达一个地点,先把所有的货物卖出,把满载某一种货物的状态 dp[:-1] 传递到 dp[-1],得到空载时的最优状态
然后再买入货物,把 dp[-1] 传递到 dp[:-1] 得到满载某一种货物的最优状态
- n, m, k = map(int, input().split())
- # dp[-1] 表空载, dp[i] 表载满第 i 种货物时的收益
- dp = m * [-float('inf')] + [0]
- for _ in range(n):
- price = tuple(map(lambda x: int(x) * k, input().split()))
- # 满载时, 卖出不买入
- for i, p in enumerate(price):
- if p > 0: dp[-1] = max(dp[-1], dp[i] + p)
- # 空载时再买入
- for i, p in enumerate(price):
- if p > 0: dp[i] = max(dp[i], dp[-1] - p)
- print(dp[-1])
J:困局
【问题描述】
小蓝发现有个小偷在坐标 0 处,正在往 x 轴正方向逃离并保持逃离方向不 变。小蓝不想让他快速逃离(即走到坐标 n + 1 处),准备设立 k 道双向传送门 拖延其时间,每道传送门可以连接 x 轴上的两个不同的整点坐标 p ↔ q ,其中 p, q ∈ [1, n] ,同时每个坐标上最多作为一道传送门的端点。
当小偷达到一个整点时,如果其上有传送门,则会触发传送门到达传送门 另一端,当然同一个传送门不能连续触发,当无法传送时小偷会保持向 x 轴正 方向移动。小蓝想通过设置这些传送门使得小偷被至少传送 2k 次,请问有多少 种设置传送门的方式可以完成目标?
【输入格式】
输入一行包含两个正整数 n, k ,用一个空格分隔。
【输出格式】
输出一行,包含一个整数表示答案。答案可能很大,请输出答案对 998244353 取模的结果。
【样例】
输入 输出 说明 5 2 5 其中一种连接方式为 1 ↔ 4, 2 ↔ 5 ,
小偷的行走路线为 0 → 1 → 4 → 5 → 2 →
3 → 4 → 1 → 2 → 5 → 6 ,一共被传送了 4 次。
【评测用例规模与约定】
20% 
100% 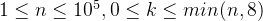
【解析及代码】
-
相关阅读:
(附源码)springboot养老院系统 毕业设计 645488
apache log4j2vulfocus靶场漏洞复现
力扣每日一题 6/10
MySQL事务和索引
解决安装sentry执行install.sh卡住的问题
Python 中的安全密码处理
VUE3 TypeError: defineConfig is not a function
switchhosts怎么配置host?
老哥们平日是怎么排查线上问题的?
哪类人群更应注重婚前协议
- 原文地址:https://blog.csdn.net/qq_55745968/article/details/131141353