MATLAB连续LTI系统的时域分析（十）

目录

1、实验目的：

2、实验内容：

---

1、实验目的：

1）掌握利用MATLAB对系统进行时域分析的方法；

2）掌握连续时间系统零输入响应的求解方法；

3）掌握连续时间系统零状态响应、冲激响应和阶跃响应的求解方法；

4）掌握利用计算机进行卷积积分和卷积和计算的方法。

2、实验内容：

2-1）、已知某系统可以由如下微分方程描述y′′(t)+ y′(t)+6y(t)=x(t)，利用MATLAB绘出该系统冲激响应和阶跃响应的时域波形。（注：题中时域范围可取[0 10]，参考函数tf、impulse、step）

a = [1 1 6]; b = [1];      %微分方程左右两端多项式的系数矩阵
time = 0:0.01:10;          %时域范围[0 10]
sys = tf(b,a);
y1 = impulse(sys,time);    %系统的冲激响应
y2 = step(sys,time);       %系统的阶跃响应
subplot(1,2,1), plot(time,y1), xlabel('时间t'), title('冲激响应');
subplot(1,2,2), plot(time,y2), xlabel('时间t'), title('阶跃响应');

2-2）、编程实现如下图所示的两个波形的卷积，并绘制出卷积后的波形。（要求：先构建两信号卷积函数，而后通过调用该函数实现做题） 

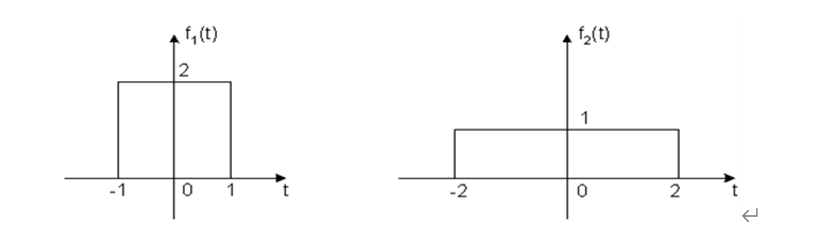
编写的卷积函数

function [t,x] = sss_conv(x1,x2,t1,t2,dt)
%文件名与函数名对应
%自写的卷积函数
x = conv(x1,x2)*dt;
t0 = t1(1) + t2(1);
L = length(x1) + length(x2)-2;
t = t0:dt:(t0+L*dt);
end

功能实现

dt = 0.01;
x1 = -1 : dt : 1; 
f1t = 2*(heaviside(x1+1) - heaviside(x1-1));
% plot(x1,f1t);
x2 = -2 : dt : 2; 
f2t = heaviside(x2+2) - heaviside(x2-2);
% plot(x2,f2t);
[t, f] = My_conv(f1t, f2t, x1, x2, dt);    %调用卷积函数
plot(t, f); 
axis([-4 4 -1 5]);

2-3）、已知系统的微分方程为：，x(t)为e-tu(t)，用数值法求零状态响应y(t)并绘图。（注：题中时域范围可取[0 10]）

a = [1 4 4]; b = [1 3]; dt = 0.1; t = 0:dt:10; % 微分方程左侧系数向量a,微分方程右侧系数向量b
[r,p] = residue(b,a); % 用residue函数（参见12.1.2节）求出其特征根p1、p2和相应的留数r1、r2
 
h = r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t);  %叠加各根分量
subplot(1,2,1), plot(t,h), title('冲激响应');
x = exp(-t);    % t已经大于0了
y = conv(x,h)*dt;   % 求x和h的卷积，长度为2*length(t)-1
subplot(1,2,2), plot(t,y(1:length(t))), title('零状态响应');

2-4）、分别用数值法和符号法求齐次微分方程在给定初始条件下的零输入响应波形，y′′(t)+2y(t)=0，y(0_)=3，y′(0_)=4。（注：题中时域范围可取[0 10]，以实现方法作为图形标题名称）

% (1)数值法
a = [1 0 2];            % 方程左端系数向量
n=length(a)-1;          % 微分方程的阶数（即根的数量）
Y0 = [3 4];             % 初始条件向量
p=roots(a);		        % 求特征方程的根
V=rot90(vander(p));     % 生成范德蒙特矩阵
C= V\Y0';	            % 求对应于各特征根的系数   左除
dt = 0.1; tf = 10;      % 时域取值范围[0 10]
t = 0:dt:tf;            % 时域取值范围[0 10]
y = zeros(1,length(t));
for k=1:n  y = y + C(k)*exp(p(k)*t); end       % 将各分量叠加，得到零输入响应的通式
subplot(121);
plot(t, y), xlabel('t'), ylabel('real(y)');    %零输入响应的实部随时间变化的趋势
title('数值法');
 
% 符号法
eq='D2y+2*y=0'; con='y(0)=3, Dy(0)=4';
y = dsolve(eq, con); y=simplify(y);
subplot(122);
ezplot(y, t);       %一定要加参数t，限制时间的范围，保证波形正确
axis([0 10 -5 5]);  % 限制xy轴范围
title('符号法'); 

2-5）、求系统，y′(0+)=-1；y(0+)=0的全响应。（注：题中时域范围可取[0 10]，参考函数tf2ss、lsim）

clear
b = [1]; a = [1 0 1];
t = 0:0.1:10; x = cos(t);
sys1 = tf(b,a);      %系统函数模型
y1 = lsim(sys1,x,t); %零状态响应
% subplot(1,2,1),plot(t,y1);
xlabel('时间');title('零状态响应');
[A B C D] = tf2ss(b,a); %系统函数模型转化成状态空间模型参数
sys2 = ss(A,B,C,D) ;zi = [-1 0]; %产生状态空间模型和初始状态矩阵
y2 = lsim(sys2,x,t,zi);          %全响应
% subplot(1,2,2);
plot(t,y2);
xlabel('时间t');title('全响应');