无监督学习——k均值

无监督学习重要的应用有两类：聚类、降维。

聚类：

• k均值

• 基于密度的聚类

• 最大期望聚类

降维：

• 潜语义分析（LSA）

• 主成分分析（PCA）

• 奇异值分解（SVD

这里主要说下k均值方法

聚类

k均值

k值是指，聚的类的个数

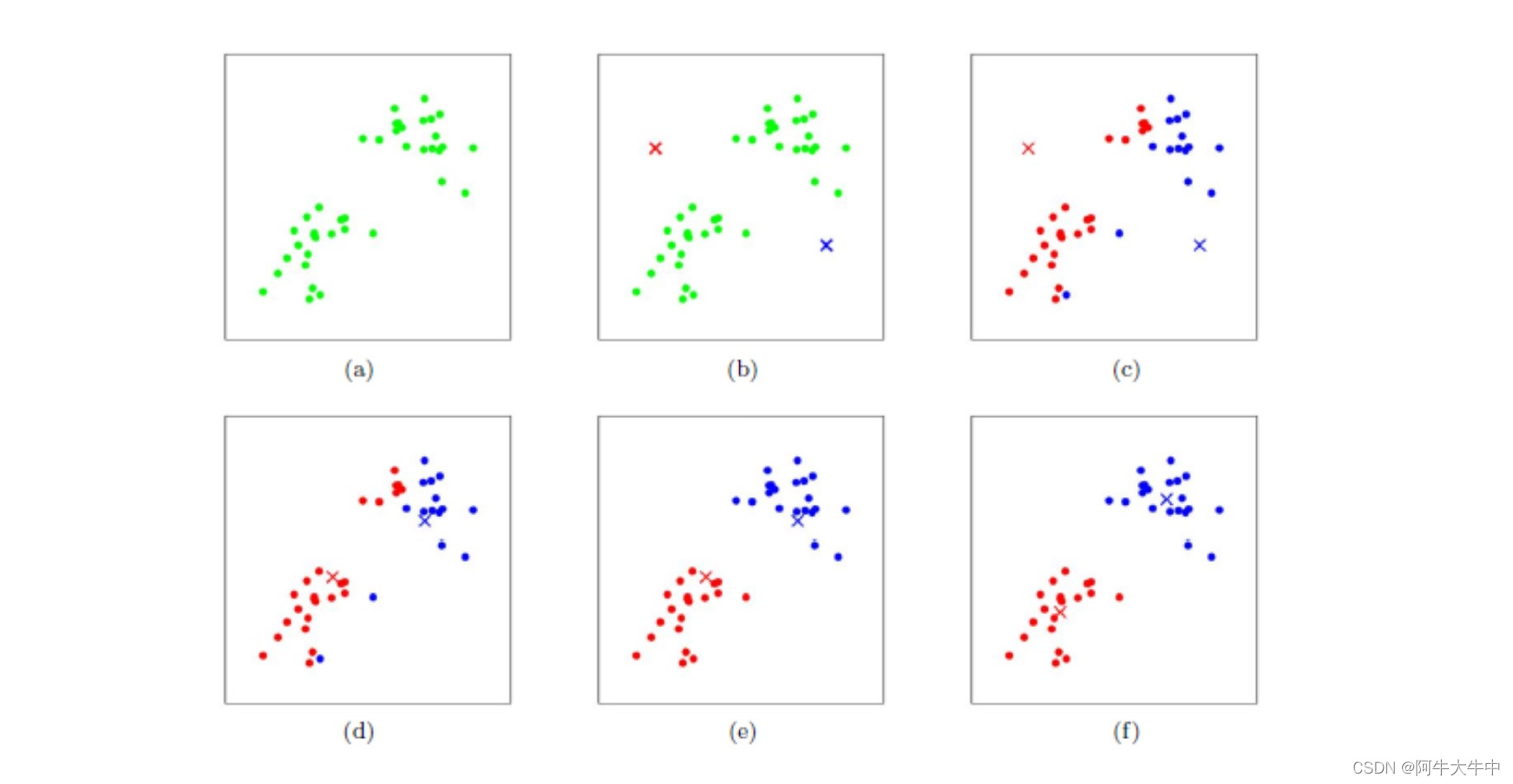
（a）原始数据

（b）随机取两个初始点（质心点）（一般是在已有的数据中选择）

（c）基于KNN近邻思想，跟谁近分到谁的那一类

（d）更新质心点（根据两类的均值）

（e）再来一轮划分

（f）更新质心点…迭代完成

• k均值（k-means）是聚类算法中最为简单、高效的，属于无监督学习算法
• 核心思想：由用户指定k个初始质心（initial centroids），以作为聚类的类别（cluster），重复迭代直至算法收敛
• 基本算法流程：
  • 选取k个初始质心（作为初始cluster）
  • repet：
    • 对每个样本点，计算得到距其最近的质心，将其类别标记为该质心所对应的cluster
    • 重新计算k个cluster对应的质心
  • until质心不在发生变化，或迭代达到上限

代码实现

1. 引入依赖

import numpy as np
import matplotlib.pyplot as plt

# 从sklearn中直接生成聚类数据
# from sklearn.datasets.samples_generator import make_blobs # 新版本更改
from sklearn.datasets import make_blobs
1
2
3
4
5
6

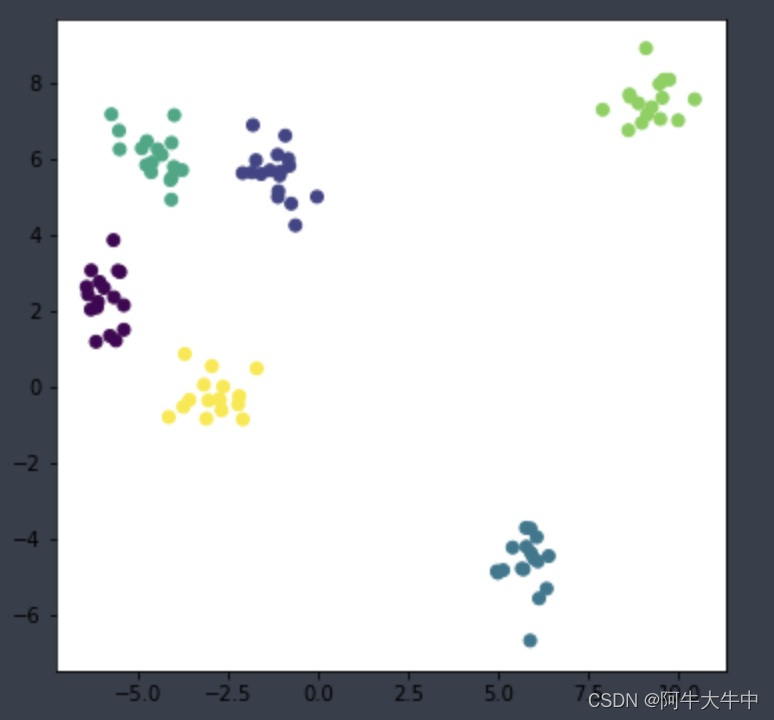
2. 数据加载

# n_sanmples表示样本点的个数，centers表示中心点的个数
x, y = make_blobs( n_samples=100, centers=6, random_state=1234, cluster_std=0.6 )
# x是100个数据点的坐标，y表示类别（y暂时没用）
plt.figure(figsize=(6,6)) # 看起来舒服点
plt.scatter(x[:,0], x[:,1], c=y) # c表示color，y取不同值有不同的颜色
plt.show()
1
2
3
4
5
6

3. 算法实现

# 引入scipy中的距离函数，默认欧式距离
from scipy.spatial.distance import cdist

class K_Means(object):
    # 初始化，参数 n_clusters（K）、迭代次数 max_iter、初始质心 centroids
    def __init__(self, n_clusters=6, max_iter=300, centroids=[]):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.centroids = np.array( centroids, dtype=np.float ) # 转化为numpy中的矩阵
        
    # 训练模型方法，k-means聚类过程，传入原始数据
    def fit(self, data):
        # 假如没有指定初始质心，就随机选取data中的点作为初始质心
        if( self.centroids.shape == (0,) ):
            # 从data中随机生成0到data行数的6个整数，作为索引值
            self.centroids = data[ np.random.randint( 0, data.shape[0], self.n_clusters ) ,: ]
            
        # 开始迭代
        for i in range(self.max_iter):
            # 1. 计算距离矩阵，得到的是一个100*6的矩阵，每一行代表一个样本点距离所有质心的距离
            distances = cdist(data, self.centroids)
            
            # 2. 对距离按有近到远排序，选取最近的质心点的类别，作为当前点的分类
            c_ind = np.argmin( distances, axis=1 )
            
            # 3. 对每一类数据进行均值计算，更新质心点坐标
            for i in range(self.n_clusters):
                # 排除掉没有出现在c_ind里的类别
                if i in c_ind:
                    # 选出所有类别是i的点，取data里面坐标的均值，更新第i个质心
                    self.centroids[i] = np.mean( data[c_ind==i], axis=0 )
    
    # 实现预测方法
    def predict(self, samples):
        # 跟上面一样，先计算距离矩阵，然后选取距离最近的那个质心的类别
        distances = cdist(samples, self.centroids)
        c_ind = np.argmin( distances, axis=1 )
        
        return c_ind
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

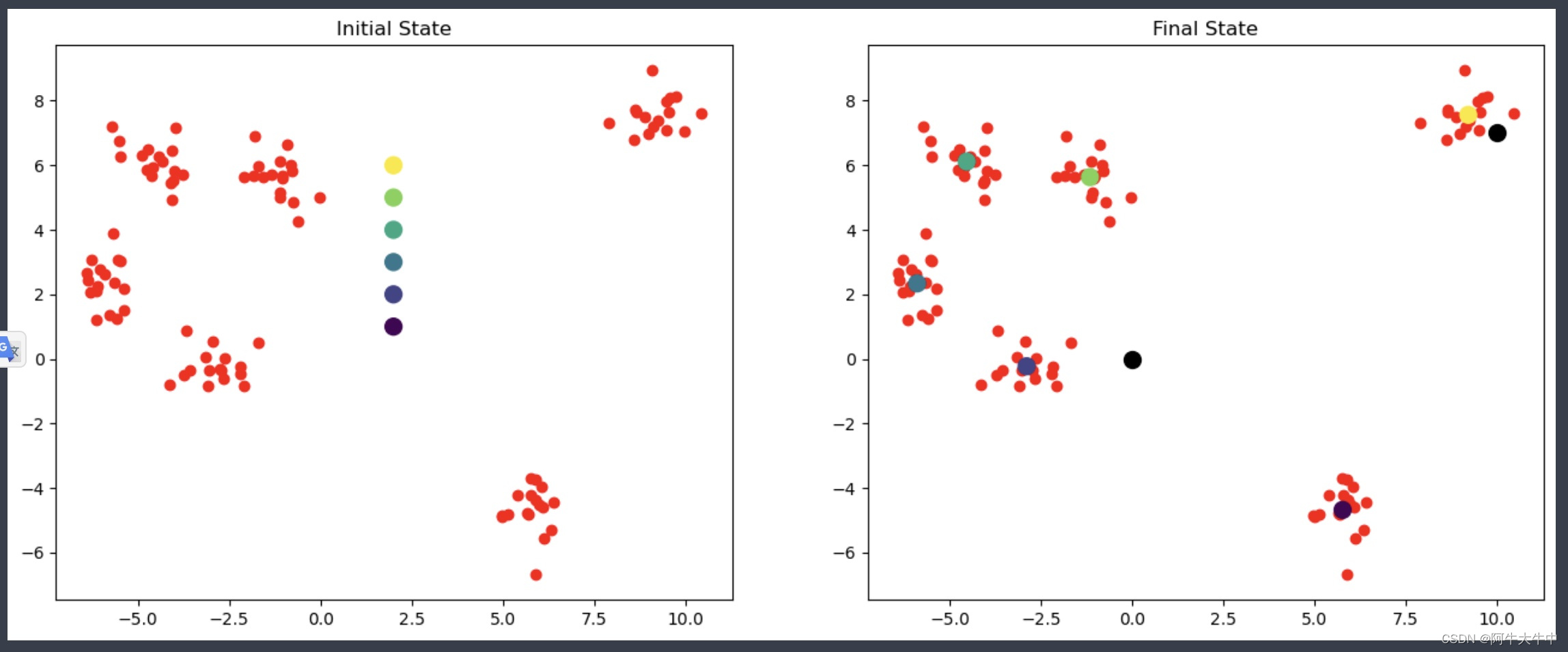
4. 测试

# 定义一个绘制子图函数
def plotKMeans(x, y, centroids, subplot, title):
    # 分配子图，121表示1行2列的子图中的第一个
    plt.subplot(subplot)
    plt.scatter(x[:,0], x[:,1], c='r')
    # 画出质心点
    plt.scatter(centroids[:,0], centroids[:,1], c=np.array(range(6)), s=100)
    plt.title(title)

kmeans = K_Means(max_iter=300, centroids=np.array([[2,1],[2,2],[2,3],[2,4],[2,5],[2,6]]))

plt.figure(figsize=(16, 6))
plotKMeans( x, y, kmeans.centroids, 121, 'Initial State' )

# 开始聚类
kmeans.fit(x)

plotKMeans( x, y, kmeans.centroids, 122, 'Final State' )

# 预测新数据点的类别
x_new = np.array([[0,0],[10,7]])
y_pred = kmeans.predict(x_new)

print(kmeans.centroids)
print(y_pred)

plt.scatter(x_new[:,0], x_new[:,1], s=100, c='black')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

输出：

[[ 5.76444812 -4.67941789]
 [-2.89174024 -0.22808556]
 [-5.89115978  2.33887408]
 [-4.53406813  6.11523454]
 [-1.15698106  5.63230377]
 [ 9.20551979  7.56124841]]
[1 5]
1
2
3
4
5
6
7