【数据结构】如何应用堆解决海量数据的问题

堆(Heap数据结构堆在计算机科学中有着广泛的应用，今天来介绍两种堆的应用：堆排序、Top-k问题🍉

堆排序

​ 堆排序是一种基于堆数据结构的排序算法。它的基本思想是，将待排序的序列构建成一个大根堆（或小根堆），然后依次取出堆顶元素（即最大值或最小值），将其放入已排序序列的末尾，再将剩余的元素重新调整为一个新的堆。重复这个过程，直到所有元素都被取出并放入已排序序列中。

具体来说，堆排序的过程如下：

1. 将待排序的长度为n序列构建成一个大根堆（或小根堆）。这个过程可以从最后一个非叶子节点开始，依次向前进行，保证每个子树都是一个大根堆（或小根堆）。
2. 取出堆顶元素（即最大值或最小值），将其放入已排序序列的末尾。
3. 将剩余（n-1）的元素重新调整为一个新的堆。
4. 重复步骤 2 和步骤 3，直到所有元素都被取出并放入已排序序列中。最终得到的序列就是排好序的。

最终得到的序列就是排好序的。

堆排序的时间复杂度为 O(nlogn)，空间复杂度为 O(1)。

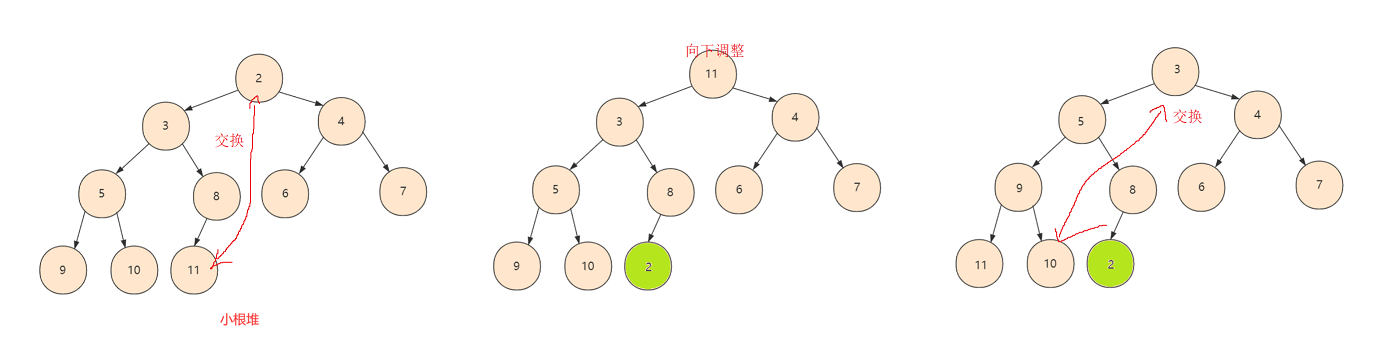
向下调整法

从非叶节点的最后一个数据的下标开始，每次取出孩子中较大或较小的数（看是大堆还是小堆）向下进行调整，由于每多一层，下层是上层的二倍，这种办法直接可以省略掉最后一层，也可以达到建堆的目的，所以这种办法为更优的办法。

由于需要向下调整，所以这种办法需要找到子节点，我们已经知道父结点的运算了，子结点就是父节点的逆运算。

结合上面所说，实现代码如下：

void AdjustDown(HeapDataType* arr, int n, int parent)//向下调整
{
	assert(arr);
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child<n - 1 && arr[child] > arr[child + 1])
		{
			child = child + 1;
		}
		if (arr[child] < arr[parent])
		{
			swap(&arr[child], &arr[parent]);
		}
		parent = child;
		child = child * 2 + 1;
	}
}

void HeapSort(int* a,int n)//堆排序
{
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		AdjustDown(a, n,i);
	}

	for (int i = n-1; i > 0; i--)
	{
		swap(&a[0], &a[i]);
		AdjustDown(a, i, 0);
	}
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
}

int main()
{
	int arr[] = { 1,4,6,2,4,8,5,8,3,111,4,5,32,44 };
	HeapSort(arr, sizeof(arr) / sizeof(int));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

Top-k问题

Top-k 问题是指在一个数据集中找到前 k 个最大（或最小）的元素。一般情况下数据量都比较大。 比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

下面是使用堆排序实现 Top-k 问题的具体步骤：

1. 创建一个大小为 k 的小根堆，用于存储当前的前 k 个最大元素。
2. 将前 k 个元素插入小根堆中。
3. 遍历剩余的元素，对于每个元素执行以下操作：
   • 如果当前元素比堆顶元素大，则将堆顶元素弹出，再将当前元素插入堆中。
4. 遍历完所有元素后，小根堆中剩余的 k 个元素就是前 k 个最大元素。

使用堆排序实现 Top-k 问题的时间复杂度为 O(nlogk)，空间复杂度为 O(k)，其中 n 是数据集的大小。这种方法适用于数据集较大的情况，但需要额外的空间来存储堆。

代码实现

• 生成一个有10000随机数的文件

void CreateNDate()	//生成一个有10000个随机数的文件
{
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	for (int i = 0; i < n; i++)
	{
		int x = rand() % 10000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

按上述步骤进行排序

void AdjustDown(HeapDataType* arr, int n, int parent)//向下调整
{
	assert(arr);
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child<n - 1 && arr[child] > arr[child + 1])
		{
			child = child + 1;
		}
		if (arr[child] < arr[parent])
		{
			swap(&arr[child], &arr[parent]);
		}
		parent = child;
		child = child * 2 + 1;
	}
}
void PrintTopK(int k)
{
	const char* file = "data.txt";
	FILE* fin = fopen(file, "r");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	int* heap = (int*)malloc(k * sizeof(int));
	int x;
	for (int i = 0; i < 5; i++)
	{
		fscanf(fin,"%d",&heap[i] );//将前k个元素放到数组里
	}
    for (int i = (k - 1 - 1) / 2; i >= 0; i--)	//将k个元素建立一个小堆
	{
		AdjustDown(heap, k, i);
	}
	while (!feof(fin))
	{
		fscanf(fin, "%d", &x);
		if (heap[0] < x)
		{
			heap[0] = x;		//将剩余n-k个元素依次与堆顶元素交换，不满则则替换

			AdjustDown(heap,k,0);
		}
	}
	fclose(fin);
	for (int i = 0; i < k; i++)
	{
		printf("%d  ", heap[i]);
	}
}

int main()
{
	CreateNDate();
	PrintTopK(10);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

✨本文收录于数据结构理解与实现

当你喜欢一篇文章时，点赞、收藏和关注是最好的支持方式。如果你喜欢我的文章，请不要吝啬你的支持，点赞👍、收藏⭐和关注都是对我最好的鼓励。感谢你们的支持！