代码随想录刷题day56 583. 两个字符串的删除操作；72. 编辑距离；编辑距离总结篇

代码随想录刷题day56 583. 两个字符串的删除操作；72. 编辑距离；编辑距离总结篇

关于编辑距离的一些题目。

583. 两个字符串的删除操作

583. 两个字符串的删除操作 - 力扣（Leetcode）

化简这一步不容易想到。原理就是两个都删除相当于删除一个再多操作一次。

还有一个思路就是求出最长公共子序列，也是一种方法。

思路

动态规划一

两个字符串可以相互删了，这种题目也知道用动态规划的思路来解，动规五部曲，分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

这里dp数组的定义有点点绕，大家要撸清思路。

2. 确定递推公式

• 当word1[i - 1] 与 word2[j - 1]相同的时候
• 当word1[i - 1] 与 word2[j - 1]不相同的时候

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

因为dp[i - 1][j - 1] + 1等于 dp[i - 1][j] 或 dp[i][j - 1]，所以递推公式可简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);

3. dp数组如何初始化

从递推公式中，可以看出来，dp[i][0] 和 dp[0][j]是一定要初始化的。

dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显dp[i][0] = i。

dp[0][j]的话同理，所以代码如下：

vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
1
2
3

4. 确定遍历顺序

从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。

所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。

5. 举例推导dp数组

以word1:“sea”，word2:"eat"为例，推导dp数组状态图如下：

以上分析完毕，代码如下：

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

动态规划二

只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

代码如下：

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));
        for (int i=1; i<=word1.size(); i++){
            for (int j=1; j<=word2.size(); j++){
                if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return word1.size()+word2.size()-dp[word1.size()][word2.size()]*2;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

72. 编辑距离

72. Edit Distance - 力扣（Leetcode）

关键是要想明白word2减一个相当于word1加一个这个原理。以及如何用递推公式的方法表示每种修改的可能。

思路

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

这里在强调一下：为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？

用i来表示也可以！ 但我统一以下标i-1为结尾的字符串，在下面的递归公式中会容易理解一点。

2. 确定递推公式

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
    不操作
if (word1[i - 1] != word2[j - 1])
    增
    删
    换
1
2
3
4
5
6

也就是如上4种情况。

if (word1[i - 1] == word2[j - 1])` 那么说明不用任何编辑，`dp[i][j]` 就应该是 `dp[i - 1][j - 1]`，即`dp[i][j] = dp[i - 1][j - 1];
1

此时可能有同学有点不明白，为啥要即dp[i][j] = dp[i - 1][j - 1]呢？

那么就在回顾上面讲过的dp[i][j]的定义，word1[i - 1] 与 word2[j - 1]相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。

在下面的讲解中，如果哪里看不懂，就回想一下dp[i][j]的定义，就明白了。

在整个动规的过程中，最为关键就是正确理解dp[i][j]的定义！

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

• 操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。

即 dp[i][j] = dp[i - 1][j] + 1;

• 操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。

即 dp[i][j] = dp[i][j - 1] + 1;

这里有同学发现了，怎么都是删除元素，添加元素去哪了。

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"， 最终的操作数是一样！ dp数组如下图所示意的：

          a                         a     d
   +-----+-----+             +-----+-----+-----+
   |  0  |  1  |             |  0  |  1  |  2  |
   +-----+-----+   ===>      +-----+-----+-----+
 a |  1  |  0  |           a |  1  |  0  |  1  |
   +-----+-----+             +-----+-----+-----+
 d |  2  |  1  |
   +-----+-----+
1
2
3
4
5
6
7
8

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

递归公式代码如下：

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
1
2
3
4
5
6

3. dp数组如何初始化

再回顾一下dp[i][j]的定义：

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

那么dp[i][0] 和 dp[0][j] 表示什么呢？

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

所以C++代码如下：

for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
1
2

4. 确定遍历顺序

从如下四个递推公式：

• dp[i][j] = dp[i - 1][j - 1]
• dp[i][j] = dp[i - 1][j - 1] + 1
• dp[i][j] = dp[i][j - 1] + 1
• dp[i][j] = dp[i - 1][j] + 1

可以看出dp[i][j]是依赖左方，上方和左上方元素的，如图：

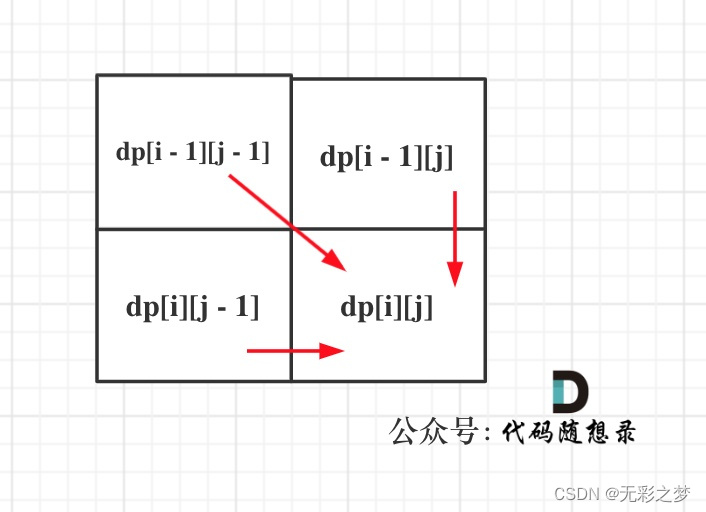
所以在dp矩阵中一定是从左到右从上到下去遍历。

代码如下：

for (int i = 1; i <= word1.size(); i++) {
    for (int j = 1; j <= word2.size(); j++) {
        if (word1[i - 1] == word2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1];
        }
        else {
            dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
        }
    }
}
1
2
3
4
5
6
7
8
9
10

5. 举例推导dp数组

以示例1为例，输入：word1 = "horse", word2 = "ros"为例，dp矩阵状态图如下：

以上动规五部分析完毕，C++代码如下：

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
                else {
                    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};
             dp[i][j] = dp[i - 1][j - 1];
                }
                else {
                    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29