acwing基础课——Dijkstra

由数据范围反推算法复杂度以及算法内容 - AcWing

常用代码模板3——搜索与图论 - AcWing

基本思想：

        迪杰斯特拉（dijkstra）算法是单源最短路径问题的求解方法,它是一个按路径长度递增的次序产生最短路径的算法。单源最短路径就在给出一个固定网络，指定一个原点s，一个目标点e，求这两个点之间的最短路径。（一般稠密图我们用邻接矩阵来存储，稀疏图用邻接表来存储）

        注意一点的是，dijkstra算法不能解决负权图问题，可以参考一下这位博主大佬的讲解

(64条消息) Dijkstra算法为什么不能用于负权图_Korpse的博客-CSDN博客_dijkstra算法为什么不能用于负权值

        下列图示演示了Dijkstra算法的实现，将图中的点不断加入到S（S:当前已经确定了最短路径的点）中使得各个点都确定其最短路径，每轮循环我们都是用当前点去比较它所连通的点的距离能否更新，也就是比较当前点（当前点已经确定了最短路径）到连通点的距离和连通点到源点的距离大小，不断循环直到求出每一个点的最短路径就完成了我们的算法。

 

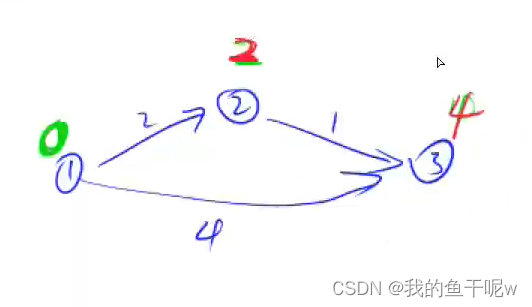
849. Dijkstra求最短路 I - AcWing题库

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n≤500
1≤m≤1e5
图中涉及边长均不超过10000。

输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

#include
#include
#include
 
using namespace std;
 
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];//集合S表示该点已经确定了最短路径，这里用false表示不在S内
 
void dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for(int i = 1; i < n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++) if(!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
        for(int j = 1; j <= n; j++) dist[j] = min(dist[j], dist[t] + g[t][j]);
        st[t] = true;
        //找到S外的路径最短的点，用它来更新一遍所连通的点的距离，并将其添加到S里
    }
}
 
int main()
{
    memset(g, 0x3f, sizeof g);
    
    cin >> n >> m;
    
    while(m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);//图中可能存在重边和自环
    }
    
    dijkstra();
    
    if(dist[n] == 0x3f3f3f3f) cout << "-1";
    else cout << dist[n];
    
    return 0;
}

例题：

850. Dijkstra求最短路 II - AcWing题库 //稀疏图用邻接表来存 并用小根堆来进行优化

743. 网络延迟时间 - 力扣（LeetCode）