leetcode：1203. 项目管理【双topo：组间topo + 组内topo】

题目截图

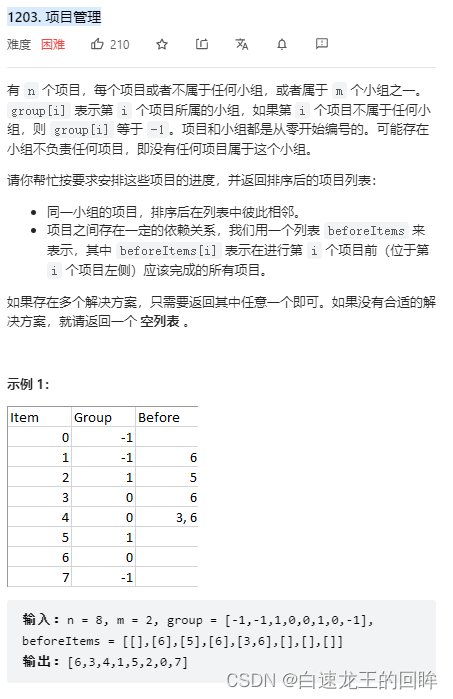
题目分析

• 没有第一个条件，就是简单topo排序
• 有了第一个条件，每个小组都需要完全隔开，因此不同小组间也需要一个topo排
• step1：对于group为-1的自成一组
• step2：建图，组内以及组间，对于beforeItems的关系，通过groupId判断是组间还是组内
• step3：topo check函数
• step4：先判断组间能否完成topo，记录inter_topo顺序
• step5：按照inter_topo再各自判断inner_topo,如果全部inner_topo都合法，合成whole_topo即可

ac code

class Solution:
    def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:
        # 同一小组的项目，排序后在列表中彼此相邻 -> 组间topo
        # 全局topo = 组间topo + 组内topo

        # step1: 补充分组信息
        groupIndex2groupMember = defaultdict(list)
        for i in range(n):
            if group[i] == -1:
                group[i] = m
                m += 1
            groupIndex2groupMember[group[i]].append(i)
        
        # step2: 组间和组内建图
        inter = defaultdict(list)
        inner = defaultdict(lambda: defaultdict(list))
        for i in range(n):
            for j in beforeItems[i]:
                # j -> i
                if group[i] == group[j]: # 组内
                    inner[group[i]][j].append(i)
                else: # 组间
                    inter[group[j]].append(group[i])
        
        # step3: topo排序check
        def check_topo(g, nodes):
            indeg = defaultdict(int)
            for x in g:
                for y in g[x]: # y入度+1
                    indeg[y] += 1
            q = [i for i in nodes if indeg[i] == 0]
            topo_ans = q[:]
            while q:
                new_q = []
                for qq in q:
                    for next_node in g[qq]:
                        indeg[next_node] -= 1
                        if indeg[next_node] == 0:
                            topo_ans.append(next_node)
                            new_q.append(next_node)
                q = new_q
            #print(topo_ans)
            return topo_ans if len(topo_ans) == len(nodes) else []
        
        # step4: 组间check
        inter_topo = check_topo(inter, list(set(group))) # 不能用range(m), 可能中间有空位
        if len(inter_topo) == 0:
            return []
        
        # step5: 组内check, 逐一check
        whole_topo = []
        for idx in inter_topo: # 按照inter_topo取出group的idx
            #print(idx, inner[idx], groupIndex2groupMember[idx])
            inner_topo = check_topo(inner[idx], groupIndex2groupMember[idx])
            #print(inner_topo)
            if len(inner_topo) == 0:
                return []
            whole_topo.extend(inner_topo)
        return whole_topo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

总结

• 学到了一个二维defaultdict的写法：
  • inner = defaultdict(lambda: defaultdict(list))
• 组间组内topo，关键是通过同组要连续放，想到组间topo
• 然后组内topo就很自然了