-
空间直接坐标系(XYZ)转经纬度(BLH)
本章首先介绍空间直角坐标系与大地坐标系,然后列出XYZ转换BLH的公式,最后基于C语言完成该部分代码设计。
参考书籍:
董大男,陈俊平,王解先等,GNSS高精度定位原理,科学出版社
黄丁发,熊永良,周乐韬等,GPS卫星导航定位技术与方法,科学出版社。
公式原理
空间直角坐标系
空间直角坐标系原点位于参考椭球的中心,Z轴指向参考椭球的北极,X轴指向首子午面与赤道的交点,Y轴位于赤道面上,且按右手坐标系与X轴呈90°夹角。某点在空间中坐标可用该店在次坐标系的各个坐标轴上的投影来表示。(如下图所示)
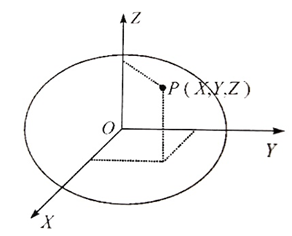
空间直角坐标系
大地坐标系
空间大地坐标系是采用大地经纬度和大地高来描述空间位置的(下图)。维度是指P点的法线与赤道面的夹角,用B(-90°~ 90°)表示,向北为正称为北纬,向男为负称为南纬。经度是指P点的参考椭球子午面与起始子午面的二面角,用L表示(-180°~180°),由起始子午面起算,向东为正称为东京,向西为负称为西经。大地高是空间点沿该法线到椭球面的距离,用H表示,向上为正,向下为负。
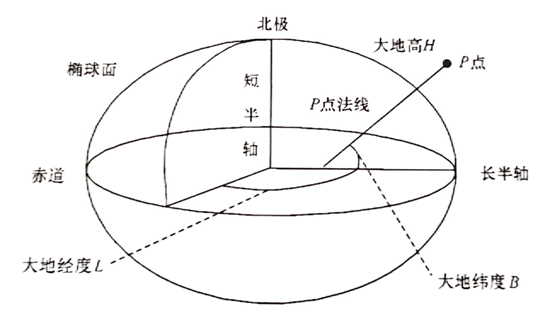
空间大地坐标系
XYZ转BLH
空间直角坐标系(X,Y,Z)与大地坐标系 (B,L,H)关系如下:
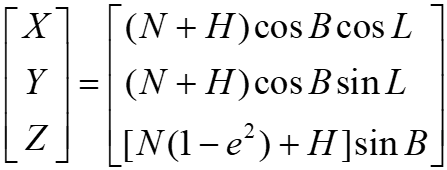
式中:N为某点P的卯酉圈半径;(B,L,H)为P点的大地坐标系,卯酉圈半径N公式如下:
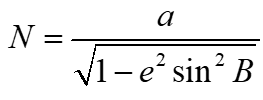
式中:a为椭球长半轴,b为椭球短半轴,
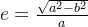 为第一离心率,B为大地维度。不难看出,大地维度是关于自身的函数,需要迭代求解。计算方式如下:
为第一离心率,B为大地维度。不难看出,大地维度是关于自身的函数,需要迭代求解。计算方式如下: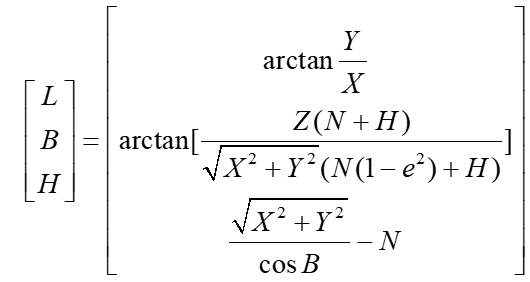
初始迭代时,设:
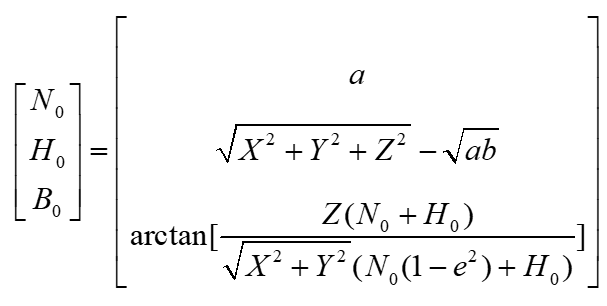
于是:
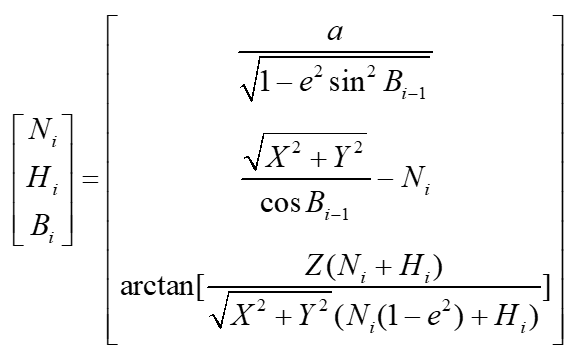
当ΔH<0.001m,B的经度保证在0.001秒即可停止迭代。
关于上述代码的详细推导过程,请参考charlee44博主的大地经纬度坐标与地心地固坐标的的转换
程序设计
- #define a 6378137.0//长半轴
- #define f (1 / 298.257223563)//扁率
- #define e2 (f*(2-f))//第一偏心率平方
- //经纬度转换(弧度)
- BLH XYZtoLB(double X, double Y, double Z)
- {
- BLH res = { 0 };
- double B = 0.0, N = 0.0, H = 0.0, R0, R1, deltaH, deltaB;
- R0 = sqrt(pow(X, 2) + pow(Y, 2));
- R1 = sqrt(pow(X, 2) + pow(Y, 2) + pow(Z, 2));
- //经度直接求解
- res.L = atan2(Y, X);
- //迭代求大地维度和大地高
- N = a;
- H = R1 - a;
- B = atan2(Z * (N + H), R0 * (N * (1 - e2) + H));
- do
- {
- deltaH = N;//判断收敛所用
- deltaB = B;
- N = a / sqrt(1 - e2 * pow(sin(B), 2));
- H = R0 / cos(B) - N;
- B = atan2(Z * (N + H), R0 * (N * (1 - e2) + H));
- } while (fabs(deltaH - H) > 1.0e-3 && fabs(deltaB - B) > 1.0e-9);
- res.B = B;
- res.H = H;
- return res;
- }
这里的精度控制可以自己尝试修改一下,看看有什么不同。
其中,BLH为用于传参的结构体,代码如下:
- //经纬度函数传参
- typedef struct BLH
- {
- double B;//维度
- double L;//经度
- double H;//高
- }BLH;
代码部分与上述公式部分对应,代码并不复杂按公式来即可,求出测站的经纬度后,即可求出卫星的高度角、方位角,从而进行定权、误差改正等内容。
卫星高度角、方位角求解可参考我的博客:求解卫星高度角、方位角
补充:
在程序设计中,因为浮点数保存精度的原因,应该尽量避免乘除法,有些公示进行了简单换算,同学们先自己换算一下。
-
相关阅读:
反转链表(链表的逆置)
AlexNet网络详解
NLP 算法实战项目:使用 BERT 进行模型微调,进行文本情感分析
Baklib知识分享|文档管理促进企业成长进步
Docker 常用命令
GB28181学习(六)——实时视音频点播(数据传输部分)
自动驾驶架构
C语言之sizeof 和 strlen 详细介绍
看完阿里最新产500页微服务架构笔记,感觉我格局太小
vue指令(代码部分二)
- 原文地址:https://blog.csdn.net/why1472587/article/details/128190538
