字符串处理【字典树】 - 原理 字典树详解

字符串处理【字典树】 - 原理 字典树详解

字典树，又称Trie树、单词查找树，是一种树形结构，也是哈希树的一种变种，主要用于统计、排序和存储大量的字符串（但不限于字符串），所以经常被搜索引擎系统用于文本词频统计。

它的优点：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

字典树是用于字符串快速检索的多叉树，每个节点都包含多个字符指针，将从根节点到某一节点路径上经过的字符连接起来，为该节点对应的字符串。

例如，bee是一个单词，beer也是一个单词，此时可以在每个单词结束的位置都加一个end[]标记，表示从根到这里有一个单词。

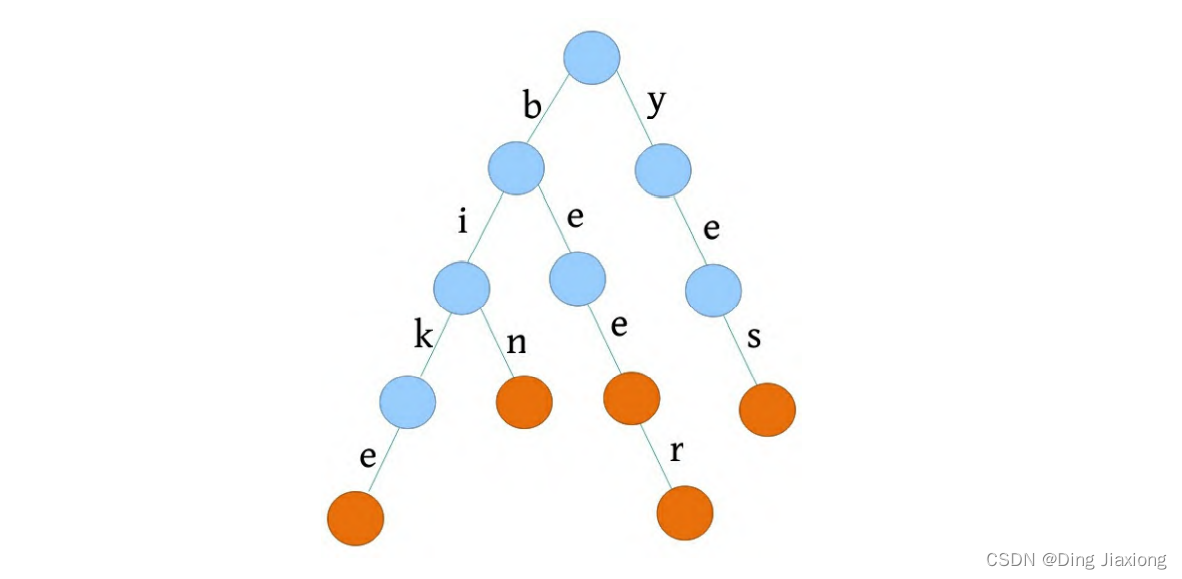
字典树的基本操作： 创建、查找、插入和删除，极少出现删除操作。

【1】字典树的创建

字典树的创建指将所有字符串都插入字典树中。插入操作指将一个字符串插入字典树中。

字典树可以采用数组或链表存储，这里采用数组存储来实现静态链表。

[举个栗子]

字符串是由小写字母组成的，每个节点都包含26个域（26个字母）。

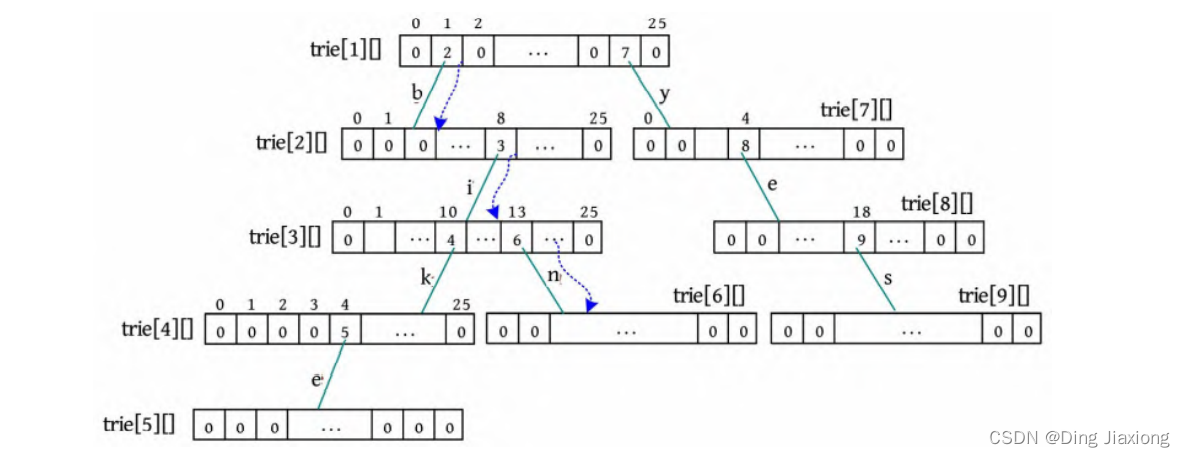
① 插入一个单词s（bike），首先将字符转换为数字，s[0]-‘a’=1，判断trie[1][1]为0，令trie[1][1]=2，相当于创建一个新的节点（下标为2）。

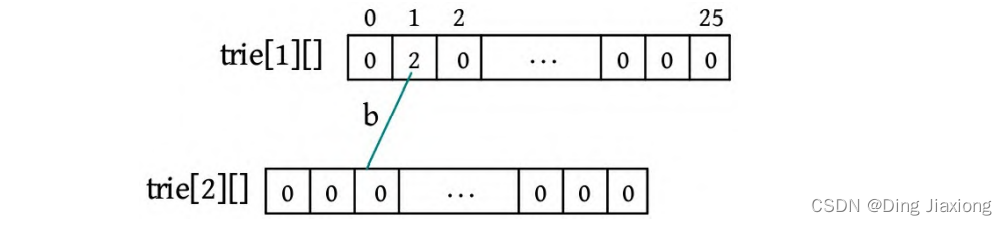
② s[1]-‘a’=8，判断trie[2][8]为0，令trie[2][8]=3。

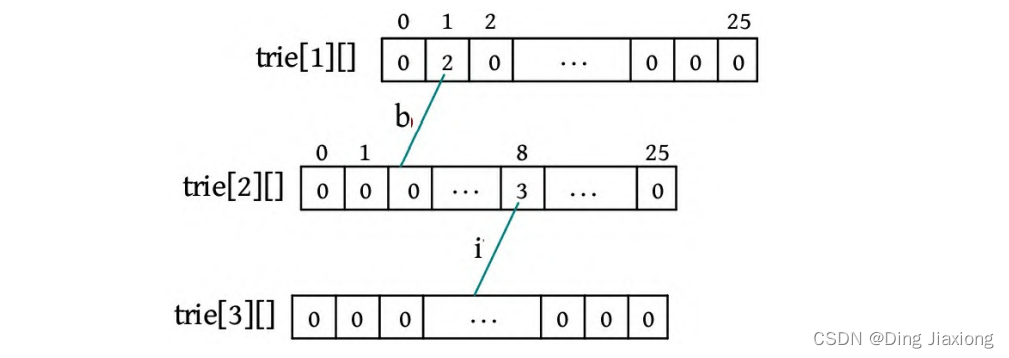
③ s[2]-‘a’=10，判断trie[3][10]为0，令trie[3][10]=4。

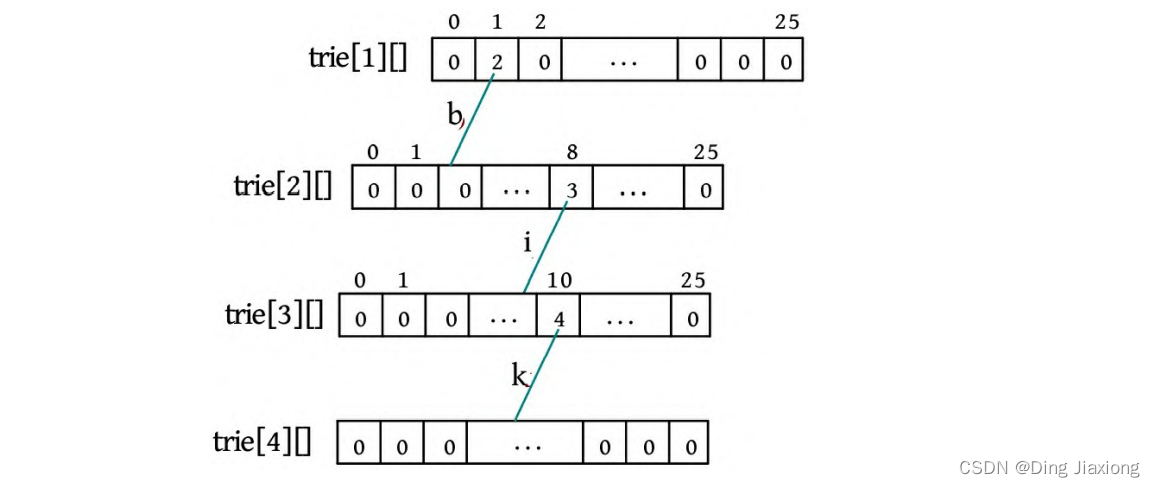
④ s[3]-‘a’=4，判断trie[4][4]为0，令trie[4][4]=5，end[5]=true，标记单词结束。

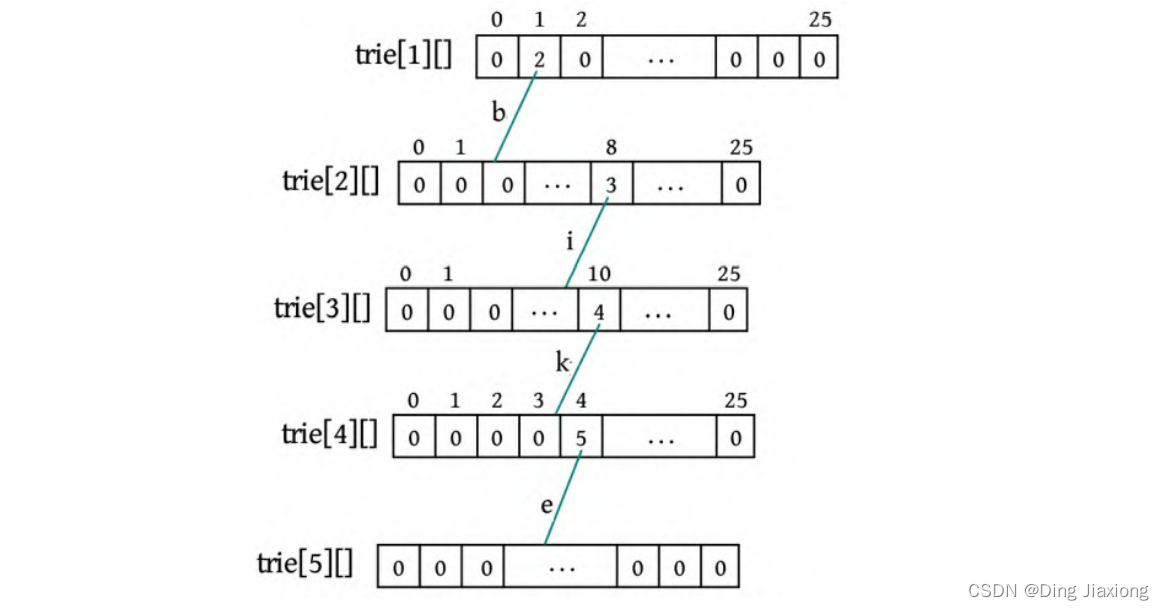
⑤ 接着插入一个单词s（bin），首先将字符转换为数字，s[0]-‘a’=1，判断trie[1][1]=2，不为0，令p =2，沿第2个节点继续插入。

⑥ s[1]-‘a’=8，判断trie[2][8]=3，令p =3，沿第3个节点继续插入。

⑦ s[2]-‘a’=13，判断trie[3][13]为0，令trie[3][13]=6，end[6]=true。

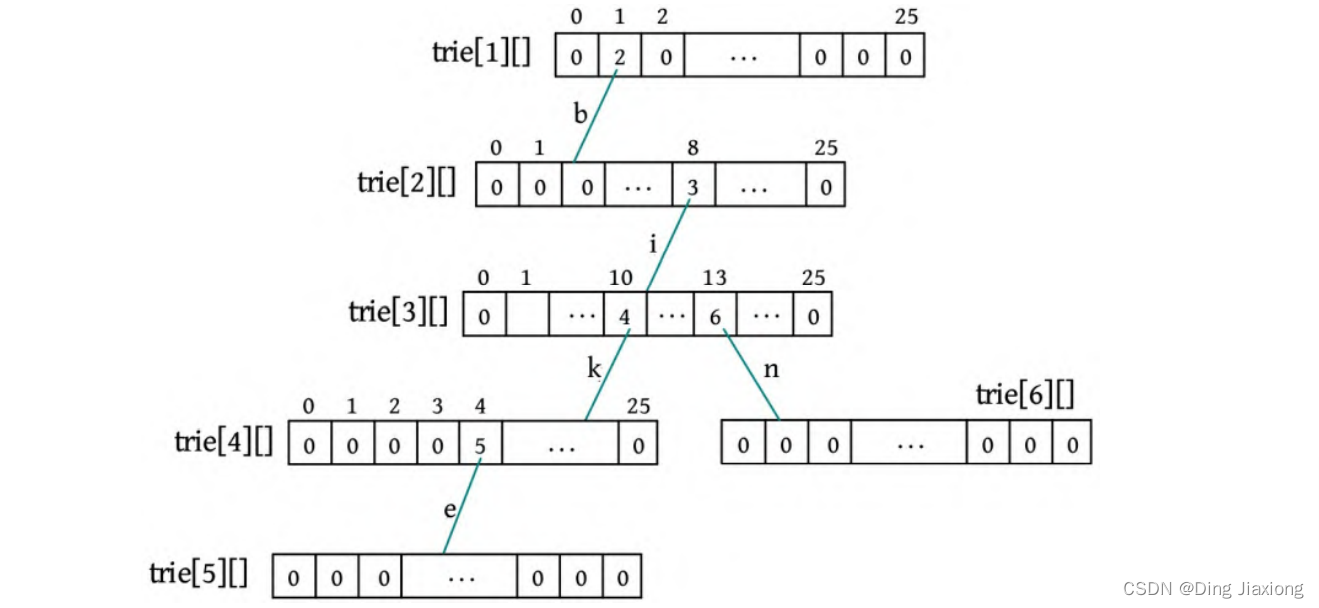
⑧ 接着插入一个单词s（yes），首先将字符转换为数字，s[0]-‘a’=24，判断trie[1][24]为0，令trie[1][24]=7。

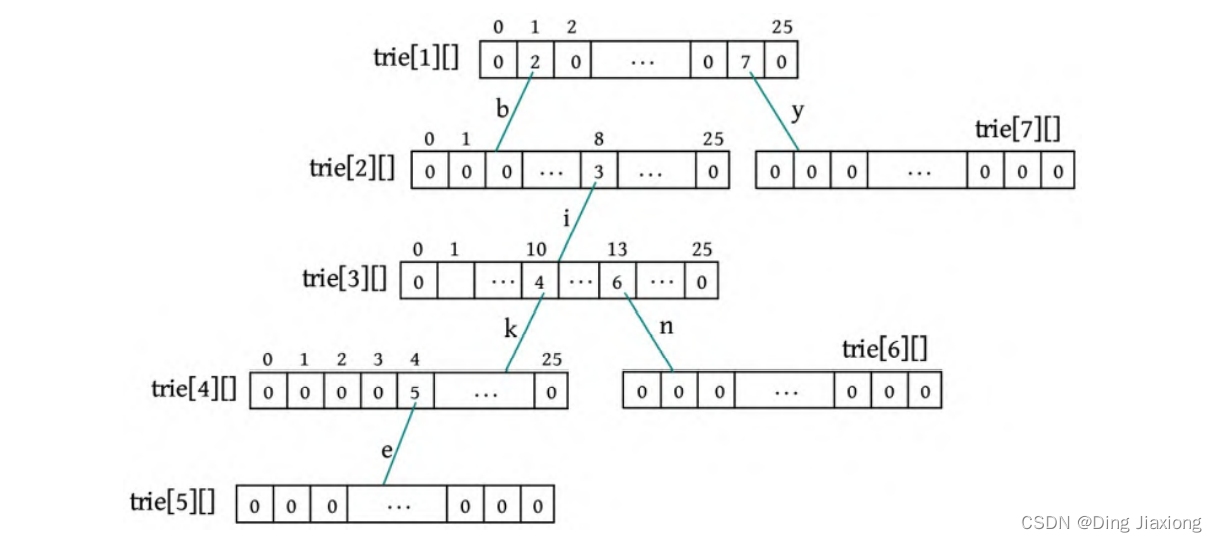
⑨ 继续插入s（yes）的后两个字符，end[9]=true，标记单词结束。

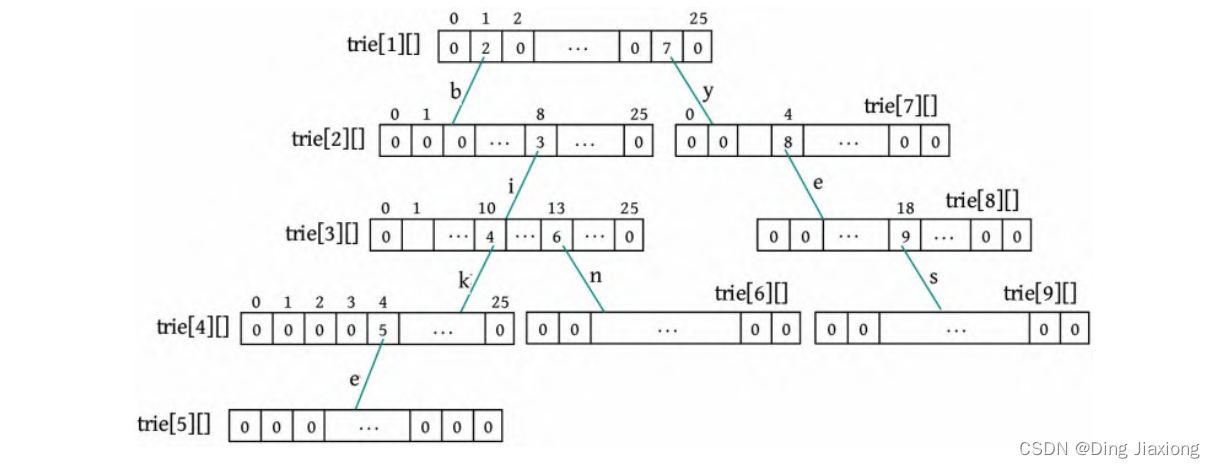
[算法代码]

void insert(string s){ // 将字符串s 插入字典树中
	
	int len = s.length() , p = 1;
	for(int i = 0 ; i < len ; i ++){
		
		int ch = s[i] - 'a';  //转换为数字
		if(!trie[p][ch]){
			trie[p][ch] = ++ tot;  //记录下标
		}
		p = trie[p][ch];
	}
	
	end[p] = true;  // 标记单词结束
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

[算法分析]

若单词的总长度为N ，字符的种类为k ，插入的字符串长度为n ，则创建Trie的复杂度为O (N )，空间复杂度为O (Nk )，插入字符串的时间复杂度均为O (n )。

【2】字典树的查找

若在字典树中查找该字符串是否存在，则和插入操作一样，首先将字符转换为数字，在字典树中查找，若查找的位置为0，则说明不存在，否则继续向下查找；在字符串处理完毕后，判断此处是否有单词结束标记，若有，则说明该字符串存在。

[ 举个栗子]

在字典树中查找单词s（bin）。

① 将字符转换为数字，s[0]-‘a’=1，判断trie[1][1]，若为0，则查找失败；trie[1][1]=2，不为0，则令p =2，在第2个节点继续查找。

② s[1]-‘a’=8，判断trie[2][8]，若为0，则查找失败；trie[2][8]=3，不为0，则令p =3，在第3个节点继续查找。

③ s[2]-‘a’=13，判断trie[3][13]，若为0，则查找失败；trie[3][13]=6，不为0，则令p =6，在第6个节点继续查找。

此时字符串处理完毕，看6号节点是否有单词结束标记，若end[6]为真，则返回查找成功，否则返回查找失败。

[算法代码]

bool search(string s){  //在字典树中查找该字符串是否存在
	int len = s.length() , p = 1;
	
	for(int i = 0 ; i < len ; i ++){
		p = trie[p][s[i] - 'a'];
		if(!p){
			return false;
		}
	}
	return end[p];
}
1
2
3
4
5
6
7
8
9
10
11

[算法分析]

在字典树中查找一个关键字的时间与树中包含的节点数无关，只与关键字的字符数有关。若查找的字符串长度为n ，则查找的时间复杂度均为O (n )。

【3】字典树的应用

① 字符串检索。事先将已知的一些字符串（字典）的有关信息存储到Trie树里，查找一些字符串是否出现过、出现的频率和搜索引擎的热门查询。

② 前缀统计。统计一个串所有前缀单词的个数，只需统计从根到叶子路径上单词出现的个数，也可以判断一个单词是否为另一个单词的前缀。

③ 最长公共前缀。Trie树利用多个字符串的公共前缀来节省存储空间，反之，当把大量字符串都存储到一棵Trie树上时，可以快速得到某些字符串的公共前缀。对所有字符串都建立字典树，两个串的最长公共前缀的长度就是它们所在节点最近公共祖先的长度，于是转变为最近公共祖先问题。

④ 排序。利用字典树进行串排序。例如，给定N 个互不相同的仅由一个单词构成的英文名，将它们按字典序从小到大输出。采用数组方式创建字典树，这棵树每个节点的所有子节点都按照其字母大小排序。对字典树进行先序遍历，输出的相应字符串便是按字典序排序的结果。

⑤ 作为其他数据结构与算法的辅助结构，例如后缀树、AC自动机等。