Python实现Stacking回归模型(随机森林回归、极端随机树回归、AdaBoost回归、GBDT回归、决策树回归)项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

Stacking通常考虑的是异质弱学习器（不同的学习算法被组合在一起），stacking学习用元模型组合基础模型。stacking 的概念是学习几个不同的弱学习器，并通过训练一个元模型来组合它们，然后基于这些弱模型返回的多个预测结果输出最终的预测结果。

本项目应用Stacking回归算法通过集成随机森林回归、极端随机森林回归、Adaboost回归、梯度提升树回归、决策树回归五个算法进行建模、预测及模型评估。

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

数据详情如下(部分展示)：

3.数据预处理

3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2 数据缺失查看

使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有10个变量，数据中无缺失值，共1000条数据。

关键代码：

3.3 数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

关键代码如下：

4.探索性数据分析

4.1 y变量直方图

用Matplotlib工具的hist()方法绘制直方图：

从上图可以看到，y变量主要集中在-200~200之间。

4.2 相关性分析

从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。  

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

5.2 数据集拆分

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下：

6.构建Stacking回归模型

主Stacking回归算法通过集成随机森林回归、极端随机森林回归、Adaboost回归、梯度提升树回归、决策树回归五个算法进行建模，用于目标回归。

6.1第一层模型参数

关键代码如下：

 6.2第一层模型特征重要性

 通过上图可以看出，随机森林模型特征重要性排名为x5、x6等。

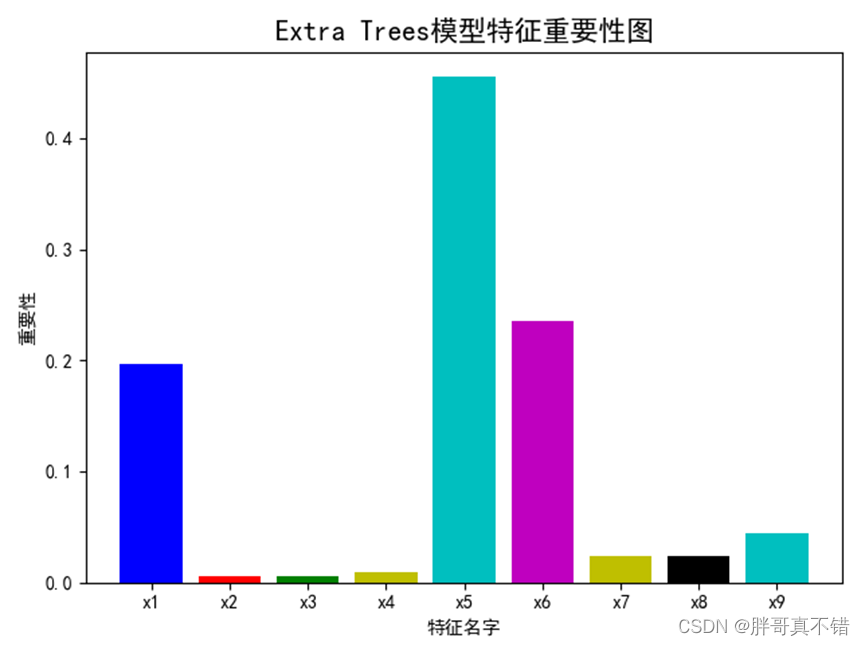
通过上图可以看出，极端随机树模型特征重要性排名为x5、x6等。

 通过上图可以看出，AdaBoost模型特征重要性排名为x5、x6等。

通过上图可以看出，Gradient Boost模型特征重要性排名为x5、x6等。 

通过上图可以看出，所有模型特征重要性排名为x5、x6、x1等。

6.3 五种模型相关性分析

针对五种模型的预测结果进行相关性分析，通过上图可以看出大于0的为正相关 数值越大相关性越强；小于0的为负相关。

6.4 第二层模型参数

关键代码如下：

7.模型评估

7.1 评估指标及结果

评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。

从上表可以看出，R方0.9707，为模型效果较好。

关键代码如下：

7.2 真实值与预测值对比图

从上图可以看出真实值和预测值波动基本一致，模型拟合效果良好。   

8.结论与展望

综上所述，本项目采用了应用Stacking回归算法通过集成随机森林回归、极端随机森林回归、Adaboost回归、梯度提升树回归、决策树回归五个算法进行建模及模型评估，最终证明了我们提出的模型效果较好。 

# 本次机器学习项目实战所需的资料，项目资源如下：
 
# 项目说明：
 
# 链接：https://pan.baidu.com/s/1VPWFSTp8cDrvLKYUYXiqvQ 
# 提取码：vqs0
 
# 用Pandas工具查看数据
print(df.head())
print('******************************')
 
# 数据缺失值统计
print(df.info())
print('******************************')
 
# 描述性统计分析
print(df.describe().round(4))
print('******************************')
 
# y变量分布直方图
fig = plt.figure(figsize=(8, 5))  # 设置画布大小
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
data_tmp = df['y']  # 过滤出y变量的样本
# 绘制直方图  bins：控制直方图中的区间个数 auto为自动填充个数  color：指定柱子的填充色
plt.hist(data_tmp, bins='auto', color='g')
plt.xlabel('y')
plt.ylabel('数量')