【leetcode】 盛最多水的容器

一、题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

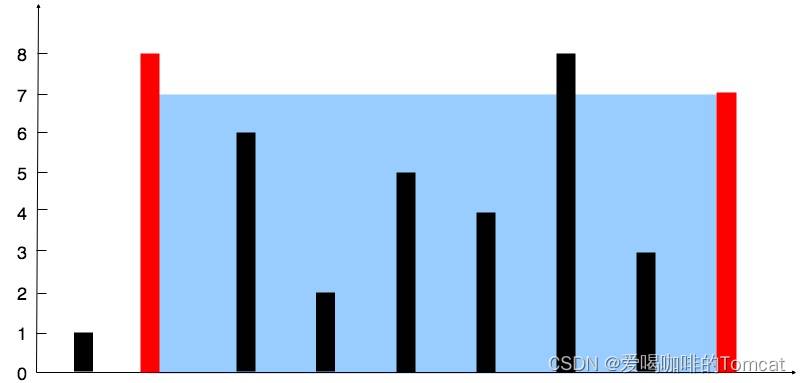
输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组
[1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

输入：height = [1,1] 输出：1

二、代码思路

分析题目，我们知道题目的意思是让我们求出两条棒子围出的最大面积，围出的面积是由短杆的高度乘与底边长得到的，也就是：

int area = (right - left) * Math.min(height[left], height[right]);

有两种解题方法

2.1 暴力题解

上面已经解释过了，目的是计算两条杠围成的最大面积，那么我们枚举出所有两条杠的组合即可。

2.2 双指针

上述的暴力题解，时间复杂度较高，题目要求n<10^5, on2的时间复杂度显然会超时的。所以想想优化的解法，题目中提到了左右两条杠组成的面积，所以我们可以考虑到双指针的解题思路。

但是问题的难点是双指针如何移动，我们考虑题目的要求，要求面积最大，面积是由左右杠高度以及左右杠之间的距离决定的，所以，移动规则如下：

• 如果left杠高度大于right杠那么移动right杠，也就是移动高度低的。
• 如果两条杠高度一致移动任意一个。
• 如果移动的时候发现相邻的杠高度比自身高度还低，那么不用计算其围成的面积。（因为底边长度度变少了，高度也变少了，那么面积必然也会变少）

那么如何证明我们移动的是正确的呢？

如果left杠高度大于right杠那么移动right杠，也就是移动高度低的。为什么移动高度低的？ 计算面积的时候是由高度低的决定的面积，如果不移动它，那么面积会一直受到其限制，这样造成的结果就是底边越来越短，高度不变，或者高度变得更低。所以，移动高度高的我们的面积只会越来越短，从而做一些没必要的计算，只有移动高度低的才有可能出现面积更大的元素。

考虑第一步，假设当前左指针和右指针指向的数分别为 x 和 y，不失一般性，我们假设 x≤y。同时，两个指针之间的距离为 t。那么，它们组成的容器的容量为：

min⁡(x,y)∗t=x∗t

我们可以断定，如果我们保持左指针的位置不变，那么无论右指针在哪里，这个容器的容量都不会超过 x∗tx * tx∗t 了。注意这里右指针只能向左移动，因为 我们考虑的是第一步，也就是 指针还指向数组的左右边界的时候。

详细题解：https://leetcode.cn/problems/container-with-most-water/solutions/207215/sheng-zui-duo-shui-de-rong-qi-by-leetcode-solution/

三、代码题解

package leetcode.lc20221204;

/*
 * @author lzy
 * @version 1.0
 * @DESC 乘最多水的容器
 * */
class Solution01 {
    public static void main(String[] args) {

    }
    //思路1 ：暴力解决
    //时间复杂度：o(n2) 2 <= n <= 10^5 会超时
    //空间复杂度：o1
    public int maxArea1(int[] height) {
        int res = 0;
        //边界值处理
        int length = height.length;
        if (length == 2) {
            return length * Math.min(height[0], height[1]);
        }
        //处理其他值,枚举出任意两根棒子组成的面积
        for (int i = 0; i < length; i++) {
            for (int j = i + 1; j < length; j++) {
                int area = (j - i) * Math.min(height[i],height[j]);
                res = area > res ? area : res;
            }
        }
        return res;
    }
    //思路2：双指针问题
    public int maxArea(int[] height) {
        int res = 0;
        //边界值处理
        int length = height.length;
        if (length == 2) {
            return length * Math.min(height[0], height[1]);
        }
        int left = 0;
        int right = length - 1;
        while (left < right) {
            int area = (right - left) * Math.min(height[left], height[right]);
            res = area > res ? area : res;
            if (height[left] > height[right]) {
                right--;
            } else {
                left++;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52