python练习题集锦之一

python练习题集锦之一

python练习题集锦之一，包括：1.限制输入的整数范围1到10之间、2.输出100以内素数（质数）及其和、3.求两个数最大公约数、最小公倍数

1.限制输入的整数范围1到10之间

源码如下：

提示 = '输入错误，请重新输入!'
while True:
    try:
        n = int(input('请输入一个正整数n(1≤n≤10)：'))
    except:
        print(Error)
        continue
    if 1<=n<=10:
        break
    else:
        print(提示)
 

2.输出100以内素数（质数）及其和

素数（质数）就是除了1和它本身外不存在任何因子的数。

素数（质数）算法

思路1)：因此判断一个整数m是否是素数，只需把 m 被 2 ~ m-1 之间的每一个整数去除，如果都不能被整除，那么 m 就是一个素数。

思路2)：另外判断方法还可以简化。m 不必被 2 ~ m-1 之间的每一个整数去除，只需被 2 ~  之间的每一个整数去除就可以了。如果 m 不能被 2 ~ 间任一整数整除，m 必定是素数。原因：因为如果 m 能被 2 ~ m-1 之间任一整数整除，其二个因子必定有一个小于或等于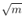，另一个大于或等于。例如 16 能被 2、4、8 整除，16=2*8，2 小于 4，8 大于 4，16=4*4，4=，因此只需判定在 2~4 之间有无因子即可。

思路一源码如下:

sum = 0
for i in range(2,100):
    for j in range(2,i):
        if (i%j == 0):            
            break
    else:
        print(i,end=" ")
        sum += i
 
print("和="+str(sum))
 

运行效果：

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 和=1060

思路二源码如下:

sum = 0
for i in range(2,100):
    for j in range(2,int(i ** 0.5)+1):  # 求根，向下取整再+1
        if (i%j == 0):            
            break
    else:
        print(i,end=" ")
        sum += i
 
print("和="+str(sum))

3. 求两个数最大公约数、最小公倍数

辗转相除法求最大公约数算法：

① 整数A对整数B进行取整, 余数用整数C来表示    举例: C = A % B

② 如果C等于0,则C就是整数A和整数B的最大公约数

③ 如果C不等于0, 将B赋值给A, 将C赋值给B ,然后进行 1, 2 两步,直到余数为0, 则可以得知最大公约数

最小公倍数  =  两个整数的乘积 /  最大公约数

源码如下：

#辗转相除法求两个数的最大公约(GreatestCommonDivisor)
def GCD(a, b):
    # 如果最终余数为0 公约数就计算出来了
    while(b!=0):
        temp = a % b
        a = b
        b = temp
    return a
 
# 求两个数的最小公倍数(LeastCommonMultiple)
def LCM(a,b):
    return a * b / GCD(a, b)
 
print("最大公约数为:%d" % GCD(6,9))  # 输出  
 
print("最小公倍数:%d" % LCM(6,9))  # 输出

运行效果：

最大公约数为:3
最小公倍数:18

OK！