1552. 两球之间的磁力-快速排序+二分查找

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i] ，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力 最大。

已知两个球如果分别位于 x 和 y ，那么它们之间的磁力为 |x - y| 。

给你一个整数数组 position 和一个整数 m ，请你返回最大化的最小磁力。

示例 1：

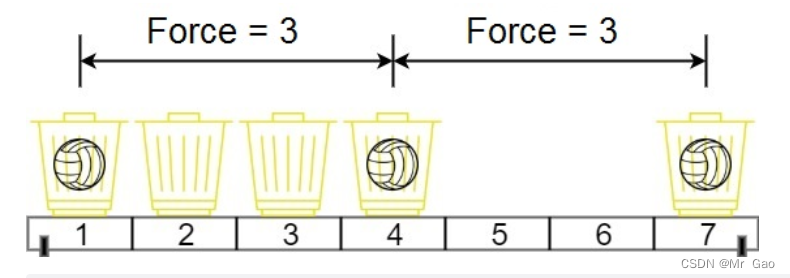
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例 2：

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

这个题目也是非常帮哈，对于这个题目，一开始的时候，博主想的时快速排序+动态规划，事实上，博主写动态规划写到一半的时候，突然就意识到，动态规划时间复杂度不能通过，所以想到了二分查找，这个算法思路很棒，感兴趣的学习一下，解题代码如下：

void quick(int *a,int low,int high){
    if(low<high){
        int l=low,h=high,p=a[low];
        while(low<high){
            while(low<high&&a[high]>=p){
                high--;

            }
            a[low]=a[high];
            while(low<high&&a[low]<=p){
                low++;
            }
            a[high]=a[low];
        }
        a[low]=p;
        quick(a,l,low-1);
        quick(a,low+1,h);
    }
}


bool  judge(int threshold,int* position, int positionSize, int m){
    
    int count=1;
    int pre_index=0;
    for(int i=1;i<positionSize;i++){
        if(position[i]-position[pre_index]>=threshold){
            count++;
            pre_index=i;

        }
         if(count>=m){
        return true;
    }

    }
   return false;
}

int maxDistance(int* position, int positionSize, int m){
    quick(position,0,positionSize-1);
    int min=1,max=position[positionSize-1];
    while(min<=max){
        int mid=(max+min)/2;
        if(judge(mid,position,positionSize,m)){
            min=mid+1;
        }
        else{
            max=mid-1;
        }
    }
    return min-1;
   



}








1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65