-
图的初识·遍历
深度优先搜索[DFS]
- 并不唯一,只是一种情况
A
−
>
I
A->I
A−>I

实现代码

- 使用邻接表表示图。遍历的时间复杂度 O ( V + E ) O(V+E) O(V+E);邻接矩阵的时间复杂度为 O ( V 2 ) O(V^2) O(V2)
#include#include #define MaxVertex 5 typedef char E; //结点和头节点分开定义,普通结点记录邻接顶点信息 typedef struct node { int nextVertex; struct node *next; } *Node; //头节点记录元素 struct HeadNode { E element; struct node * next; }; typedef struct AdjacencyGraph { int vertexCount;//顶点数 int edgeCount;//边数 struct HeadNode vertex[MaxVertex]; }* Graph; //初始化 Graph create(); //添加顶点 void addVertex(Graph graph,E element); //添加边的关系 void addEdge(Graph graph,int a,int b); //打印邻接表 void printGraph(Graph graph); //深度优先搜索算法 int dfs(Graph graph,int startVertex,int targetVertex,int* visited); - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
#include "Map2.h" //创建 Graph create() { Graph graph=(Graph) malloc(sizeof(struct AdjacencyGraph)); graph->vertexCount=graph->edgeCount=0; return graph; }; //添加顶点 void addVertex(Graph graph,E element) { if(graph->vertexCount>=MaxVertex) return; //添加新节点 graph->vertex[graph->vertexCount].element=element; graph->vertex[graph->vertexCount].next=NULL; graph->vertexCount++;//顶点数更新 } void addEdge(Graph graph,int a,int b) { //定义一个指向链表的头结点的下一结点指向 Node node=graph->vertex[a].next; //开辟顶点空间 Node newNode=(Node) malloc(sizeof(struct node)); newNode->next=NULL; newNode->nextVertex=b; //如果头结点下面没有东西,就直接连接;否则,就遍历到最后一个结点后,添加新节点 if(!node) { graph->vertex[a].next=newNode;//注意这里不能使用node,因为我们要真实地改变头节点的next指向 }else { do{ //如果已经连接到对应的结点,直接返回 if(node->nextVertex==b) { free(newNode); newNode=NULL; return ; } //否则一直遍历到最后一个结点 if(node->next) node=node->next; else break;//如果遭到了最后一个结点,直接结束 }while(true); node->next=newNode; } graph->edgeCount++;//边数计数+1 } //打印 void printGraph(Graph graph) { for(int i=0;i<graph->vertexCount;i++) { printf("%d | %c",i,graph->vertex[i].element); Node node=graph->vertex[i].next; while(node) { printf("-> %d",node->nextVertex); node=node->next; } printf("\n"); } } /** * 深度优先搜索算法 * @param graph 图 * @param startVertex 起点顶点下标 * @param targetVertex 目标顶点下标 * @param visited 已到达过的顶点数组 */ int dfs(Graph graph,int startVertex,int targetVertex,int* visited) { visited[startVertex]=1;//标记访问过的结点 //大一当前结点 printf("%c->",graph->vertex[startVertex].element); //如果当前顶点就是要找的顶点,就直接返回 if(startVertex==targetVertex) return 1; //遍历当前顶点所有的分支 Node node=graph->vertex[startVertex].next; while(node) { //如果已经到过[做的其他分支、回头路],就停止 if(!visited[node->nextVertex]) { //没到过就继续往下走 //如果查找成功就返回一,不用再看其他分支。 if(dfs(graph,node->nextVertex,targetVertex,visited)) { return 1; } } node=node->next; } return 0;//当下的遍历都结束后,还是没有找到就返回零 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
#include "Map2.h" int main() { Graph graph1 = create(); for (int c = 'A'; c <= 'F'; c++) { addVertex(graph1, (char) c); } addEdge(graph1, 0, 1);//A->B addEdge(graph1, 1, 2);//B->C addEdge(graph1, 1, 3);//B->D addEdge(graph1, 1, 4);//D->E //addEdge(graph1, 4, 5);//E->F printGraph(graph1); int arr[graph1->vertexCount]; for(int i=0;i<graph1->vertexCount;i++) { arr[i]=0; } printf("\n%d",dfs(graph1,0,5,arr)); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21

广度优先搜索【BFS】
- 先探索顶点的所有分支,然后再去看这些分支的所有分支。
- 实质上是更尽可能地探索更广的范围。
思路图解
从 A 结 点 开 始 探 索 , A 入 队 列 。 队 列 状 态 : A 然 后 , 再 将 其 下 一 个 结 点 B 入 队 , A 出 队 。 队 列 状 态 : B 从A结点开始探索,A入队列。\\ 队列状态:A\\ 然后,再将其下一个结点B入队,A出队。\\ 队列状态:B\\ 从A结点开始探索,A入队列。队列状态:A然后,再将其下一个结点B入队,A出队。队列状态:B
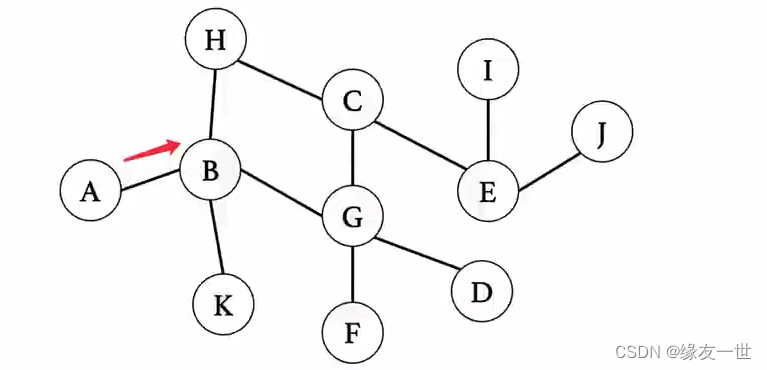
将 B 的 下 一 级 结 点 入 队 队 列 状 态 : B − > H − > G − > K 将 B 出 队 队 列 状 态 : H − > G − > K 将B的下一级结点入队\\ 队列状态:B->H->G->K\\ 将B出队\\ 队列状态:H->G->K 将B的下一级结点入队队列状态:B−>H−>G−>K将B出队队列状态:H−>G−>K
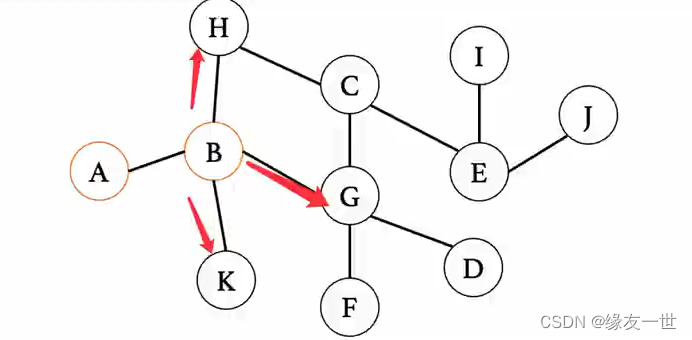
依 次 按 照 队 头 到 队 尾 的 顺 序 , 将 其 子 节 点 入 队 , 本 结 点 出 队 。 C 入 队 队 列 状 态 : H − > G − > K − > C H 出 队 对 列 状 态 : G − > K − > C 依次按照队头到队尾的顺序,将其子节点入队,本结点出队。\\ C入队\\ 队列状态:H->G->K->C\\ H出队\\ 对列状态:G->K->C 依次按照队头到队尾的顺序,将其子节点入队,本结点出队。C入队队列状态:H−>G−>K−>CH出队对列状态:G−>K−>C

D 、 F 入 队 ; C 已 入 队 , 所 以 无 需 再 次 入 队 。 队 列 状 态 : G − > K − > C − > D − > F G 出 队 对 列 状 态 : K − > C − > D − > F D、F入队;C已入队,所以无需再次入队。\\ 队列状态:G->K->C->D->F\\ G出队\\ 对列状态:K->C->D->F\\ D、F入队;C已入队,所以无需再次入队。队列状态:G−>K−>C−>D−>FG出队对列状态:K−>C−>D−>F

K 没 有 下 一 个 结 点 , 所 以 直 接 将 K 出 队 。 队 列 状 态 : C − > D − > F K没有下一个结点,所以直接将K出队。\\ 队列状态:C->D->F K没有下一个结点,所以直接将K出队。队列状态:C−>D−>F

再 依 次 遍 历 队 头 的 下 一 个 结 点 E 入 队 队 列 状 态 : C − > D − > F − > E C 出 队 队 列 状 态 : D − > F − > E 再依次遍历队头的下一个结点\\ E入队\\ 队列状态:C->D->F->E C出队\\ 队列状态:D->F->E 再依次遍历队头的下一个结点E入队队列状态:C−>D−>F−>EC出队队列状态:D−>F−>E
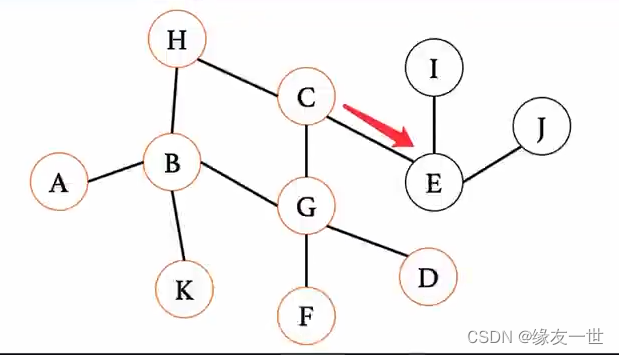
因 为 D 、 F 没 有 下 一 级 邻 接 点 , 所 以 将 D 、 F 出 队 即 可 队 列 状 态 : E 因为D、F没有下一级邻接点,所以将D、F出队即可\\ 队列状态:E 因为D、F没有下一级邻接点,所以将D、F出队即可队列状态:E
I 、 J 入 队 队 列 状 态 : E − > I − > J E 出 队 队 列 状 态 : I − > J I、J入队\\ 队列状态:E->I->J E出队\\ 队列状态:I->J I、J入队队列状态:E−>I−>JE出队队列状态:I−>J

最 后 再 将 队 列 的 内 容 全 部 出 队 队 列 状 态 : 空 结 束 搜 索 最后再将队列的内容全部出队\\ 队列状态:空\\ 结束搜索 最后再将队列的内容全部出队队列状态:空结束搜索代码实现·广度优先遍历【BFS】
- 存储结构:邻接表
图的结构
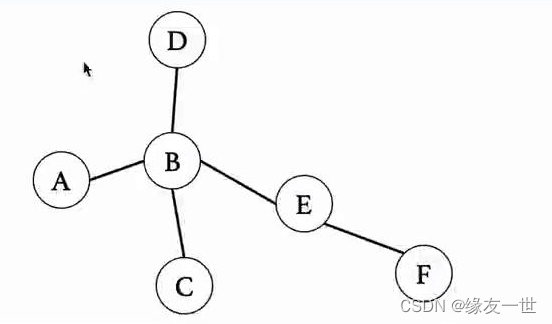
typedef int T; struct QueueNode{ T element; struct QueueNode * next; }; typedef struct QueueNode* QNode; struct Queue{ QNode front,rear; }; typedef struct Queue* LinkedQueue; int initQueue(LinkedQueue queue) { QNode node=(QNode) malloc(sizeof(struct QueueNode)); if(node==NULL) return 0; queue->front=queue->rear=node; return 1; } int offerQueue(LinkedQueue queue,T element) { QNode node=(QNode) malloc(sizeof(struct QueueNode)); if(node== NULL) return 0; node->element=element; queue->rear->next=node; queue->rear=node; return 1; } int isEmpty(LinkedQueue queue){ return queue->front==queue->rear; }; T pollQueue(LinkedQueue queue) { T e=queue->front->next->element; QNode node=queue->front->next; queue->front->next=queue->front->next->next; if(queue->rear==node) queue->rear=queue->front; free(node); return e; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- BFS
/** * * @param graph 图 * @param startVertex 起点顶点下标 * @param targetVertex 目标顶点下标 * @param visited 已到达过的顶点数组 * @param queue 辅助作用的队列 * @return */ int bfs(Graph graph,int startVertex,int targetVertex,int* visited,LinkedQueue queue) { offerQueue(queue,startVertex);//头节点入队 visited[startVertex]=1;//立马已标记 //当队列不为空时,进行操作 while(!isEmpty(queue)) { int next= pollQueue(queue);//从队列中取出一个顶点打印 printf("%c->",graph->vertex[next].element); Node node=graph->vertex[next].next;//下一个结点 //当当前结点的下一个结点存在时,进行入队操作 while(node) { //如果找到目标结点,返回true if(node->nextVertex==targetVertex) return true; if(!visited[node->nextVertex]) {//!0==1未访问 offerQueue(queue,node->nextVertex);//入队列 visited[node->nextVertex]=1;//访问标记 } node=node->next;//进行下一个结点 } } return false; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Main.cpp
Graph graph1 = create(); for (int c = 'A'; c <= 'F'; c++) { addVertex(graph1, (char) c); } addEdge(graph1, 0, 1);//A->B addEdge(graph1, 1, 2);//B->C addEdge(graph1, 1, 3);//B->D addEdge(graph1, 1, 4);//D->E addEdge(graph1, 4, 5);//E->F printGraph(graph1); int arr1[graph1->vertexCount]; for(int i=0;i<graph1->vertexCount;i++) { arr1[i]=0; } struct Queue queue; initQueue(&queue); bfs(graph1,0,5,arr1,&queue);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17

- 并不唯一,只是一种情况
A
−
>
I
A->I
A−>I
-
相关阅读:
【python学习】-matplotlib绘制双坐标柱状图
php8.2 安装swoole扩展 (mac m1)
【云原生·k8s】k8s集群安装部署
系统编程 day10 管道的知识 (无名管道 ,有名管道 ,管道通信,管道的函数,管道的知识(什么是管道 ,,,) )
Nginx简介,Nginx搭载负载均衡以及Nginx部署前端项目
深度学习模型部署全流程-模型部署
金蝶云星空简单账表动态列名汇总
CRM项目记录(七)
疯狂星期四的营销策略是什么?如何复制?
Codeforces Round #809 (Div. 2) A~D
- 原文地址:https://blog.csdn.net/yang2330648064/article/details/128124273
