• NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验

    文章目录

    6.3 LSTM的记忆能力实验

    长短期记忆网络（Long Short-Term Memory Network，LSTM）是一种可以有效缓解长程依赖问题的循环神经网络．LSTM 的特点是引入了一个新的内部状态（Internal State）c∈RD 和门控机制（Gating Mechanism）．不同时刻的内部状态以近似线性的方式进行传递，从而缓解梯度消失或梯度爆炸问题．同时门控机制进行信息筛选，可以有效地增加记忆能力．
    使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。
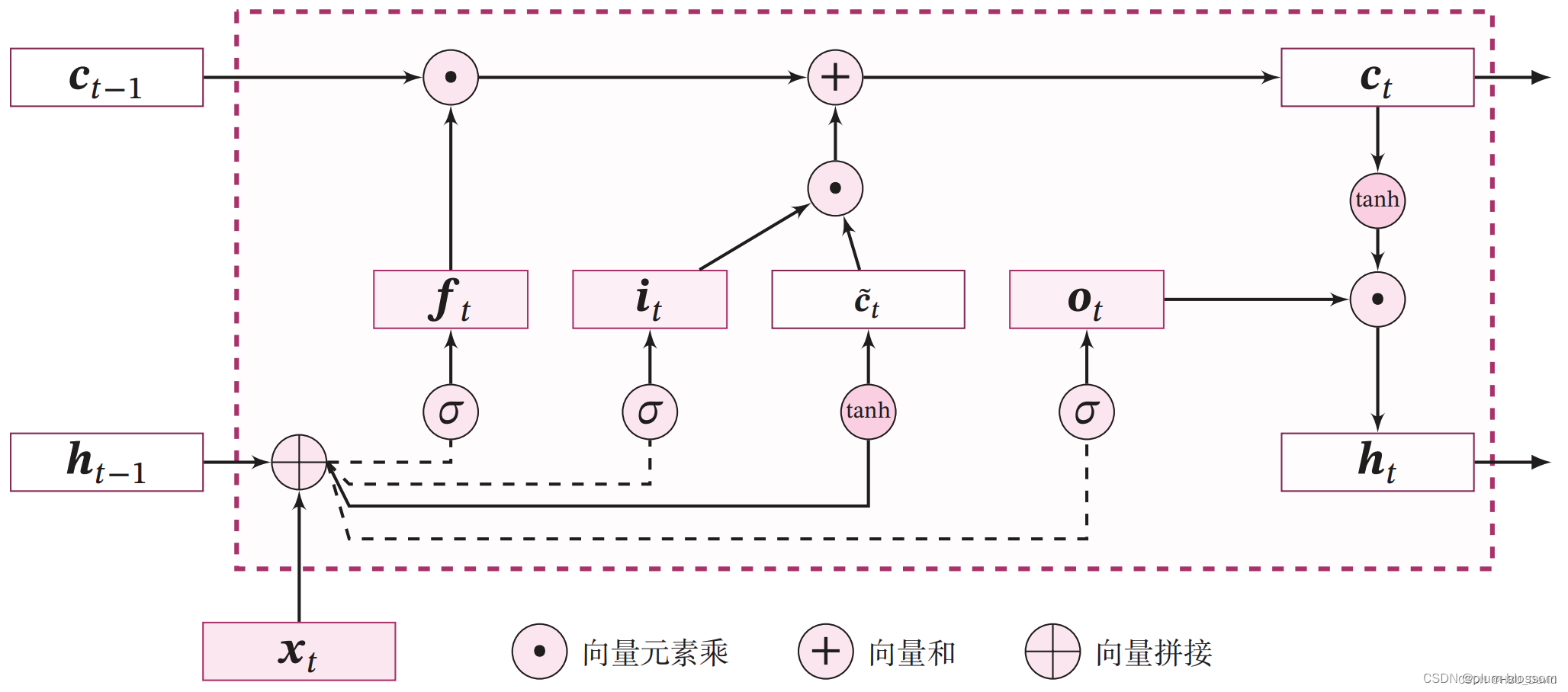
    在这里插入图片描述

    6.3.1 模型构建

    使用第6.1.2.4节中定义Model_RNN4SeqClass模型，并构建 LSTM 算子．

    只需要实例化 LSTM ，并传入Model_RNN4SeqClass模型，就可以用 LSTM 进行数字求和实验。

    6.3.1.1 LSTM层

    自定义LSTM算子
    nn.LSTM
    将自定义LSTM与pytorch内置的LSTM进行对比
    LSTM层的代码与SRN层结构相似，只是在SRN层的基础上增加了内部状态、输入门、遗忘门和输出门的定义和计算。这里LSTM层的输出也依然为序列的最后一个位置的隐状态向量。代码实现如下：

    class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, Wi_attr=None, Wf_attr=None, Wo_attr=None, Wc_attr=None,
                 Ui_attr=None, Uf_attr=None, Uo_attr=None, Uc_attr=None, bi_attr=None, bf_attr=None,
                 bo_attr=None, bc_attr=None):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size



        W_i = torch.randn([input_size, hidden_size])
        W_f = torch.randn([input_size, hidden_size])
        W_o = torch.randn([input_size, hidden_size])
        W_c = torch.randn([input_size, hidden_size])
        U_i = torch.randn([hidden_size, hidden_size])
        U_f = torch.randn([hidden_size, hidden_size])
        U_o = torch.randn([hidden_size, hidden_size])
        U_c = torch.randn([hidden_size, hidden_size])
        b_i = torch.randn([1, hidden_size])
        b_f = torch.randn([1, hidden_size])
        b_o = torch.randn([1, hidden_size])
        b_c = torch.randn([1, hidden_size])
        self.W_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_i, dtype=torch.float32), gain=1.0))
        # 初始化模型参数
        self.W_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_f, dtype=torch.float32), gain=1.0))
        self.W_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_o, dtype=torch.float32), gain=1.0))
        self.W_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_c, dtype=torch.float32), gain=1.0))
        self.U_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_i, dtype=torch.float32), gain=1.0))
        self.U_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_f, dtype=torch.float32), gain=1.0))
        self.U_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_o, dtype=torch.float32), gain=1.0))
        self.U_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_c, dtype=torch.float32), gain=1.0))
        self.b_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_i, dtype=torch.float32), gain=1.0))
        self.b_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_f, dtype=torch.float32), gain=1.0))
        self.b_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_o, dtype=torch.float32), gain=1.0))
        self.b_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_c, dtype=torch.float32), gain=1.0))

    # 初始化状态向量和隐状态向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros([batch_size, self.hidden_size])
        cell_state = torch.zeros([batch_size, self.hidden_size])
        return hidden_state, cell_state

    # 定义前向计算
    def forward(self, inputs, states=None):
        # inputs: 输入数据，其shape为batch_size x seq_len x input_size
        batch_size, seq_len, input_size = inputs.shape

        # 初始化起始的单元状态和隐状态向量，其shape为batch_size x hidden_size
        if states is None:
            states = self.init_state(batch_size)
        hidden_state, cell_state = states

        # 执行LSTM计算，包括：输入门、遗忘门和输出门、候选内部状态、内部状态和隐状态向量
        for step in range(seq_len):
            # 获取当前时刻的输入数据step_input: 其shape为batch_size x input_size
            step_input = inputs[:, step, :]
            # 计算输入门, 遗忘门和输出门, 其shape为：batch_size x hidden_size
            I_gate = F.sigmoid(torch.matmul(step_input, self.W_i) + torch.matmul(hidden_state, self.U_i) + self.b_i)
            F_gate = F.sigmoid(torch.matmul(step_input, self.W_f) + torch.matmul(hidden_state, self.U_f) + self.b_f)
            O_gate = F.sigmoid(torch.matmul(step_input, self.W_o) + torch.matmul(hidden_state, self.U_o) + self.b_o)
            # 计算候选状态向量, 其shape为：batch_size x hidden_size
            C_tilde = F.tanh(torch.matmul(step_input, self.W_c) + torch.matmul(hidden_state, self.U_c) + self.b_c)
            # 计算单元状态向量, 其shape为：batch_size x hidden_size
            cell_state = F_gate * cell_state + I_gate * C_tilde
            # 计算隐状态向量，其shape为：batch_size x hidden_size
            hidden_state = O_gate * F.tanh(cell_state)

        return hidden_state
Wi_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wf_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wo_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wc_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Ui_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uf_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uo_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uc_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
bi_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bf_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bo_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bc_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))

lstm = LSTM(2, 2, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)

inputs = torch.tensor([[[1, 0]]], dtype=torch.float32)
hidden_state = lstm(inputs)
print(hidden_state)


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89

    运行结果：
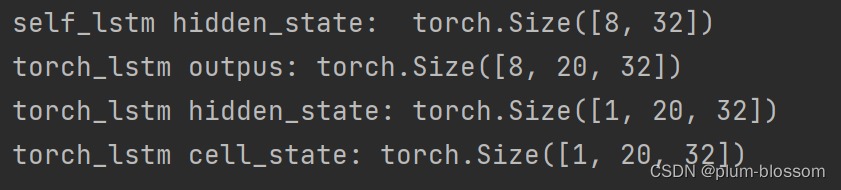
    在这里插入图片描述
    将自己实现的SRN和Torch框架内置的SRN返回的结果进行打印展示：

    # 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn([batch_size, seq_len, input_size])

# 设置模型的hidden_size
hidden_size = 32
torch_lstm = nn.LSTM(input_size, hidden_size)
self_lstm = LSTM(input_size, hidden_size)

self_hidden_state = self_lstm(inputs)
torch_outputs, (torch_hidden_state, torch_cell_state) = torch_lstm(inputs)

print("self_lstm hidden_state: ", self_hidden_state.shape)
print("torch_lstm outpus:", torch_outputs.shape)
print("torch_lstm hidden_state:", torch_hidden_state.shape)
print("torch_lstm cell_state:", torch_cell_state.shape)

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16

    运行结果：
    在这里插入图片描述
    定义输入数据inputs，然后将该数据分别传入Torch内置的LSTM与自己实现的LSTM模型中，最后通过对比两者的隐状态输出向量：

    import torch
torch.manual_seed(0)

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size, hidden_size = 2, 5, 10, 10
inputs = torch.randn([batch_size, seq_len, input_size])

# 设置模型的hidden_size
# bih_attr = torch.nn.Parameter(torch.tensor(torch.zeros([4*hidden_size, ])))
torch_lstm = nn.LSTM(input_size, hidden_size, bias=True)

# 获取torch_lstm中的参数，并设置相应的paramAttr,用于初始化lstm
print(torch_lstm.weight_ih_l0.T.shape)
chunked_W = torch.split(torch_lstm.weight_ih_l0.T, 4, dim=-1)
chunked_U = torch.split(torch_lstm.weight_hh_l0.T, 4, dim=-1)
chunked_b = torch.split(torch_lstm.bias_hh_l0.T, 4, dim=-1)

Wi_attr = torch.nn.Parameter(torch.tensor(chunked_W[0].clone().detach().requires_grad_(True)))
Wf_attr = torch.nn.Parameter(torch.tensor(chunked_W[1].clone().detach().requires_grad_(True)))
Wc_attr = torch.nn.Parameter(torch.tensor(chunked_W[2].clone().detach().requires_grad_(True)))
Wo_attr = torch.nn.Parameter(torch.tensor(chunked_W[3].clone().detach().requires_grad_(True)))
Ui_attr = torch.nn.Parameter(torch.tensor(chunked_U[0].clone().detach().requires_grad_(True)))
Uf_attr = torch.nn.Parameter(torch.tensor(chunked_U[1].clone().detach().requires_grad_(True)))
Uc_attr = torch.nn.Parameter(torch.tensor(chunked_U[2].clone().detach().requires_grad_(True)))
Uo_attr = torch.nn.Parameter(torch.tensor(chunked_U[3].clone().detach().requires_grad_(True)))
bi_attr = torch.nn.Parameter(torch.tensor(chunked_b[0].clone().detach().requires_grad_(True)))
bf_attr = torch.nn.Parameter(torch.tensor(chunked_b[1].clone().detach().requires_grad_(True)))
bc_attr = torch.nn.Parameter(torch.tensor(chunked_b[2].clone().detach().requires_grad_(True)))
bo_attr = torch.nn.Parameter(torch.tensor(chunked_b[3].clone().detach().requires_grad_(True)))
self_lstm = LSTM(input_size, hidden_size, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)

# 进行前向计算，获取隐状态向量，并打印展示
self_hidden_state = self_lstm(inputs)
torch_outputs, (torch_hidden_state, _) = torch_lstm(inputs)
print("torch SRN:\n", torch_hidden_state.detach().numpy().squeeze(0))
print("self SRN:\n", self_hidden_state.detach().numpy())

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38

    运行结果：
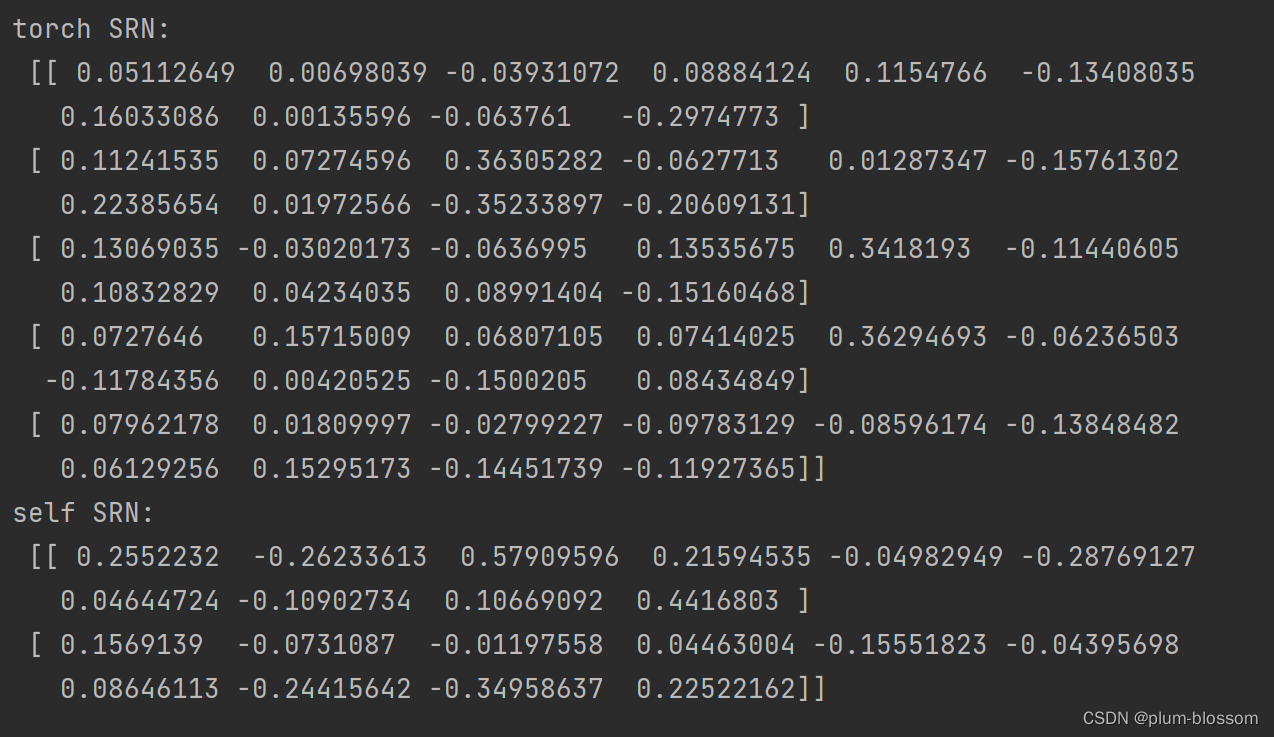
    在这里插入图片描述
    可以看到，两者的输出基本是一致的。另外，还可以进行对比两者在运算速度方面的差异。代码实现如下：

    import time

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn([batch_size, seq_len, input_size])

# 设置模型的hidden_size
hidden_size = 32
self_lstm = LSTM(input_size, hidden_size)
torch_lstm = nn.LSTM(input_size, hidden_size)

# 计算自己实现的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    hidden_state = self_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('self_lstm speed:', avg_model_time, 's')

# 计算torch内置的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    outputs, (hidden_state, cell_state) = torch_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('torch_lstm speed:', avg_model_time, 's')

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36

    运行结果：
    在这里插入图片描述
    可以看到，由于PyTorch底层采用了C++实现并进行优化，Paddle框架内置的LSTM运行效率远远高于自己实现的LSTM。

    6.3.1.2 模型汇总
    # 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
    def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
        super(Model_RNN4SeqClass, self).__init__()
        # 传入实例化的RNN层，例如SRN
        self.rnn_model = model
        # 词典大小
        self.num_digits = num_digits
        # 嵌入向量的维度
        self.input_size = input_size
        # 定义Embedding层
        self.embedding = Embedding(num_digits, input_size)
        # 定义线性层
        self.linear = nn.Linear(hidden_size, num_classes)

    def forward(self, inputs):
        # 将数字序列映射为相应向量
        inputs_emb = self.embedding(inputs)
        # 调用RNN模型
        hidden_state = self.rnn_model(inputs_emb)
        # 使用最后一个时刻的状态进行数字预测
        logits = self.linear(hidden_state)
        return logits

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23

    6.3.2 模型训练

    6.3.2.1 训练指定长度的数字预测模型

    本节将基于RunnerV3类进行训练，首先定义模型训练的超参数，并保证和简单循环网络的超参数一致. 然后定义一个train函数，其可以通过指定长度的数据集，并进行训练. 在train函数中，首先加载长度为length的数据，然后实例化各项组件并创建对应的Runner，然后训练该Runner。同时在本节将使用4.5.4节定义的准确度（Accuracy）作为评估指标，代码实现如下：

    import os
import random
import torch
import numpy as np

# 训练轮次
num_epochs = 500
# 学习率
lr = 0.001
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 8
# 模型保存目录
save_dir = "./checkpoints"

# 可以设置不同的length进行不同长度数据的预测实验
def train(length):
    print(f"\n====> Training LSTM with data of length {length}.")
    np.random.seed(0)
    random.seed(0)
    torch.manual_seed(0)

    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples), DigitSumDataset(test_examples)
    train_loader = DataLoader(train_set, batch_size=batch_size)
    dev_loader = DataLoader(dev_set, batch_size=batch_size)
    test_loader = DataLoader(test_set, batch_size=batch_size)
    # 实例化模型
    base_model = LSTM(input_size, hidden_size)
    model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
    # 指定优化器
    optimizer = torch.optim.Adam(model.parameters(),lr)
    # 定义评价指标
    metric = Accuracy()
    # 定义损失函数
    loss_fn = torch.nn.CrossEntropyLoss()
    # 基于以上组件，实例化Runner
    runner = RunnerV3(model, optimizer, loss_fn, metric)

    # 进行模型训练
    model_save_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
    runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=100, save_path=model_save_path)

    return runner

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53

    RunnerV3:

    class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric  # 只用于计算评价指标

        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []

        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = []  # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []

        # 记录全局最优指标
        self.best_score = 0

    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)

        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        custom_print_log = kwargs.get("custom_print_log", None)

        # 训练总的步数
        num_training_steps = num_epochs * len(train_loader)

        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')

        # 运行的step数目
        global_step = 0

        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                y = torch.tensor(y, dtype=torch.int64)
                loss = self.loss_fn(logits, y)  # 默认求mean
                total_loss += loss

                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step, loss.item()))

                if log_steps and global_step % log_steps == 0:
                    print(
                        f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")

                # 梯度反向传播，计算每个参数的梯度值
                loss.backward()
                torch.nn.utils.clip_grad_norm_(parameters=self.model.parameters(), max_norm=5, norm_type=1)
                if custom_print_log:
                    custom_print_log(self)

                # 小批量梯度下降进行参数更新
                self.optimizer.step()
                # 梯度归零
                self.optimizer.zero_grad()

                # 判断是否需要评价
                if eval_steps > 0 and global_step > 0 and \
                        (global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):

                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")

                    # 将模型切换为训练模式
                    self.model.train()

                    # 如果当前指标为最优指标，保存该模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(
                            f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score

                global_step += 1

            # 当前epoch 训练loss累计值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)

        print("[Train] Training done!")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None

        # 将模型设置为评估模式
        self.model.eval()

        global_step = kwargs.get("global_step", -1)

        # 用于统计训练集的损失
        total_loss = 0

        # 重置评价
        self.metric.reset()

        # 遍历验证集每个批次
        for batch_id, data in enumerate(dev_loader):
            X, y = data

            # 计算模型输出
            logits = self.model(X)
            y = y.clone().detach()

            # 计算损失函数
            loss = self.loss_fn(logits, y).item()
            # 累积损失
            total_loss += loss

            # 累积评价
            self.metric.update(logits, y)

        dev_loss = (total_loss / len(dev_loader))
        dev_score = self.metric.accumulate()

        # 记录验证集loss
        if global_step != -1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)

        return dev_score, dev_loss

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits

    def save_model(self, save_path):
        torch.save(self.model.state_dict(), save_path)

    def load_model(self, model_path):
        model_state_dict = torch.load(model_path)
        self.model.state_dict(model_state_dict)

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159

    Accuracy:

    class Accuracy():
    def __init__(self, is_logist=True):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """

        # 用于统计正确的样本个数
        self.num_correct = 0
        # 用于统计样本的总数
        self.num_count = 0

        self.is_logist = is_logist

    def update(self, outputs, labels):
        """
        输入：
           - outputs: 预测值, shape=[N,class_num]
           - labels: 标签值, shape=[N,1]
        """

        # 判断是二分类任务还是多分类任务，shape[1]=1时为二分类任务，shape[1]>1时为多分类任务
        if outputs.shape[1] == 1:  # 二分类
            outputs = torch.squeeze(outputs, dim=-1)
            if self.is_logist:
                # logist判断是否大于0
                preds = torch.tensor((outputs >= 0), dtype=torch.float32)
            else:
                # 如果不是logist，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
                preds = torch.tensor((outputs >= 0.5), dtype=torch.float32)
        else:
            # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
            preds = torch.argmax(outputs, dim=1)
            preds = preds.clone().detach()

        # 获取本批数据中预测正确的样本个数
        labels = torch.squeeze(labels, dim=-1)
        batch_correct = torch.sum((preds == labels).clone().detach()).numpy()
        batch_count = len(labels)

        # 更新num_correct 和 num_count
        self.num_correct += batch_correct
        self.num_count += batch_count

    def accumulate(self):
        # 使用累计的数据，计算总的指标
        if self.num_count == 0:
            return 0
        return self.num_correct / self.num_count

    def reset(self):
        # 重置正确的数目和总数
        self.num_correct = 0
        self.num_count = 0

    def name(self):
        return "Accuracy"

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    6.3.2.2 多组训练

    接下来，分别进行数据长度为10, 15, 20, 25, 30, 35的数字预测模型训练实验，训练后的runner保存至runners字典中。

    # LSTM训练
lstm_runners = {}
lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    lstm_runners[length] = runner

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6

    运行结果：
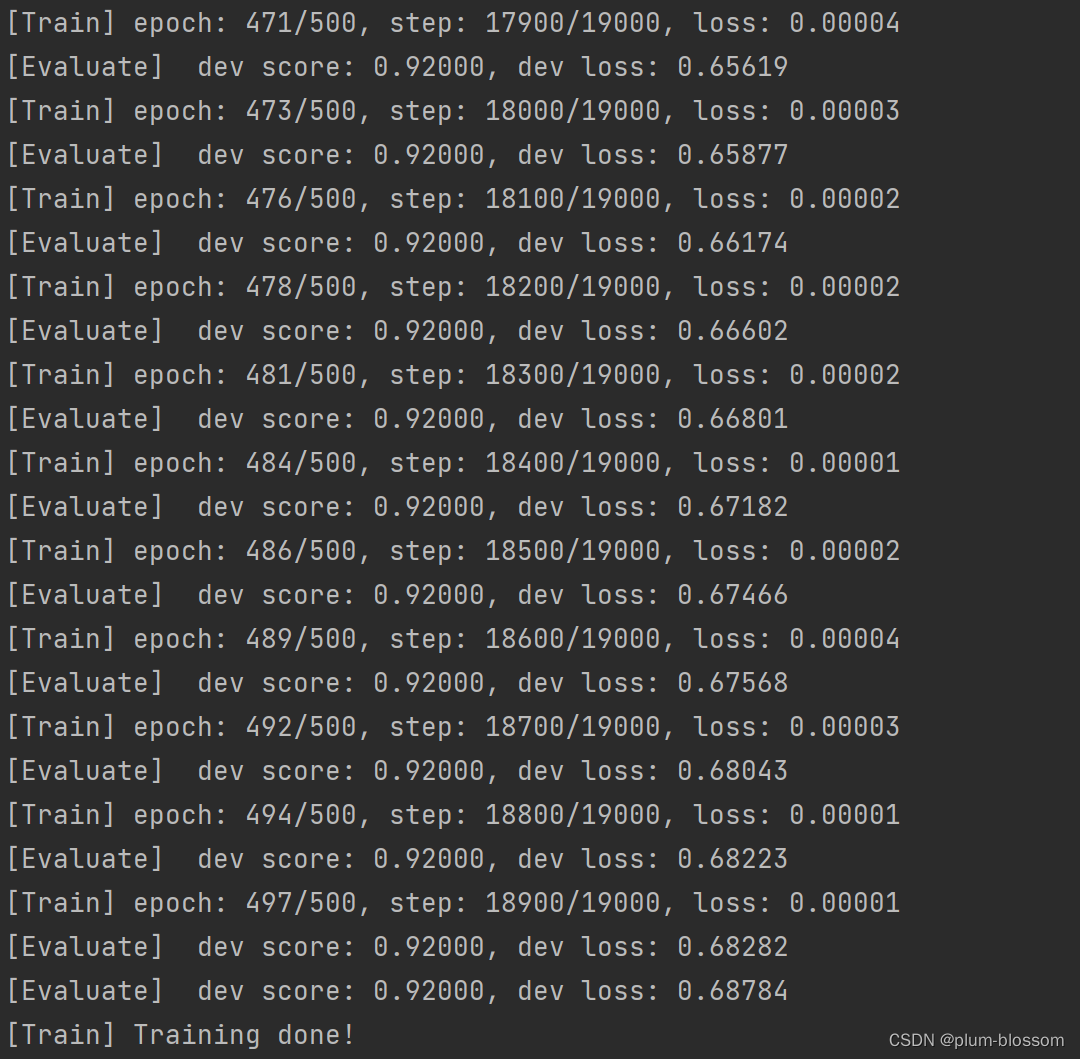
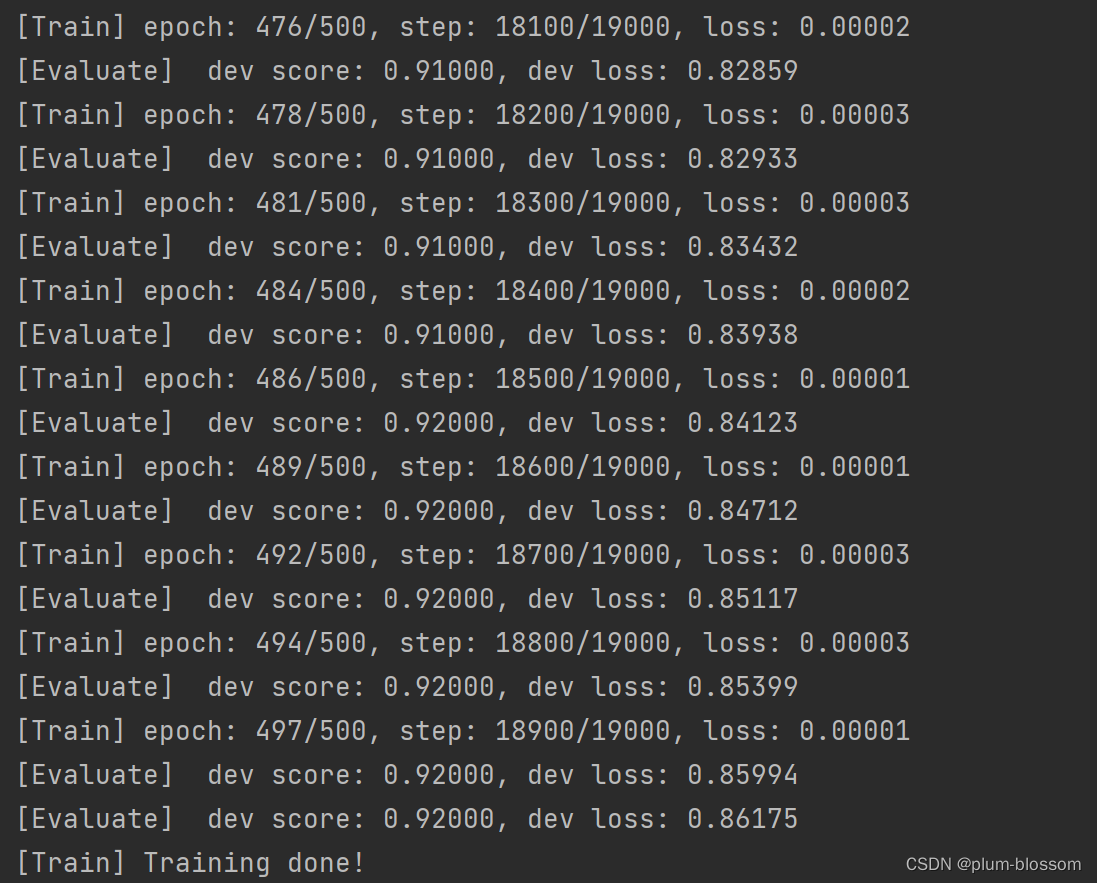
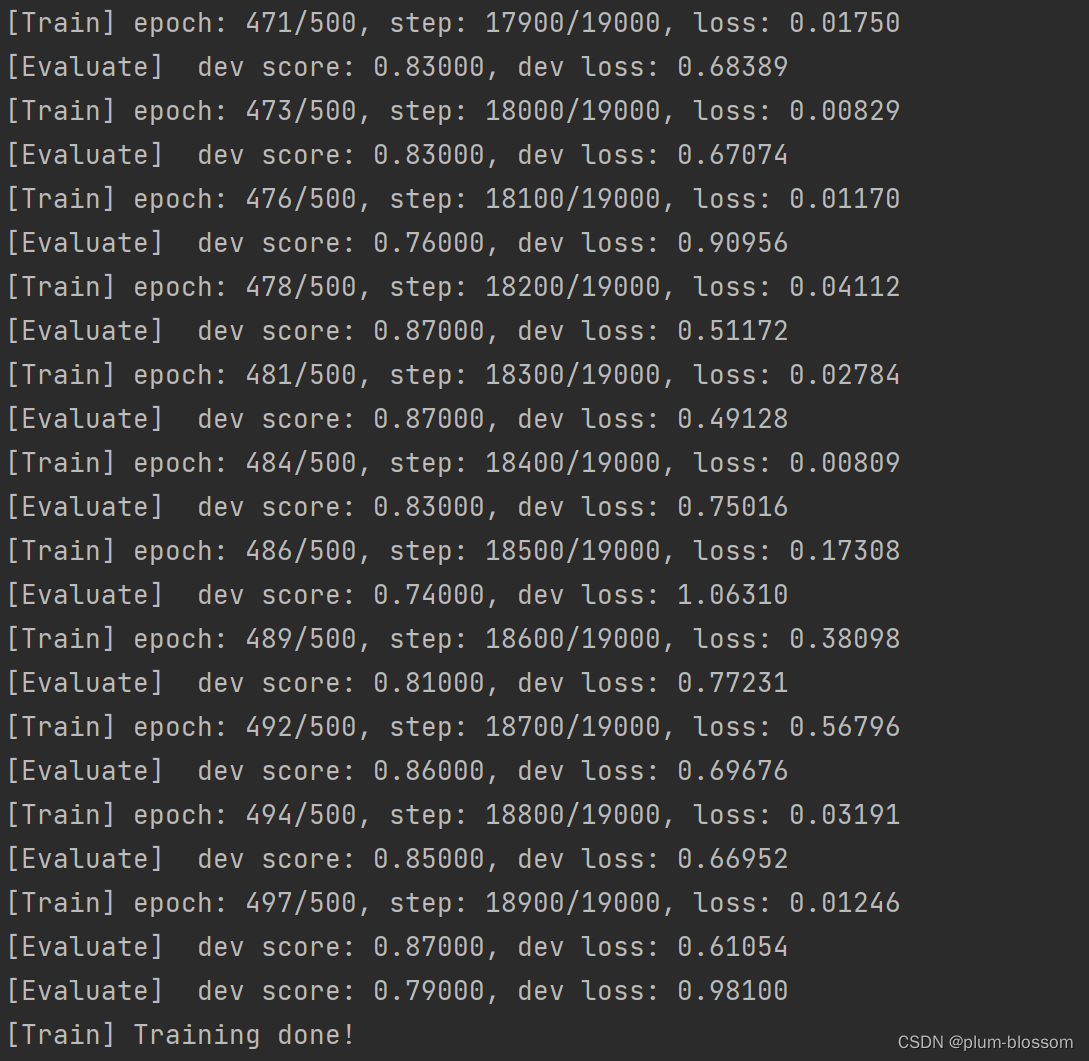
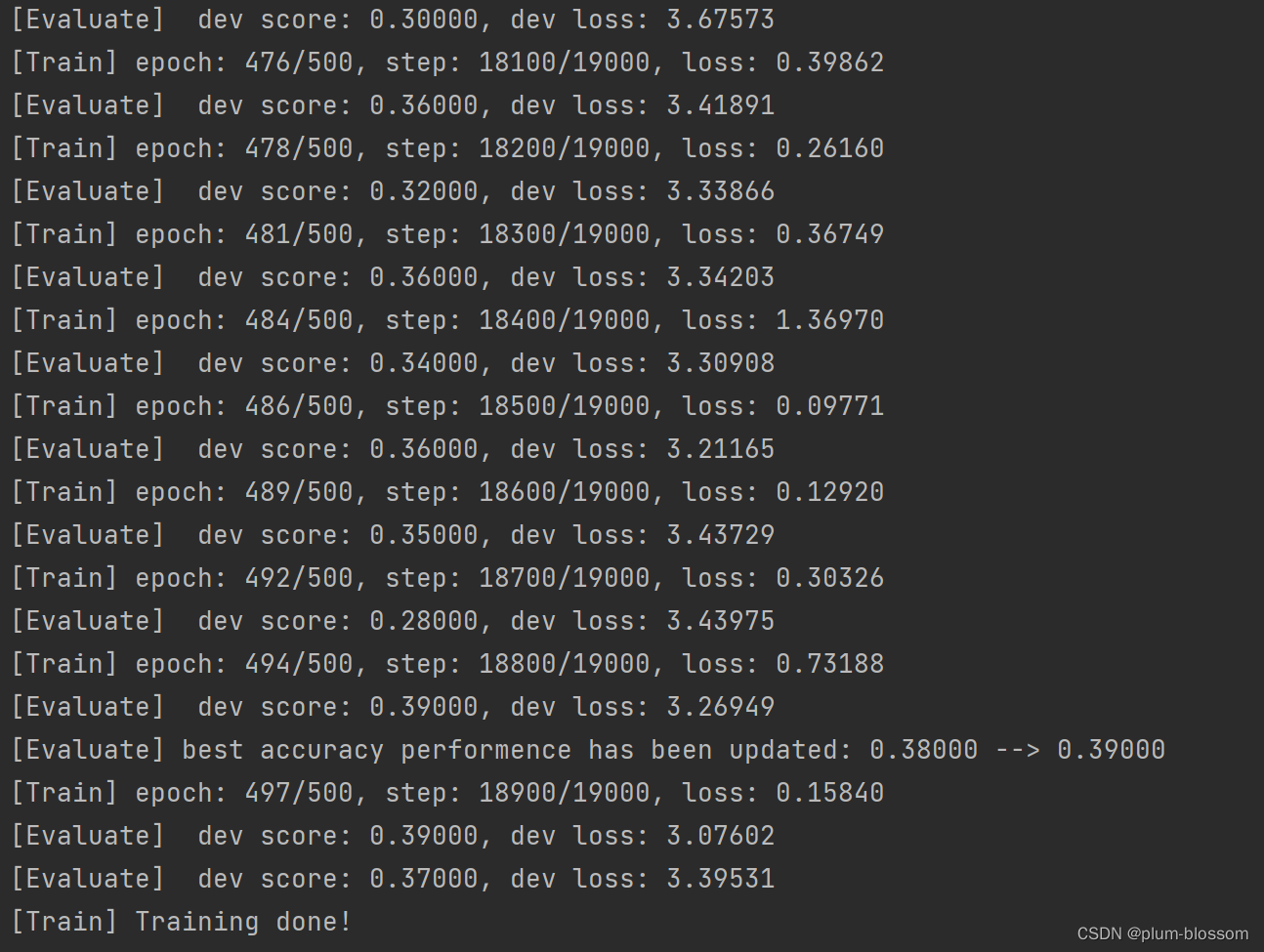
    在这里插入图片描述
    在这里插入图片描述

    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    6.3.2.3 损失曲线展示
    # # 画出训练过程中的损失图
for length in lengths:
    runner = lstm_runners[length]
    fig_name = f"D:/datasets/images/6.11_{length}.pdf"
    plot_training_loss(runner, fig_name, sample_step=100)

    • 1
    • 2
    • 3
    • 4
    • 5

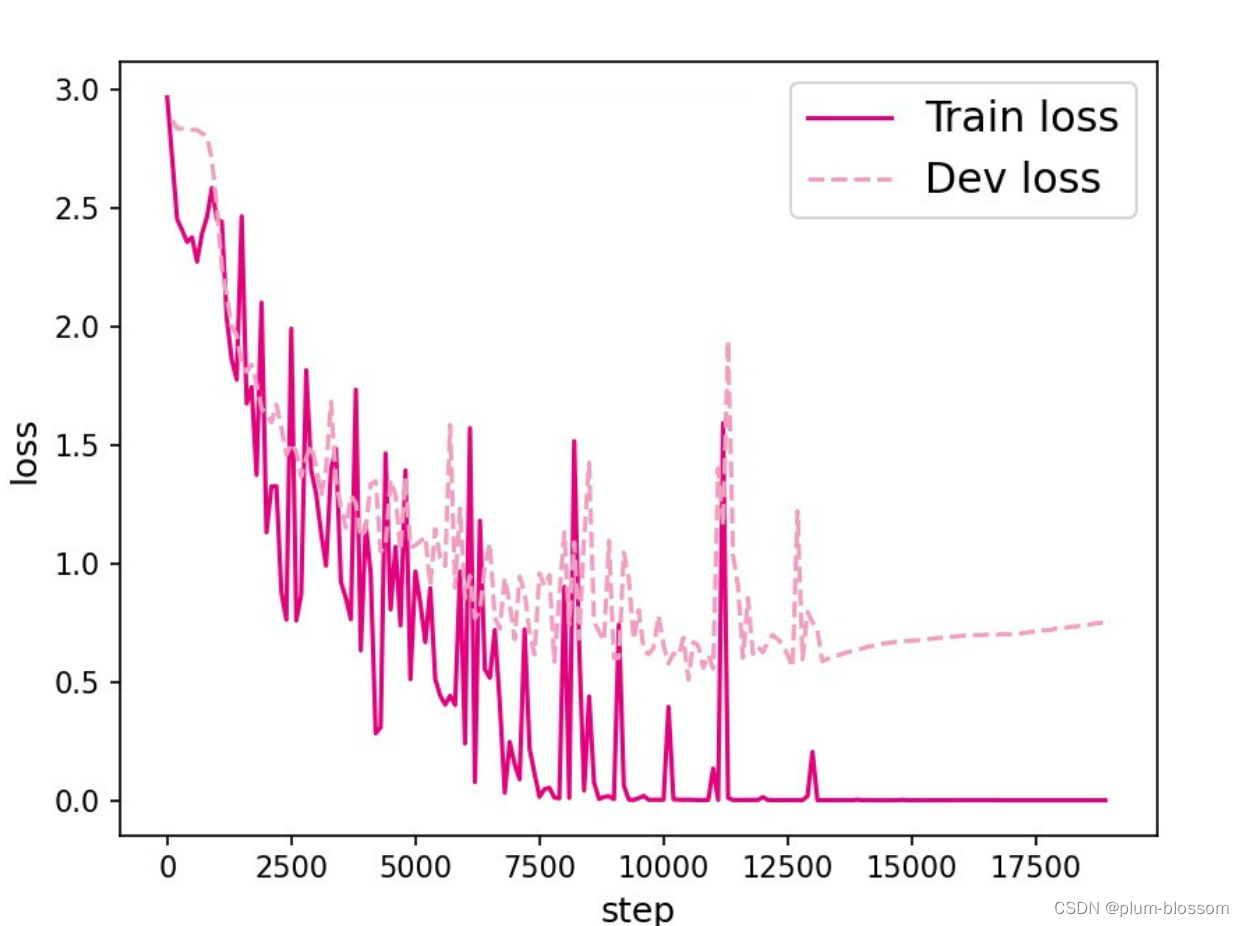
    L=10：
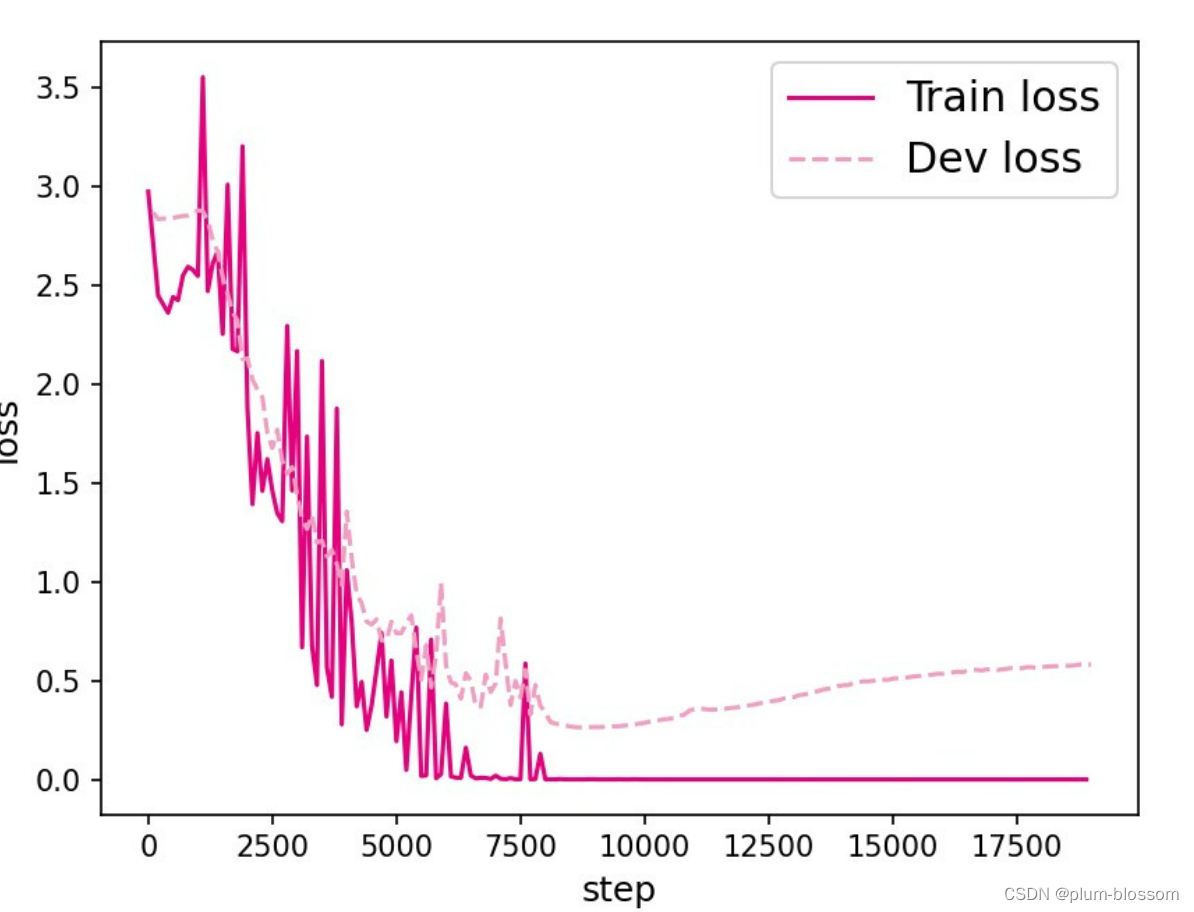
    在这里插入图片描述

    L=15：
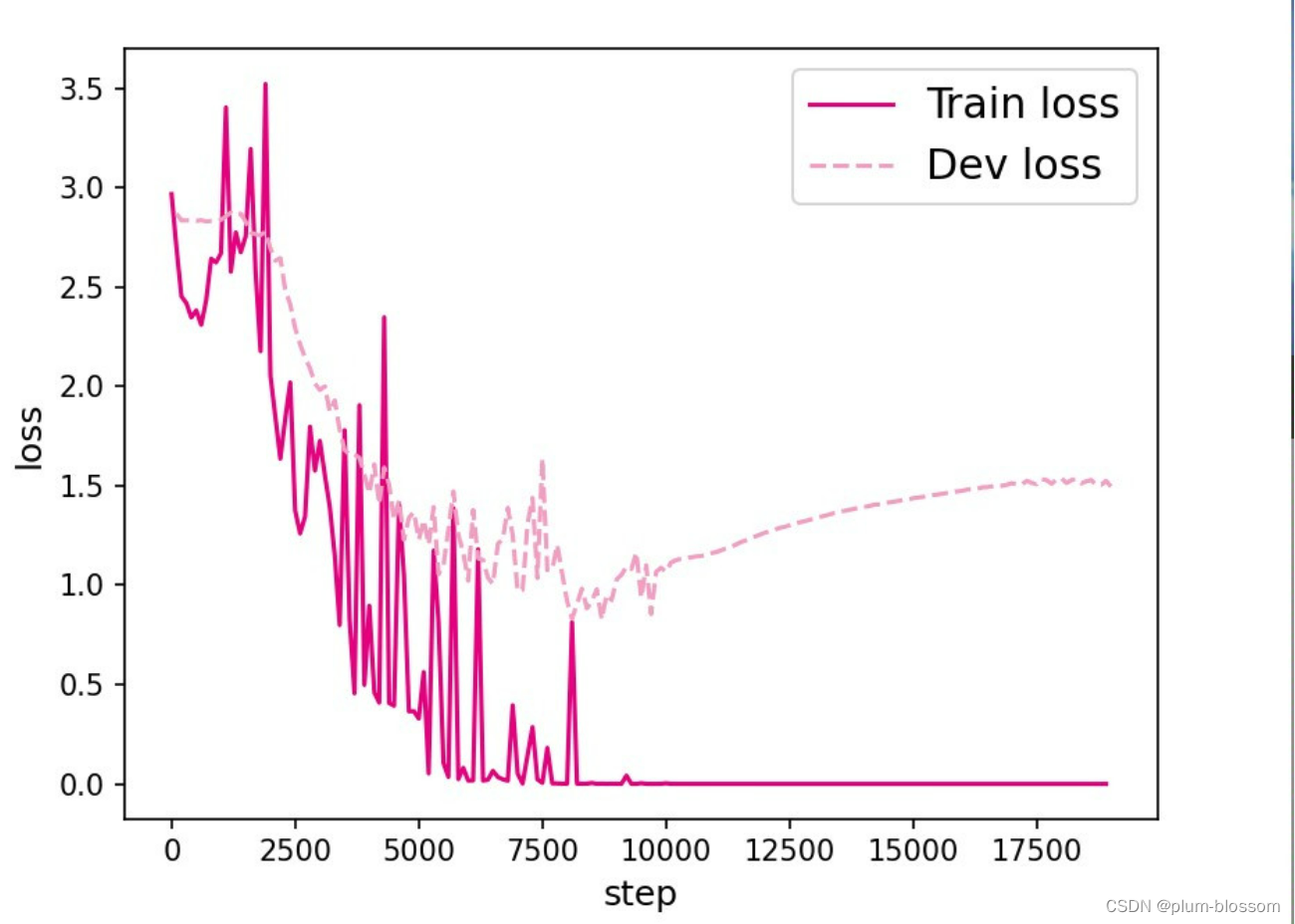
    在这里插入图片描述

    L=20：
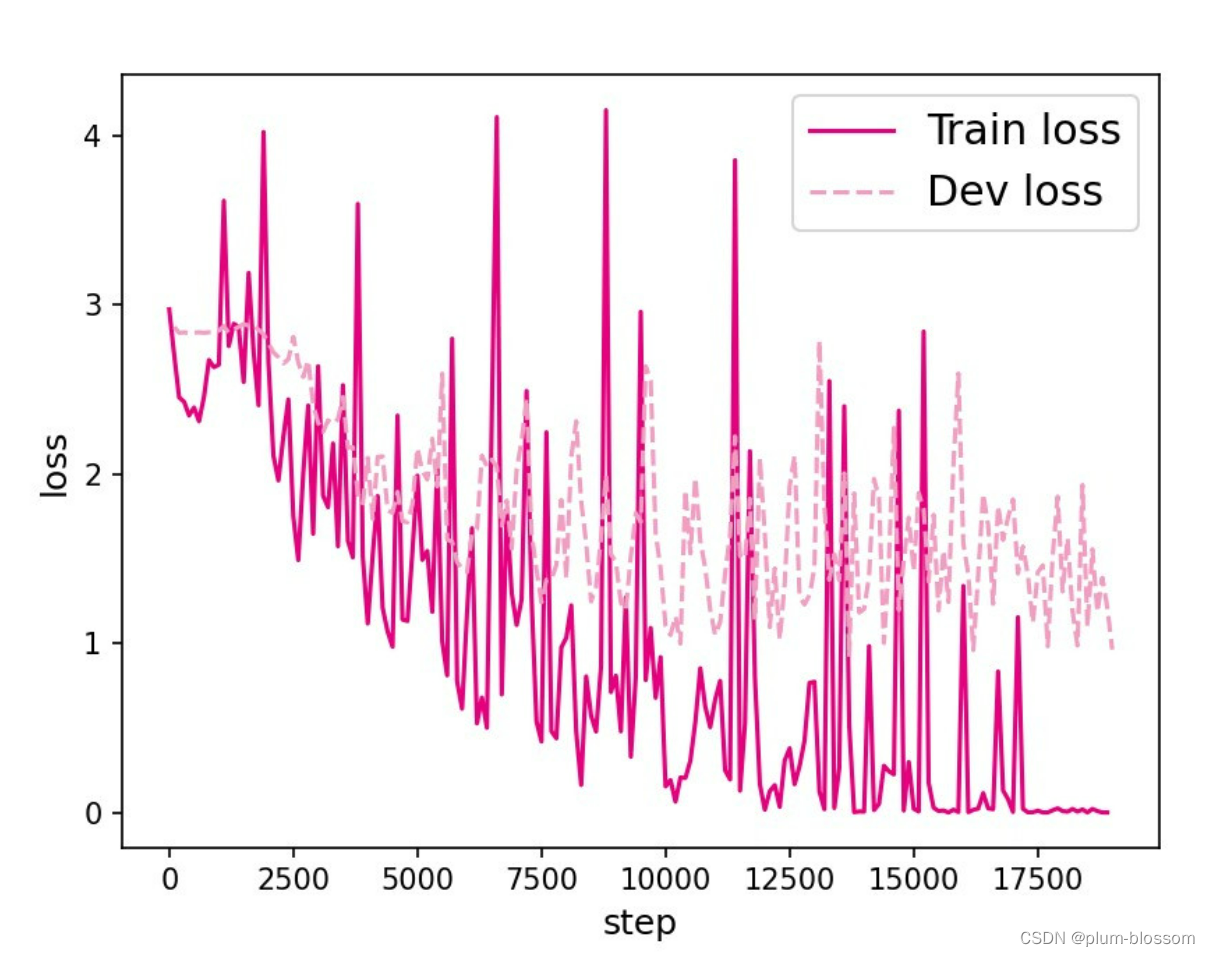
    在这里插入图片描述

    L=25：
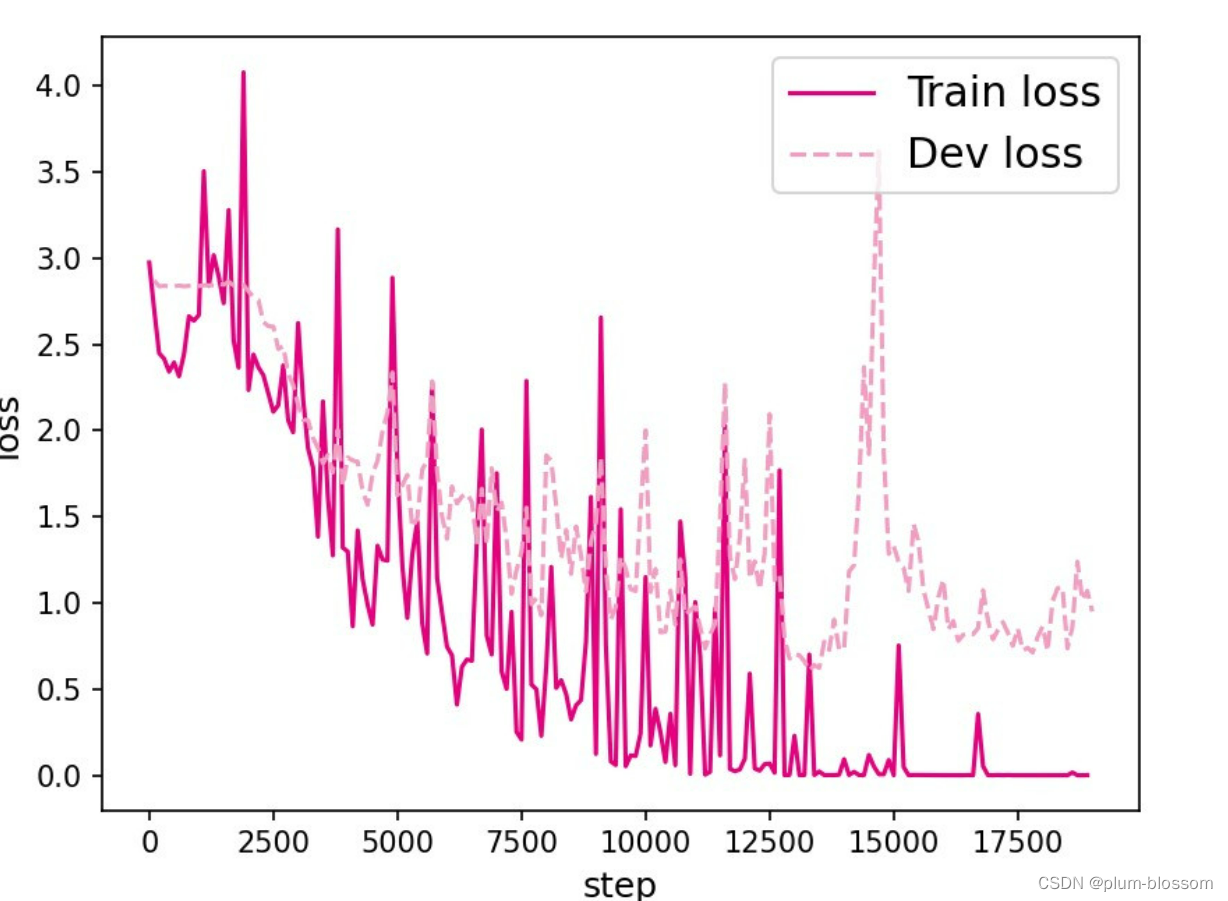
    在这里插入图片描述

    L=30：
    在这里插入图片描述

    L=35：
    在这里插入图片描述

    【思考题1】LSTM与SRN实验结果对比，谈谈看法。（选做）

    LSTM模型在不同长度数据集上进行训练后的损失变化，同SRN模型一样，随着序列长度的增加，训练集上的损失逐渐不稳定，验证集上的损失整体趋向于变大，这说明当序列长度增加时，保持长期依赖的能力同样在逐渐变弱。LSTM模型在序列长度增加时，收敛情况比SRN模型更好，确率也要优于SRN。

    6.3.3 模型评价

    6.3.3.1 在测试集上进行模型评价
    #lstm
lstm_dev_scores = []
lstm_test_scores = []
for length in lengths:
    print(f"Evaluate LSTM with data length {length}.")
    runner = lstm_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
    runner.load_model(model_path)

    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = DataLoader(test_set, batch_size=batch_size)

    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    lstm_test_scores.append(score)
    lstm_dev_scores.append(max(runner.dev_scores))

for length, dev_score, test_score in zip(lengths, lstm_dev_scores, lstm_test_scores):
    print(f"[LSTM] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")

#训练SRN模型
srn_runners = {}
lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    srn_runners[length] = runner
srn_dev_scores = []
srn_test_scores = []
for length in lengths:
    print(f"Evaluate SRN with data length {length}.")
    runner = srn_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_srn_model_{length}.pdparams")
    runner.load_model(model_path)

    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)

    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    srn_test_scores.append(score)
    srn_dev_scores.append(max(runner.dev_scores))

for length, dev_score, test_score in zip(lengths, srn_dev_scores, srn_test_scores):
    print(f"[SRN] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52

    运行结果：

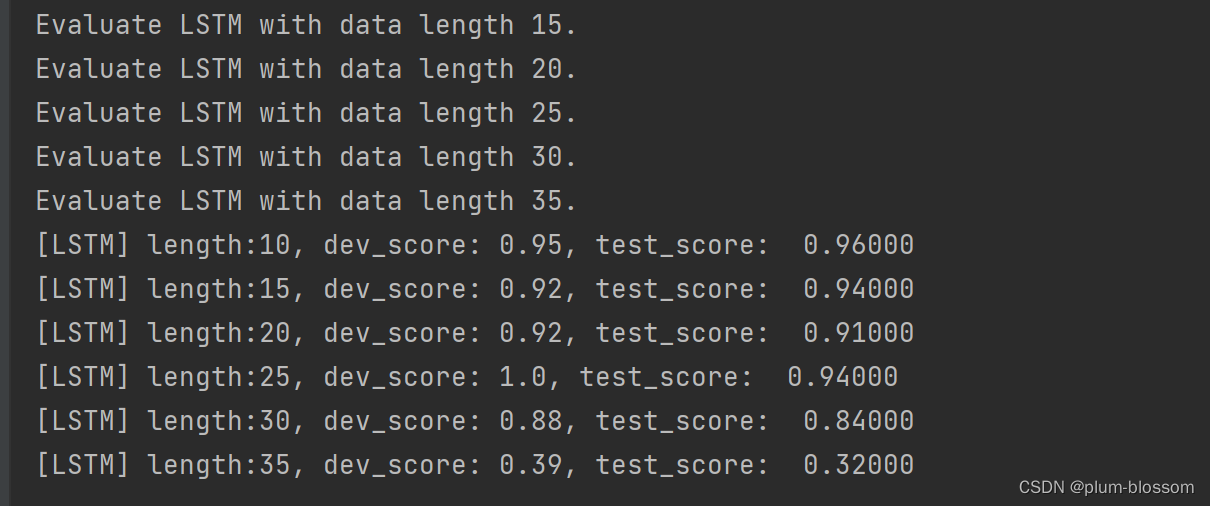
    在这里插入图片描述

    6.3.3.2 模型在不同长度的数据集上的准确率变化图
    #绘制全部图
import matplotlib.pyplot as plt

plt.plot(lengths, lstm_dev_scores, '-o', color='#e8609b',  label="LSTM Dev Accuracy")
plt.plot(lengths, lstm_test_scores,'-o', color='#000000', label="LSTM Test Accuracy")

#绘制坐标轴和图例
plt.ylabel("accuracy", fontsize='large')
plt.xlabel("sequence length", fontsize='large')
plt.legend(loc='lower left', fontsize='x-large')

fig_name = "D:/datasets/images/6.12.pdf"
plt.savefig(fig_name)
plt.show()

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14

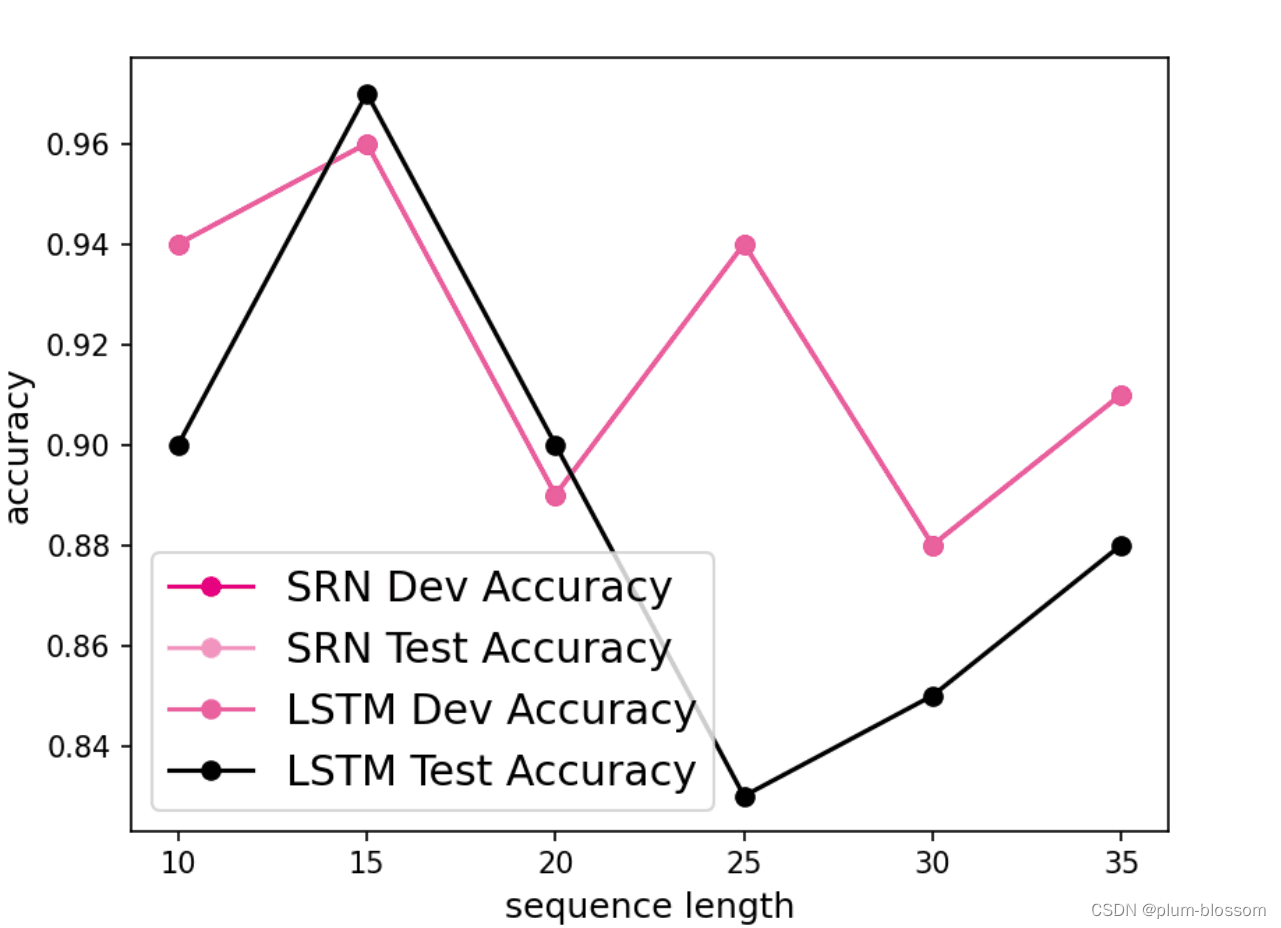
    在这里插入图片描述

    【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。（选做）

    随着数据集长度的增加，LSTM模型和SRN模型的准确率降低，但是LSTM模型的准确率显著高于SRN模型，说明LSTM模型保持长期依赖的能力要优于SRN模型。

    6.3.3.3 LSTM模型门状态和单元状态的变化
    import torch.nn.functional as F

# 实例化模型
model = LSTM(input_size, hidden_size)
model = Model_RNN4SeqClass(model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
lr = 0.001
optimizer = torch.optim.Adam(model.parameters(),lr)
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = torch.nn.CrossEntropyLoss()
# 基于以上组件，重新实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)

length = 10
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
runner.load_model(model_path)

import seaborn as sns

def plot_tensor(inputs, tensor,  save_path, vmin=0, vmax=1):
    import matplotlib.pyplot as plt
    tensor = np.stack(tensor, axis=0)
    tensor = np.squeeze(tensor, 1).T

    plt.figure(figsize=(16,6))
    # vmin, vmax定义了色彩图的上下界
    ax = sns.heatmap(tensor, vmin=vmin, vmax=vmax)
    ax.set_xticklabels(inputs)
    ax.figure.savefig(save_path)


# 定义模型输入
inputs = [6, 7, 0, 0, 1, 0, 0, 0, 0, 0]
X = torch.tensor(inputs.copy())
X = X.unsqueeze(0)
# 进行模型预测，并获取相应的预测结果
logits = runner.predict(X)
predict_label = torch.argmax(logits, dim=-1)
print(f"predict result: {predict_label.numpy()[0]}")
# 输入门
Is= runner.model.rnn_model.Is
plot_tensor(inputs, Is, save_path="D:/datasets/images/6.13_I.pdf")
# 遗忘门
Fs = runner.model.rnn_model.Fs
plot_tensor(inputs, Fs, save_path="D:/datasets/images/6.13_F.pdf")
# 输出门
Os = runner.model.rnn_model.Os
plot_tensor(inputs, Os, save_path="D:/datasets/images/6.13_O.pdf")
# 单元状态
Cs = runner.model.rnn_model.Cs
plot_tensor(inputs, Cs, save_path="D:/datasets/images/6.13_C.pdf", vmin=-5, vmax=5)


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55

    输出门：
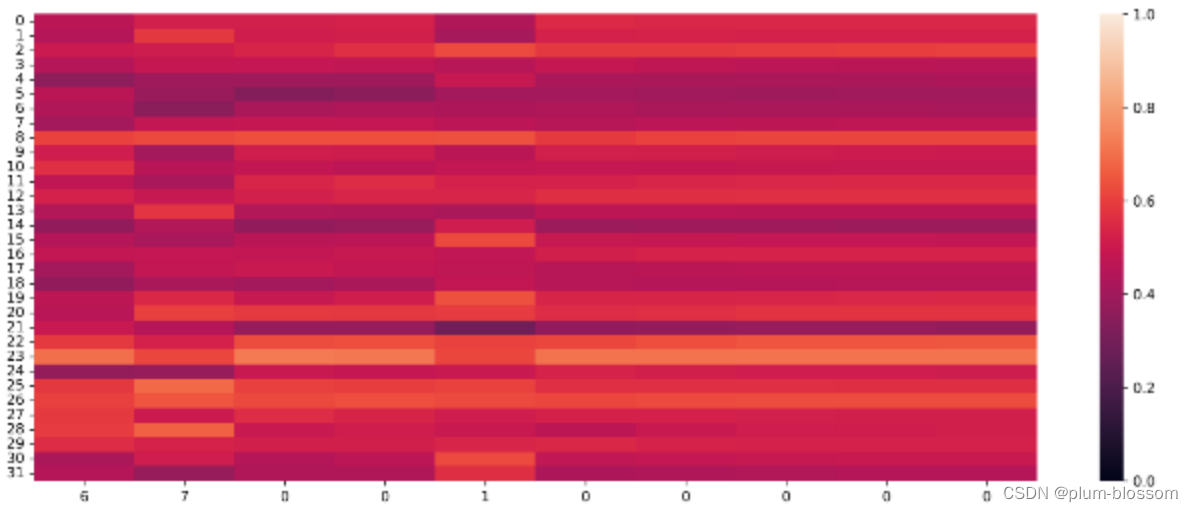
    在这里插入图片描述

    遗忘门：
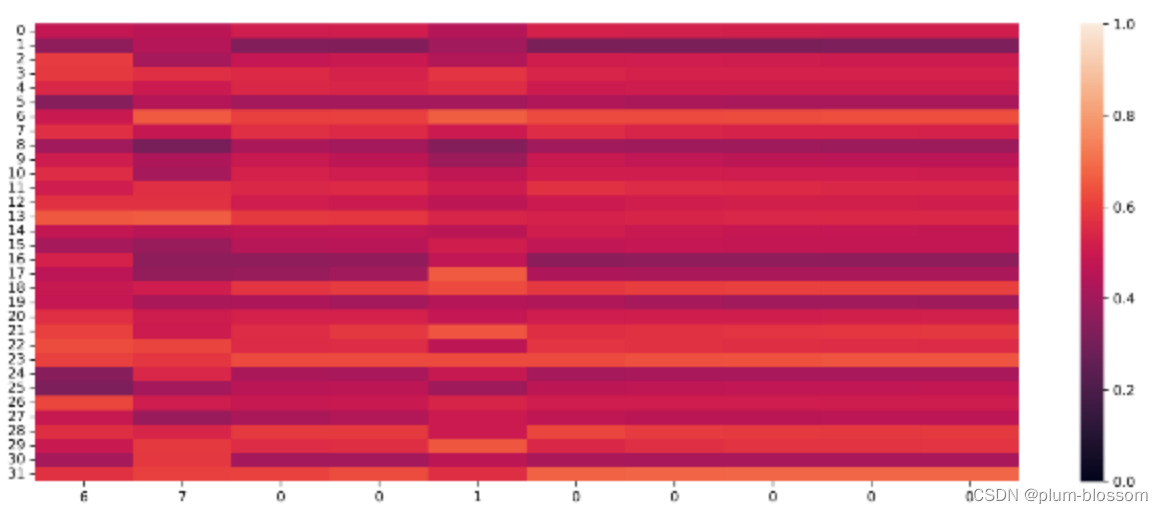
    在这里插入图片描述

    输入门：
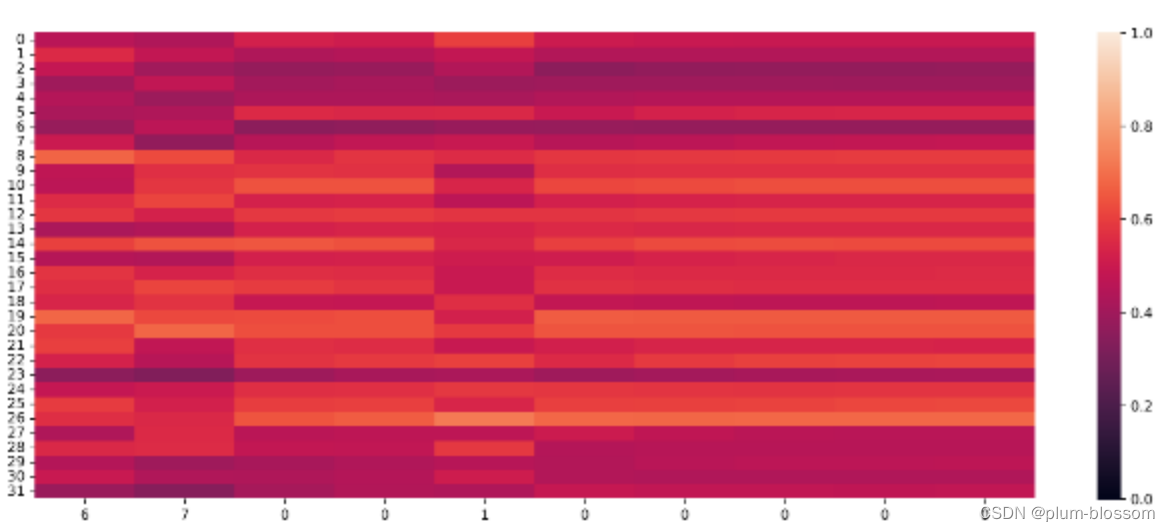
    在这里插入图片描述

    单元状态：
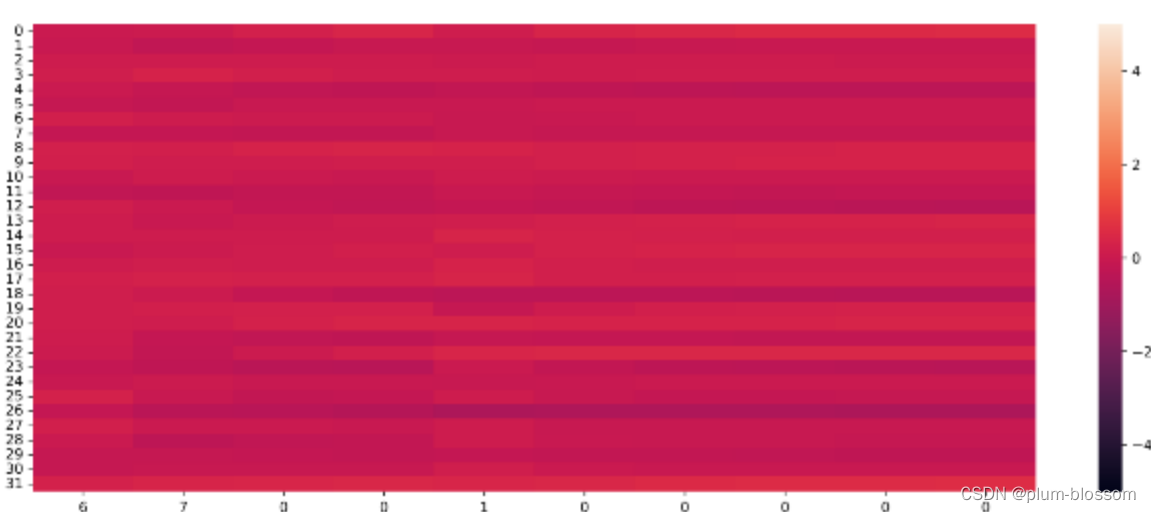
    在这里插入图片描述

    【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。

    横坐标为输入数字，纵坐标为相应门或单元状态向量的维度，颜色的深浅代表数值的大小。
    当输入门遇到不同位置的数字0时，保持了相对一致的数值大小，表明对于0元素保持相同的门控过滤机制，避免输入信息的变化给当前模型带来困扰；
    遗忘门数值在一些维度上变小，表明对某些信息进行了遗忘；
    输出门和单元状态在某些维度上数值变小，在某些维度上数值变大，表明输出门在根据信息的重要性选择信息进行输出，同时单元状态也在保持着对文本预测重要的一些信息.

    全面总结RNN（必做）

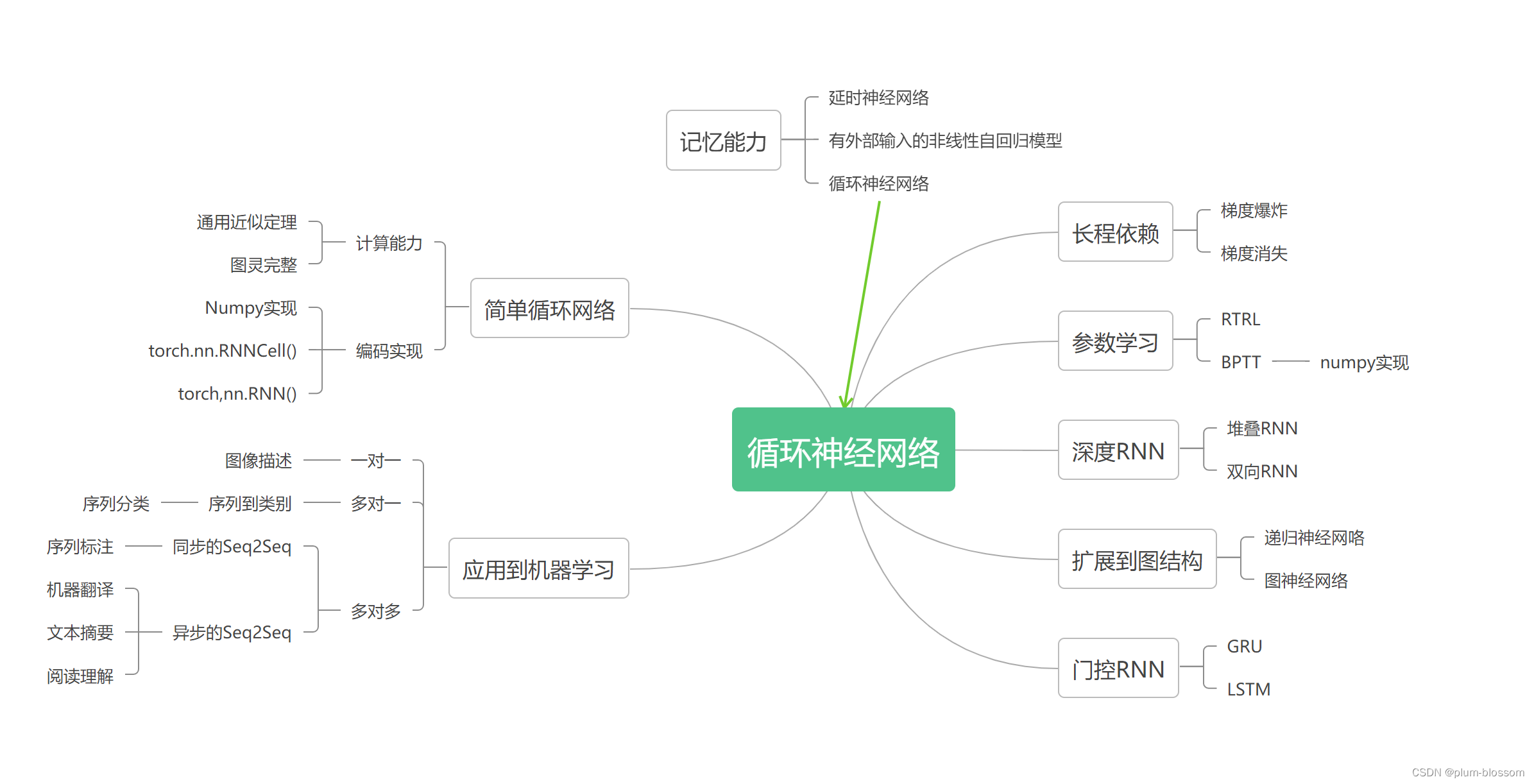
    在这里插入图片描述

    ref：

    NNDL 实验6（上） - HBU_DAVID - 博客园 (cnblogs.com)

    NNDL 实验6（下） - HBU_DAVID - 博客园
    (cnblogs.com)

  • 相关阅读:
    给某个伙伴展示一次渗透提权
    JPA在不写sql的情况下实现模糊查询
    php-fpm未授权访问漏洞
    unity 使用声网（Agora）实现语音通话
    ++ Reference: Standard C++ Library reference: C Library: cmath: lround
    实践 缓存
    GIS数据漫谈（六）— 投影坐标系统
    Windows 10 + Jenkins 2.4 安装插件时https 的证书问题及解决
    超级浏览器对跨境亚马逊防关联有用吗？
    Python 教程之控制流（7）Python中的链接比较运算符
  • 原文地址：https://blog.csdn.net/qq_51713698/article/details/128074787