关于如何找环形链表的入环点

一、判断一个链表是否有环

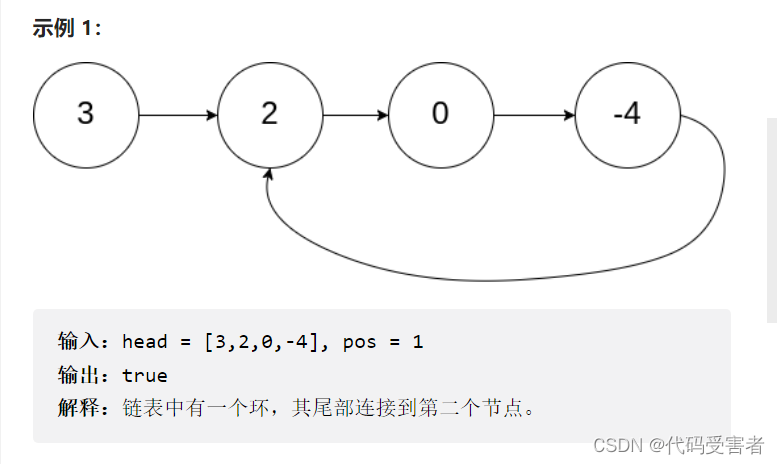
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
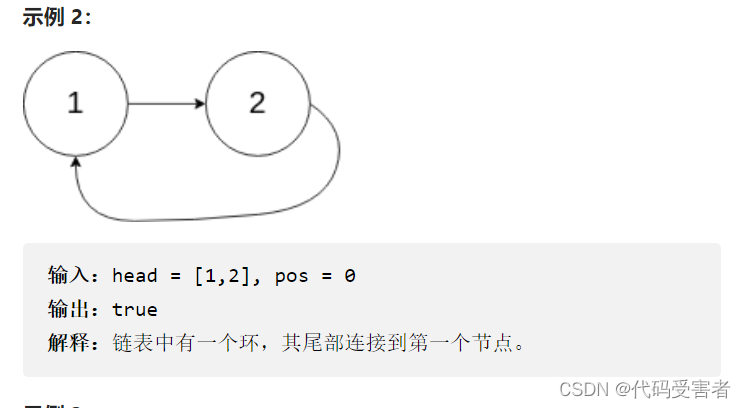
如果链表中存在环 ，则返回 true 。 否则，返回 false 。



解题思路:

用快慢指针，慢指针一次往后走一步，快指针一次往后走两步。这样快指针会比慢指针先入环，当慢指针入环被快指针追上时，说明这是一个环形链表，当快指针为空或者指向空时，说明这不是环形链表，返回NULL。

为什么肯定slow 和 fast一定会相遇呢？我们假设当slow入环时，fast到slow的距离为N。

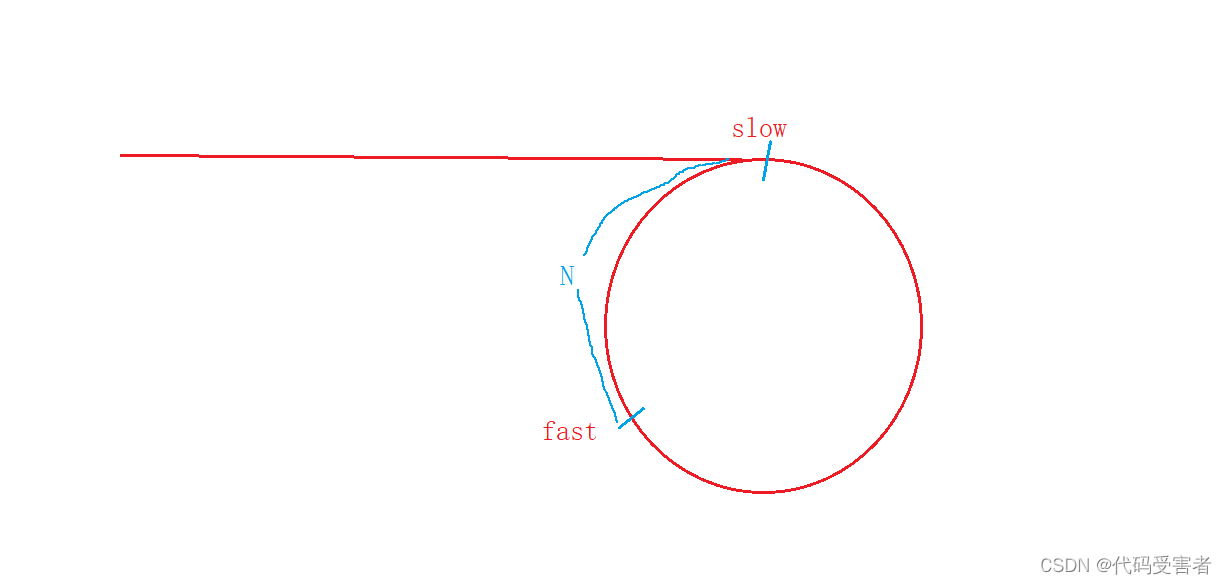
而slow 每次往前走一步，fast 每次往前走两步，那么它们的距离是逐渐递减的。

最后它们之间的距离为 0 时，它们就相遇了。

那问题来了，如果fast 一次走三步，四步，五步，它能不能在环中与slow相遇呢？ 我们假设fast一次走三步。
fast到slow的距离继续为N

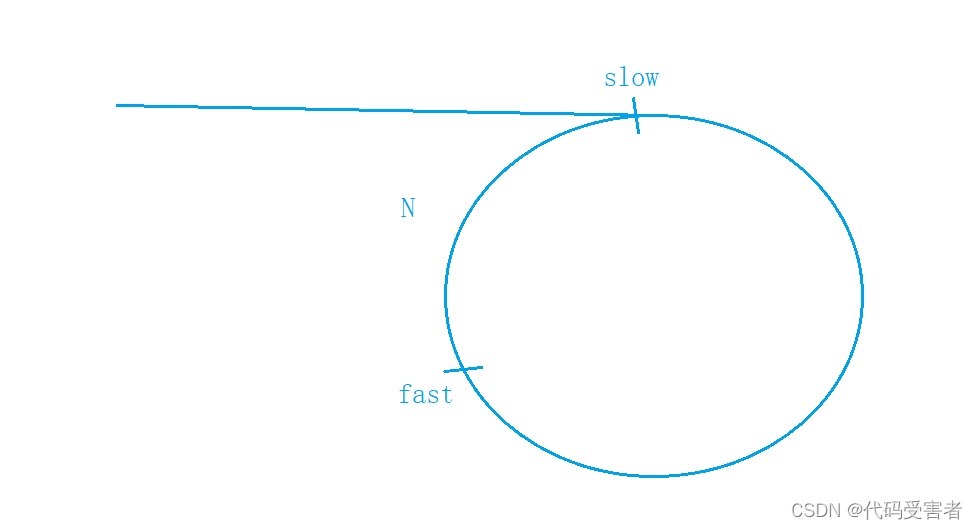
slow 一次走一步， fast一次走三步 ， 那么N是每次少2

此时会出现两者情况，一种情况是相遇了，还有一种情况是没相遇。
当没相遇的时候，fast已经跑到了 slow的前面，也就是它们此时的距离是-1。

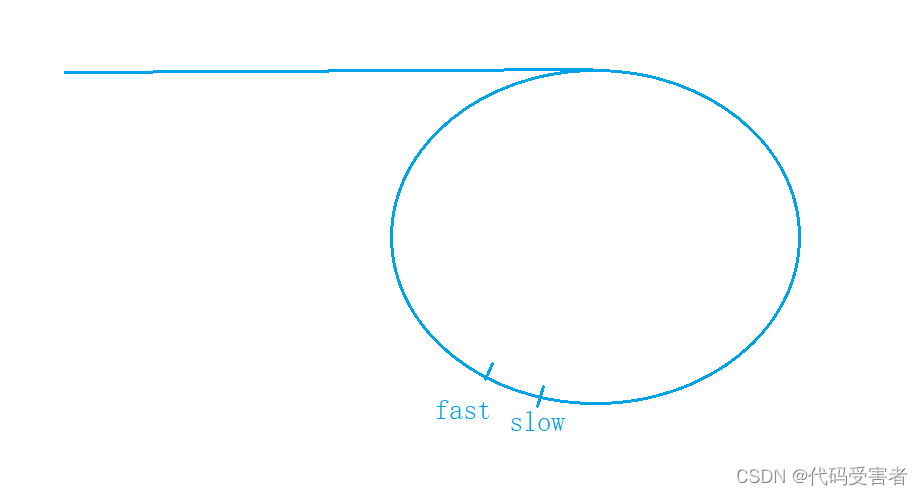
设这个环的长度为C，所以它们的距离 N 此时是等于 C-1的。而因为fast一次是走三步的，所以N每次会-2。 当N等于0时它们才会相遇，这也就意味，C-1 如果是偶数，那么它们才会相遇，如果C-1 是奇数，那它们永远不会相遇。所以，fast 一次走两步，它一定会和slow在环里面相遇，slow不用走完一圈。如果fast一次走3，4，5…n步，那么是有可能永远不会与slow相遇的。

代码如下:

bool hasCycle(struct ListNode *head) {
   
    struct ListNode* slow = head;
    struct ListNode* fast = head;

    //如果fast为空或者指向空，说明不是环形链表
    while(fast 
1
2
3
4
5
6