搜索技术——遗传算法

如果有兴趣了解更多相关内容，欢迎来我的个人网站看看：瞳孔空间

一：进化与遗传的概念

拉马克(Lamarck)进化论：

• 一切物种都是其他物种演变和进化而来的，而生物的演变和进化是一个缓慢和连续的过程
• 环境的变化能够引起生物的变异，环境的变化迫使生物发生适应性的进化
• 有神经系统的动物发生变异的原因，除了环境变化和杂交外，更重要是通过用进废退和获得性状遗传
• 生物进化的方向从简单到复杂，从低到高
• 最原始的生物起源于自然发生。生物并不起源于共同祖先
• 拉马克曾以长颈鹿的进化为例，说明他的“用进废退”观点。长颈鹿的祖先颈部并不长，由于干旱等原因。在低处已找不到食物，迫使它伸长脖颈去吃高处的树叶，久而久之，它的颈部就变长了。一代又一代，遗传下去，它的脖子越来越长，终于进化为现在我们所见的长颈鹿

达尔文(Darwin)进化论：

• 包括两部分：遗传(基因)变异；自然选择
• 生物不是静止的，而是进化的。物种不断变异，旧物种消灭，新物种产生
• 生物的进化是连续和逐渐，不会发生突变
• 生物之间存在一定的亲缘关系，他们具有共同的祖先
• 自然选择。生物过渡繁殖，但是它们的生存空间和食物有限，从而面临生存斗争，包括：种内、种间以及生物与环境的斗争。自然选择是达尔文进化论的核心
• 达尔文摒弃了Lamarck获得性遗传法则
• 胚胎学家Weismann用如下实验：22代连续切割小鼠尾巴而第23代小鼠尾巴仍然不变短，明确否定了获得性遗传的观点

孟德尔学说：1857年，身为神父的孟德尔通过对植物进行一系列仔细的实验，发现植物的父母单独地把自身的特征传递给下一代。至关重要的是，他还发现特征不是单纯地混合在一起，而是保持着独立性：一株高的植物和一株矮的植物繁殖出来的后代要么是高的，要么是矮的，而不是介于两者之间。表明特征是分开独立地遗传给下一代，后来这被称为遗传基因。让人惊奇的是，孟德尔的重要发现被人们忽略了数十年，直到20世纪初才被人们认可。

新达尔文主义：

• 将达尔文进化论和孟德尔-摩根基因相结合，成为现被广泛接受的新达尔文主义
• 新达尔文注意认为，只用种群上和物种内的少量统计过程就可以充分地解释大多数生命历史，这些过程就是繁殖、变异、竞争、选择。繁殖是所有生命的共同特性；变异保证了任何生命系统能在正熵世界中连续繁殖自己；对于限制在有限区域中的不断膨胀的种群来说，竞争和选择是不可避免的结论

生物中的遗传概念：

• 在生物细胞中，控制并决定生物遗传特性的物质是脱氧核糖核酸，简称DNA。染色体是其载体
• DNA是由四种碱基按一定规则排列组成的长链。四种碱基不同的排列决定了生物不同的表现性状。例如，改变DNA长链中的特定一段（称为基因），即可改变人体的身高
• 细胞在分裂时，DNA通过复制而转移到新产生的细胞中，新的细胞就继承了上一代细胞的基因
• 在繁殖下一代时，两个同源染色体之间通过交叉而重组，亦即在两个染色体的某一相同位置处DNA被切断，其前后两串分别交叉形成两个新的染色体
• 在细胞进行复制时可能以很小的概率产生某些复制差错，从而使DNA发生某种变异，产生新的染色体
• 这些新的染色体将决定新的个体（后代）的新的性状
• 在一个群体中，并不是所有的个体都能得到相同的繁殖机会，对生存环境适应度高的个体将获得更多的繁殖机会；对生存环境适应度较低的个体，其繁殖机会相对较少，即所谓自然选择。而生存下来的个体组成的群体，其品质不断得以改良，称为进化。
• 生物的进化是经过无数次有利的进化积累而成的，不同的环境保留了不同的变异后代

二：遗传算法

2.1：基本介绍

遗传算法(Genetic Algorithm，GA)最早是由美国的John holland于20世纪70年代提出，该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

遗传算法通过数学的方式，利用计算机仿真运算，将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时，相对一些常规的优化算法，通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

遗传算法的发展：

• 1967年，美国密歇根大学约翰·霍兰德(John Holland)教授的学生Bagley在他的博士论文中首次提出了遗传算法这一术语，此后，Holland指导学生完成了多篇有关遗传算法研究的论文。1971年，Hollstien在他的博士论文中首次把遗传算法用于函数优化
• 1975年是遗传算法研究历史上十分重要的一年。这一年约翰·霍兰德(John Holland)出版了他的著名专著《自然系统和人工系统的适应性》，该书系统地阐述了遗传算法的基本理论和方法，并提出了对遗传算法极为重要的模式理论，该理论首次确认了结构重组遗传操作对于获得隐并行性的重要性
• 同年，迪乔恩(K.A.De Jong)完成了他的重要论文《遗传自适应系统的行为分析》。他在该论文中所做的研究工作可看作是遗传算法发展过程中的一个里程碑。他把Holland的模式理论与他的计算实验结合起来。尽管迪乔恩主要侧重于函数优化的应用研究，但他将选择、交叉和变异操作进一步完善和系统化，同时又提出了诸如代沟(generation gap)等新的遗传操作技术。他的研究工作为遗传算法及其应用打下了坚实的基础，他所得出的许多结论，迄今仍具有普遍的指导意义
• 20世纪80年代后，遗传算法进入兴盛发展时期，被广泛应用于自动控制、生产计划、图像处理、机器人等研究领域

遗传算法的基本思想：

• 首先实现从问题到基因映射，即编码(问题表示)工作，然后从代表问题可能潜在解集得一个种群开始进行进化求解
• 初代种群(编码集合)产生后，按照优胜劣汰的原则，根据个体适应度大小挑选(选择)个体，进行复制、交叉、变异，产生出代表新的解集的群体，再对其进行挑选以及一系列遗传操作，如此往复，逐代演化产生出越来越好的近似解

概念说明：

• 选择：通过适应度的计算，淘汰不合理的个体。类似于自然界的物竞天择
• 复制：编码的拷贝，类似于细胞分裂中染色体的复制
• 交叉：编码的交叉重组，类似于染色体的交叉重组
• 变异：编码按小概率扰动产生的变化，类似于基因的突变

这个过程将导致种群像自然进化一样，后代种群比前代更加适应环境，末代种群中得最优个体经过解码（从基因到问题的映射），可以作为问题近似最优解。

遗传算法：

• 遗传算法直接以目标函数值作为搜索信息
• 传统的优化算法往往不只需要目标函数值，还需要目标函数的导数等其它信息。这样对许多目标函数无法求导或很难求导的函数，遗传算法就比较方便
• 遗传算法同时进行解空间的多点搜索
• 传统的优化算法往往从解空间的一个初始点开始搜索，这样容易陷入局部极值点
• 遗传算法进行群体搜索，而且在搜索的过程中引入遗传运算，使群体又可以不断进化。这些是遗传算法所特有的一种隐含并行性

随机搜索 + 定向搜索：

• 遗传算法使用概率搜索技术。遗传算法属于一种自适应概率搜索技术，其选择、交叉、变异等运算都是以一种概率的方式来进行的，从而增加了其搜索过程的灵活性
• 实践和理论都已证明了在一定条件下遗传算法总是以概率1收敛于问题的最优解

用遗传算法求解问题需要解决以下六个问题：

• 编码：GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的不同组合便构成了不同的点
• 初始群体的生成：随机产生N个初始串结构数据，每个串结构数据称为一个个体，N个个体构成了一个群体。GA以这N个串结构数据作为初始点开始进化
• 适应度评估：适应度表明个体或解的优劣性。不同的问题，适应性函数的定义方式也不同
• 选择：选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。遗传算法通过选择过程体现这一思想，进行选择的原则是适应性强的个体为下一代贡献一个或多个后代的概率大。选择体现了达尔文的适者生存原则
• 交叉：交叉操作是遗传算法中最主要的遗传操作。通过交叉操作可以得到新一代个体，新个体组合了其父辈个体的特性。交叉体现了信息交换的思想
• 变异：变异首先在群体中随机选择一个个体，对于选中的个体以一定的概率随机地改变串结构数据中某个串的值。同生物界一样，GA中变异发生的概率很低，通常取值很小

2.2：概念说明

编码问题：把解决的问题映射成一个数学问题，也就是所谓的“数学建模”或问题表示，那么这个问题的一个可行解即被称为一条“染色体”。编码的方法直接影响到了遗传算法的交叉算子、变异算子等遗传算子的运算，因此很大程度上决定了遗传进化的效率。

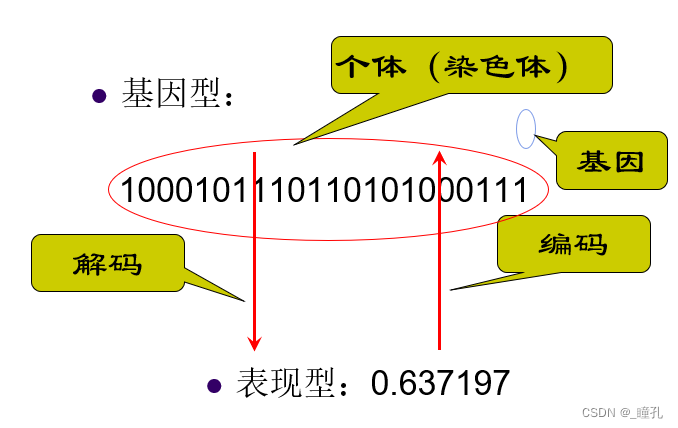
基因型（Genotype）：在自然界中，通过基因型表征繁殖，繁殖和突变，基因型是组成染色体的一组基因的集合。在遗传算法中，每个个体都由代表基因集合的染色体构成。例如，一条染色体可以表示为二进制串，其中每个位代表一个基因。

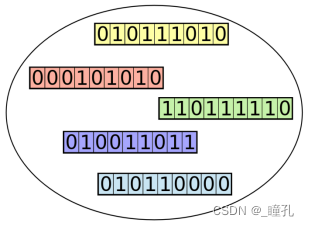
种群（Population）：遗传算法保持大量的个体（individuals）——针对当前问题的候选解集合。由于每个个体都由染色体表示，因此这些种族的个体（individuals）可以看作是染色体集合：

适应度函数（Fitness function）：在算法的每次迭代中，使用适应度函数（也称为目标函数）对个体进行评估。目标函数是用于优化的函数或试图解决的问题。适应度得分更高的个体代表了更好的解，其更有可能被选择繁殖并且其性状会在下一代中得到表现。随着遗传算法的进行，解的质量会提高，适应度会增加，一旦找到具有令人满意的适应度值的解，终止遗传算法。

选择（Selection）：在计算出种群中每个个体的适应度后，使用选择过程来确定种群中的哪个个体将用于繁殖并产生下一代，具有较高值的个体更有可能被选中，并将其遗传物质传递给下一代。也有机会选择低适应度值的个体，但概率较低。这样，就不会完全摒弃其遗传物质。

交叉（Crossover）：为了创建一对新个体，通常将从当前代中选择的双亲样本的部分染色体互换（交叉），以创建代表后代的两个新染色体。此操作称为交叉或重组：

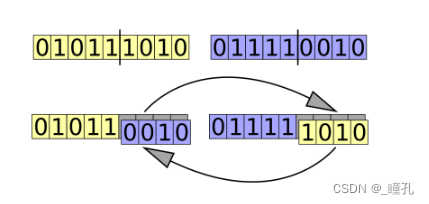
交叉策略分为单点交叉运算与两点交叉运算

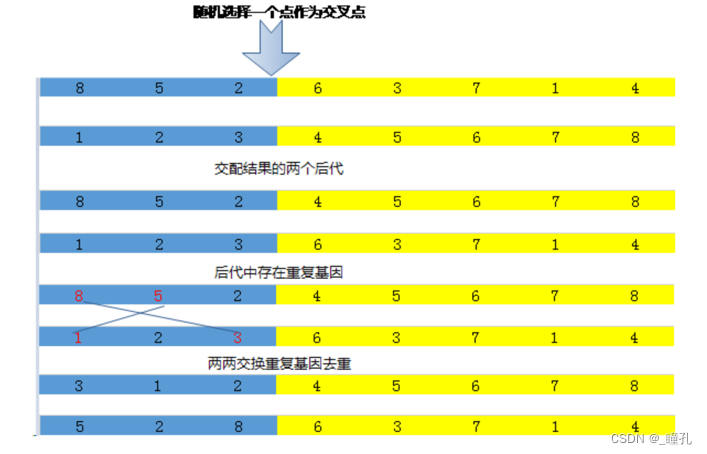
单点交叉运算：

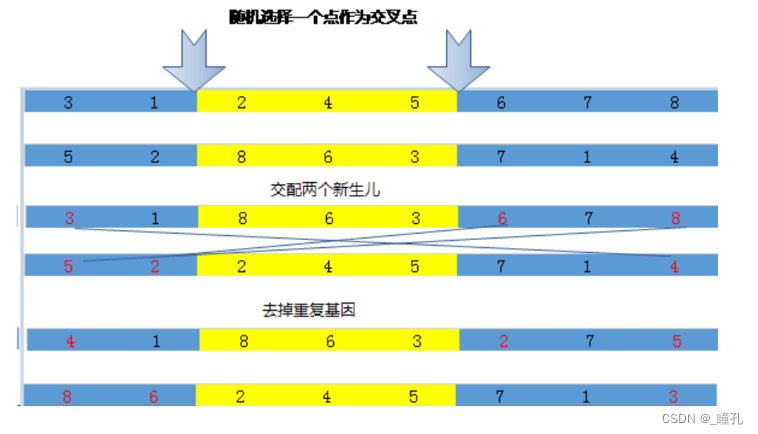
两点交叉运算：

突变（Mutation）：突变操作的目的是定期随机更新种群，将新模式引入染色体，并鼓励在解空间的未知区域中进行搜索。突变可能表现为基因的随机变化。变异是通过随机改变一个或多个染色体值来实现的。例如，翻转二进制串中的一位：

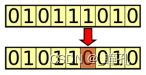
以下是一个遗传场景：

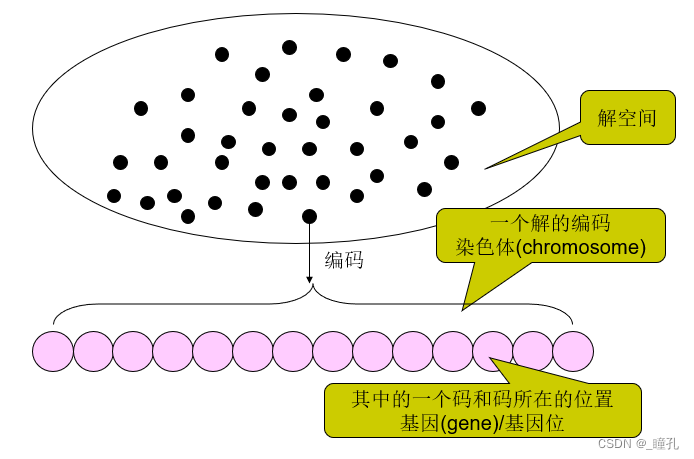
编解码过程图示：

编码策略评估：

• 完备性(completeness)：问题空间中的所有点(候选解)都能作为GA空间中的点(染色体)表现
• 健全性(soundness): GA空间中的染色体能对应所有问题空间中的候选解。
• 非冗余性(non-redundancy)：染色体和候选解一一对应。

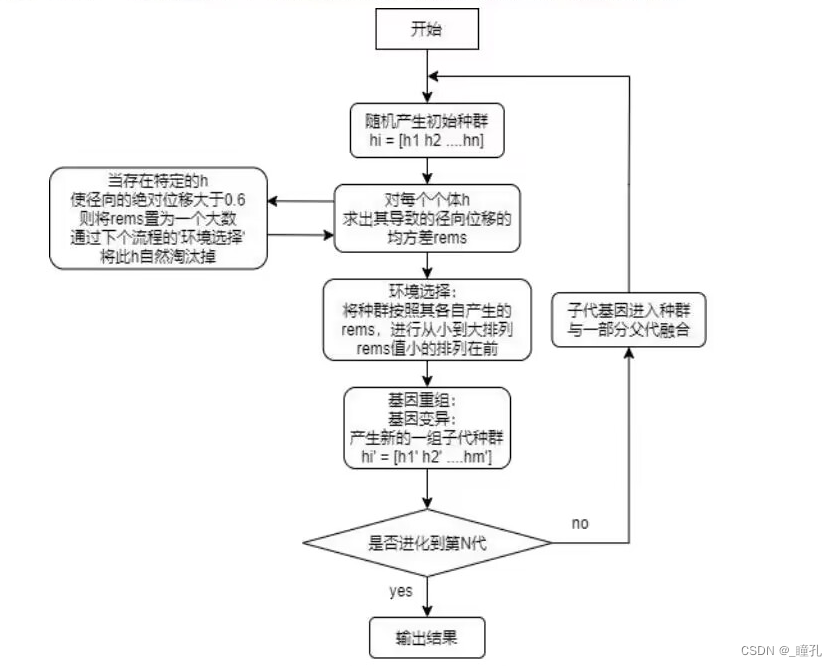
2.3：算法流程

遗传算法概念流程如下：

• 初始化。随机选择一些个体组成最初的种群(population)
• 评估函数。通过某种方法来评估个体的适应度，即衡量染色体（解）的优劣。
• 选择selection 。自然选择，优良的基因、生存能力强的被选择下来的概率要大。
• 交叉crossover。产生后代，基因交叉，可以理解为有性繁殖，子代会分别从父母那得到部分基因
• 变异mutation。后代的基因可能会变异。变异在生物进化起了很大作用

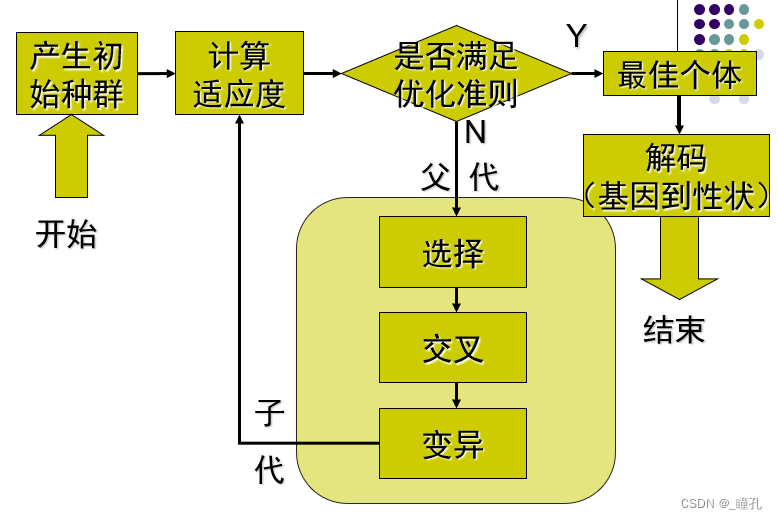
遗传算法步骤如下：

• 首先将变量二进制化，产生随机初始种群，并计算种群中每个个体的适应度值
• 按照适应度将种群个体进行排序，再依次执行基因重组与基因变异，得到子代新种群
• 将子代群体插入到父代群体中，筛选出适应度值优良的个体
• 进入到下一次的进化，直到进化到制定代数时停止并输出最优解

2.4：遗传算法总结

遗传算法应用：

• 函数优化：函数优化是遗传算法的经典应用领域，也是遗传算法进行性能评价的常用算例，如：连续函数和离散函数、凸函数和凹函数、低维函数和高维函数、单峰函数和多峰函数等。对于一些非线性、多模型、多目标的函数优化问题，用其它优化方法较难求解，而遗传算法可以方便的得到较好的结果。
• 组合优化：随着问题规模的增大，组合优化问题的搜索空间也急剧增大，有时在计算上用枚举法很难求出最优解。对这类复杂的问题，人们已经意识到应把主要精力放在寻求满意解上，而遗传算法是寻求这种满意解的最佳工具之一。实践证明，遗传算法对于组合优化中的NP问题非常有效。例如遗传算法已经在求解旅行商问题、背包问题、装箱问题、图形划分问题等方面得到成功的应用。
• 车间调度：车间调度问题是一个典型的NP-Hard问题，遗传算法作为一种经典的智能算法广泛用于车间调度中，很多学者都致力于用遗传算法解决车间调度问题，现今也取得了十分丰硕的成果。从最初的传统车间调度（JSP）问题到柔性作业车间调度问题（FJSP），遗传算法都有优异的表现，在很多算例中都得到了最优或近优解。
• 遗传算法也在生产调度问题、自动控制、机器人学、图象处理、人工生命、遗传编码和机器学习等方面获得了广泛的运用。

常规优化算法：

• 解析法：只能得到局部最优解，且要求目标函数连续光滑及可微信息
• 枚举法：虽然克服了这些缺点，但计算效率太低，且对于实际问题往往由于搜索空间大而不能将所有的情况都搜索到
• 动态规划法：存在“指数爆炸”问题，它对于中等规模和适度复杂性的问题，也常常无能为力

同常规算法相比，遗传算法有以下特点：

• 算法从问题解的集合（种群）开始搜索，而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的；容易误入局部最优解。
• 遗传算法同时处理群体中的多个个体，即对搜索空间中的多个解进行评估，覆盖面大，利于全局择优，减少了陷入局部最优解的风险，同时算法本身易于实现并行化。
• 遗传算法是对决策变量的编码进行操作，这样提供的参数信息量大，优化效果好。
• 遗传算法是从许多点开始并行操作，因而可以有效地防止搜索过程收敛于局部最优解。
• 遗传算法通过目标函数来计算适配值，而不需要其他推导和附加信息，从而对问题的依赖性小。
• 遗传算法的寻优规则是由概率决定的，而非确定性的。

遗传算法的优点

• 全局最优：在许多情况下，优化问题具有局部最大值和最小值。这些值代表的解比周围的解要好，但并不是最佳的解。大多数传统的搜索和优化算法，尤其是基于梯度的搜索和优化算法，很容易陷入局部最大值，而不是找到全局最大值。遗传算法更有可能找到全局最大值。这是由于使用了一组候选解，而不是一个候选解，而且在许多情况下，交叉和变异操作将导致候选解与之前的解有所不同。只要设法维持种群的多样性并避免过早趋同（premature convergence），就可能产生全局最优解。
• 处理复杂问题：由于遗传算法仅需要每个个体的适应度函数得分，而与适应度函数的其他方面（例如导数）无关，因此它们可用于解决具有复杂数学表示、难以或无法求导的函数问题。
• 处理缺乏数学表达的问题：遗传算法可用于完全缺乏数学表示的问题。这是由于适应度是人为设计的。例如，想要找到最有吸引力颜色组合，可以尝试不同的颜色组合，并要求用户评估这些组合的吸引力。使用基于意见的得分作为适应度函数应用遗传算法搜索最佳得分组合。即使适应度函数缺乏数学表示，并且无法直接从给定的颜色组合计算分数，但仍可以运行遗传算法。只要能够比较两个个体并确定其中哪个更好，遗传算法甚至可以处理无法获得每个个体适应度的情况。例如，利用机器学习算法在模拟比赛中驾驶汽车，然后利用基于遗传算法的搜索可以通过让机器学习算法的不同版本相互竞争来确定哪个版本更好，从而优化和调整机器学习算法。
• 耐噪音：一些问题中可能存在噪声现象。这意味着，即使对于相似的输入值，每次得到的输出值也可能有所不同。例如，当从传感器产生异常数据时，或者在得分基于人的观点的情况下，就会发生这种情况。尽管这种行为可以干扰许多传统的搜索算法，但是遗传算法通常对此具有鲁棒性，这要归功于反复交叉和重新评估个体的操作。
• 并行性：遗传算法非常适合并行化和分布式处理。适应度是针对每个个体独立计算的，这意味着可以同时评估种群中的所有个体。另外，选择、交叉和突变的操作可以分别在种群中的个体和个体对上同时进行。
• 持续学习：进化永无止境，随着环境条件的变化，种群逐渐适应它们。遗传算法可以在不断变化的环境中连续运行，并且可以在任何时间点获取和使用当前最佳的解。但是需要环境的变化速度相对于遗传算法的搜索速度慢。

遗传算法的局限性：

• 需要特殊定义：将遗传算法应用于给定问题时，需要为它们创建合适的表示形式——定义适应度函数和染色体结构，以及适用于该问题的选择、交叉和变异算子。
• 超参数调整：遗传算法的行为由一组超参数控制，例如种群大小和突变率等。将遗传算法应用于特定问题时，没有标准的超参数设定规则。
• 计算密集：种群规模较大时可能需要大量计算，在达到良好结果之前会非常耗时。可以通过选择超参数、并行处理以及在某些情况下缓存中间结果来缓解这些问题。
• 过早趋同：如果一个个体的适应能力比种群的其他个体的适应能力高得多，那么它的重复性可能足以覆盖整个种群。这可能导致遗传算法过早地陷入局部最大值，而不是找到全局最大值。为了防止这种情况的发生，需要保证物种的多样性。
• 无法保证的解的质量：遗传算法的使用并不能保证找到当前问题的全局最大值（但几乎所有的搜索和优化算法都存在此类问题，除非它是针对特定类型问题的解析解）。通常，遗传算法在适当使用时可以在合理的时间内提供良好的解决方案。