CRF条件随机场

1.HMM是生成式有向图模型（隐马尔可夫模型）

  MEMM是判别式有向图模型（最大熵模型）

  CRF是判别式无向图模型（条件随机场）

团： 无向图中任何两个节点均有边连接的节点子集。

最大团：最多有几个节点两两之间相互连接。

1/Z:归一化，缩放成概率；c:有几个最大团，累乘几项。Yc:最大团。

其中 t和s是特征函数，不是0就是1，t定义的是边上的特征函数，叫做转移特征，依赖于当前和前一个位置，s是定义在节点上的特征函数，称为状态特征，依赖于当前位置。

CRF：  1.无向图，依赖更多

            2.特征函数两类

            3.当团为3，把整个句子x作为了输入。

条件随机场有两类特征函数： 

            1.状态特征函数s

            2.转移特征函数t

在最大熵模型中，只是定义出来了某个中文字能不能被标成某种词性。而在crf模型中，除了定义出来上述关系之外，还定义出来，某个词性下一个词能不能被标记成某个词性。

极大似然估计和交叉熵是等价的。

极大似然估计：从概率的角度出发

交叉熵：从熵的角度出发（熵：反映一个物体的混乱程度。）

HMM,MEMM,CRF

相同点：都是做解码问题的。

CRF：

概率有向图又称为贝叶斯网络，概率无向图又称为马尔科夫网络。具体地，他们的核心差异表现在如何求  ，即怎么表示这个的联合概率。

一、概率有向图

对于有向图模型，这么求联合概率：

 

例如下图的联合概率表示如下：

 

 

二、概率无向图

 

如何求解其联合概率分布呢？

　　将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作。

团：无向图中任何两个节点均有边连接的节点子集。

最大团：若C为无向图G中的一个团，并且不能再加进任何一个G的节点时其成为一个更大的团，则称此团为最大团。上图中{Y2,Y3,Y4}和{Y1,Y3,Y4}都是最大团。

 概率无向图模型的联合概率分布P(Y)可以表示为如下形式：

 

 

其中t和s是特征函数，不是0就是1，t定义的是边上的特征函数，叫做转移特征，依赖于当前和前一个位置，s是定义在节点上的特征函数，称为状态特征，依赖于当前位置。

其中C是无向图最大团，Yc是C的节点对应的随机变量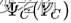， 是一个势函数，乘积是在无向图所有最大团上进行的，Z是归一化因子，保证P(Y)最后构成一个概率分布。

 

 CRF中的特征函数：

 

 三、条件随机场（conditional random field）

设X与Y是随机变量，P(Y|X)是给定X的条件下Y的条件概率分布，若随机变量Y构成一个由无向图G=(V,E)表示的马尔科夫随机场。则称条件概率分布P(Y|X)为条件随机场。因为是在X条件下的马尔科夫随机场，所有叫条件随机场。
虽然定义里面没有要求，我们还是默认X和Y结构一致，这是general CRF。然后看看linear chain CRF，线性链就是X和Y都是一串序列。

 linear chain CRF的公式如下：

 

再详细一些如下：

 

t和s都是特征函数，一个是转移特征，一个状态特征，x=（x1,x2,...,xn）为观察变量,y=(y1,y2,...,yn)为隐含变量。所以，CRF也就是直接预测p（y|x）,属于判别式模型。注意一个细节，特征函数里面的观测变量为x，而不是xi，这也就是说你可以前后随意看观测变量，所以特征模板里面可以随意定义前后要看几个观测值。

亦或表示如下：

 

O为观察序列，I为预测的隐变量序列。

四、模型训练与运行

1）训练

CRF模型的训练主要训练特征函数的权重参数λ，一般情况下不把两种特征区别的那么开，合在一起如下：

 

每个token会对应多个特征函数，特征函数f取值为0或者1，在训练的时候主要训练权重λ，权重为0则没贡献，甚至你还可以让他打负分，充分惩罚。利用极大似然估计寻找最优参数解。

2）工作流程

模型的工作流程：

step1. 先预定义特征函数 

 

step2. 在给定的数据上，训练模型，确定参数

 

step3. 用确定的模型做序列标注问题或者序列求概率问题

3）序列标注

还是跟HMM一样的，用学习好的CRF模型，在新的sample（观测序列 O1.......Oi）上找出一条概率最大最可能的隐状态序列i1.....ii。

只是现在的图中的每个隐状态节点的概率求法有一些差异而已,正确将每个节点的概率表示清楚，路径求解过程还是一样，采用viterbi算法

HMM

HMM是最早提出来的动机是为了类似解决序列标注问题的一个理想模型，也是一个基于P(X|Y)建模的概率生成模型。之所以说理想，是因为它的核心思想是建立在两个假设上面：

• 一阶齐次马尔可夫假设
• 观测独立假设

显然这两个假设都是离实际偏差比较大，因此它的优缺点和适用场景也很明显：

优点：

有了这两个假设，假设成立的场景，可以大大简化概率P(X|Y)的计算。

缺点：

不适用于一般场景，应用范围比较窄。

因为是生成模型，因为不是判别标注类别，不如概率判别模型计算量小。

MEMM

MEMM是最大熵马尔可夫模型，向较于HMM，它出现的动机主要是打破了HMM的观测独立假设，拓宽了实际应用的场景范围。同时，它还是一个基于P(Y|X)的概率判别模型。
所以它的核心思想是：改造HMM，打破HMM的观测独立假设。
它的优缺点和适用场景也是相对于HMM来说：

优点：

没有观测独立假设，很明显它比HMM有更宽的适用场景

因为是概率判别模型，直接对P(Y|X)计算，不需要算联合概率等中间步骤，计算量小。

缺点：

MEMM有一个致命的问题，即标注偏差问题，导致这个问题的原因是局部归一化，因为这个问题,限制了它的实际使用，实际用途不大。

CRF

CRF的出现是建立在MEMM之上，因为MEMM存在标注偏差问题，所以CRF的动机就是为了解决这个问题，这也是它的核心思想，具体实现是把Y的有向状态转移改成无向。和MEMM一样，CRF也是一个概率判别模型。
它的优缺点和适用场景也是相对于MEMM和HMM而言：

优点：

相比于MEMM的Y的有向状态转移，CRF的无向状态转移，打破了HMM的齐次假设，使CRF的适用场景更宽。

同时，基于无向的状态转移，是天然的全局归一化，不存在局部归一化问题，CRF解决了MEMM的序列标注问题

CRF是无向图因此它的Y可以向各个方向转移

缺点：

网上说训练代价大、复杂度高；这个也是相对的，相对于MEMM，CRF是全局归一化，需要计算整个标记序列的联合概率分布，其采用基于动态规划的维特比算法达到全局最优标注。