• VTK网格细分-vtkAdaptiveSubdivisionFilter

    欢迎大家加入社区，雪易VTK社区-CSDN社区云

    前言：此博文主要分享VTK中关于细分网格的相关Filter，同时希望能给其他小伙伴一些帮助。

    小结：VTK中关于网格细分的Filter包括vtkSubdivisionFilter和vtkAdaptiveSubdivisionFilter。其中vtkSubdivisionFilter又有几个子类，见下图。

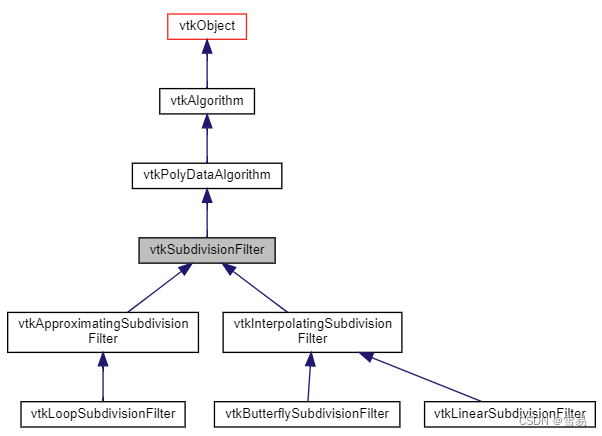
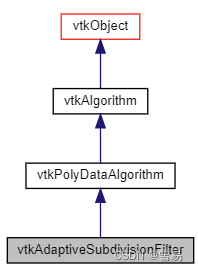
    现以正方形为例展示各个细分Filter的不同之处（所有的numberOfSubdivision设为2），原始模型为下图：

      

    1. vtkAdaptiveSubdivisionFilter 

     描述：vtkAdaptiveSubdivisionFilter是基于三角形的最长边或面积进行细分的Filter。新增的点只能插入到边缘上，根据细分的边的数量，插入不同数量的三角形，范围从两个（即两个三角形取代原来的一个）到四个。

    参数：

    1. MaximumEdgeLength：指定最长边的长度。若长度大于当前设定值，则将其进行剖分。

    2. MaximunTriangleArea：指定三角面片的最大面积，若面积大于当前设定值，则进行剖分。若使用这个标准，结果可能会产生non-watertight网格。

    算法实现过程：

    1. 初始化MaximunEdgeLength = 1.0; MaximunTriangleArea = 1.0;

    2. 八种细分方案

    1. // There are eight possible subdivision cases (each of the three edges may
    2. // or may not be subdivided). Case 0 just outputs the original triangle;
    3. // the other cases output between 2 and four triangles. Note that when
    4. // three triangles are generated, then the diagonal of the quadrilateral
    5. // produced can go one of two ways. The tetCases is set up so that the two
    6. // triangles forming the quad are the last two triangles and can be
    7. // adjusted as necessary.
    8. int CASE_MASK[3] = { 1, 2, 4 };
    9. vtkIdType tessCases[16][13] = {
    10.   { 1, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0 }, // case 0
    11.   { 2, 0, 3, 2, 3, 1, 2, 0, 0, 0, 0, 0, 0 }, // case 1
    12.   { 2, 0, 1, 4, 4, 2, 0, 0, 0, 0, 0, 0, 0 }, // case 2
    13.   { 3, 3, 1, 4, 3, 4, 2, 2, 0, 3, 0, 0, 0 }, // case 3
    14.   { 2, 0, 1, 5, 5, 1, 2, 0, 0, 0, 0, 0, 0 }, // case 4
    15.   { 3, 0, 3, 5, 5, 3, 1, 1, 2, 5, 0, 0, 0 }, // case 5
    16.   { 3, 5, 4, 2, 0, 1, 4, 4, 5, 0, 0, 0, 0 }, // case 6
    17.   { 4, 0, 3, 5, 3, 1, 4, 5, 3, 4, 5, 4, 2 }, // case 7
    18.   { 1, 0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0 }, // case 0a
    19.   { 2, 0, 3, 2, 3, 1, 2, 0, 0, 0, 0, 0, 0 }, // case 1a
    20.   { 2, 0, 1, 4, 4, 2, 0, 0, 0, 0, 0, 0, 0 }, // case 2a
    21.   { 3, 3, 1, 4, 0, 3, 4, 4, 2, 0, 0, 0, 0 }, // case 3a
    22.   { 2, 0, 1, 5, 5, 1, 2, 0, 0, 0, 0, 0, 0 }, // case 4a
    23.   { 3, 0, 3, 5, 3, 1, 2, 2, 5, 3, 0, 0, 0 }, // case 5a
    24.   { 3, 4, 2, 5, 5, 0, 1, 1, 4, 5, 0, 0, 0 }, // case 6a
    25.   { 4, 0, 3, 5, 3, 1, 4, 5, 3, 4, 5, 4, 2 }, // case 7a
    26. };

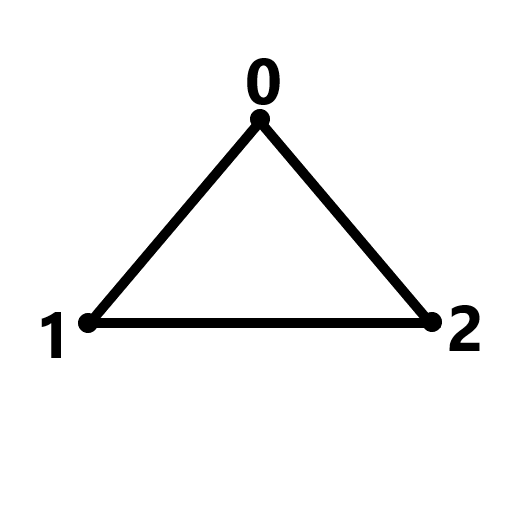
     （case0，case0a）

     

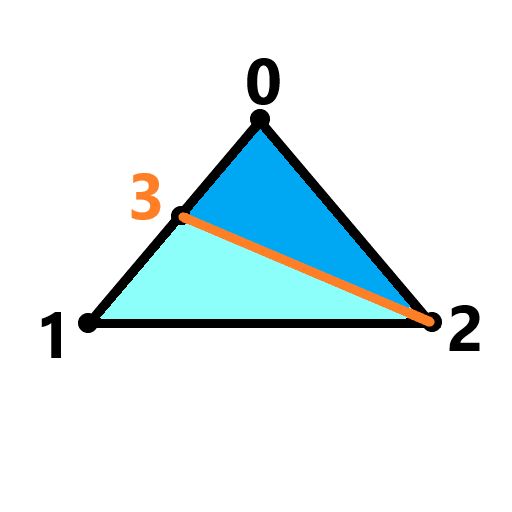
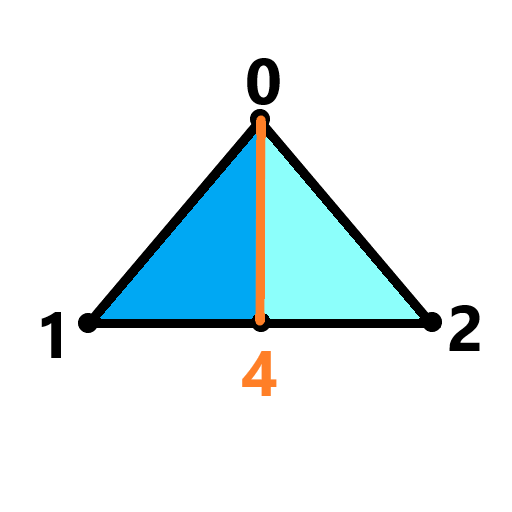
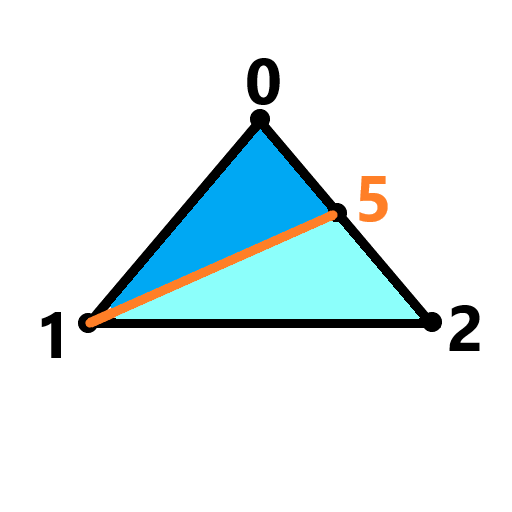
     （case1，case1a）         （case2，case2a）         （case4，case4a）

     

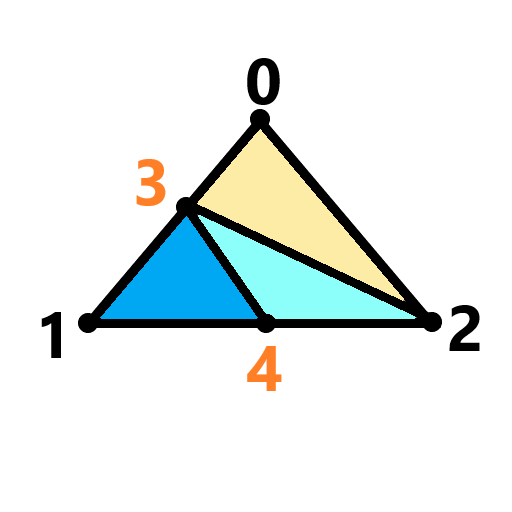
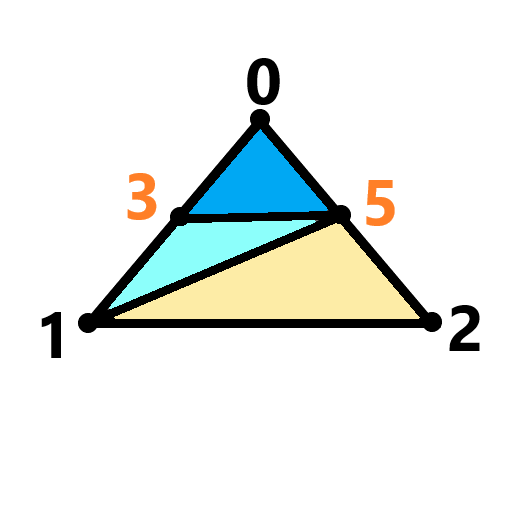
                 (case3)                          (case5)                            (case6) 

     

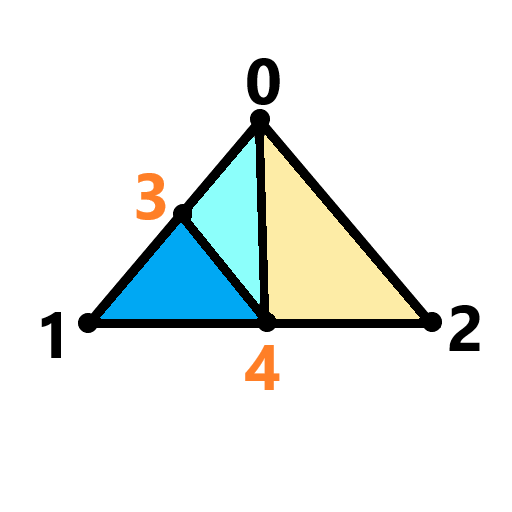
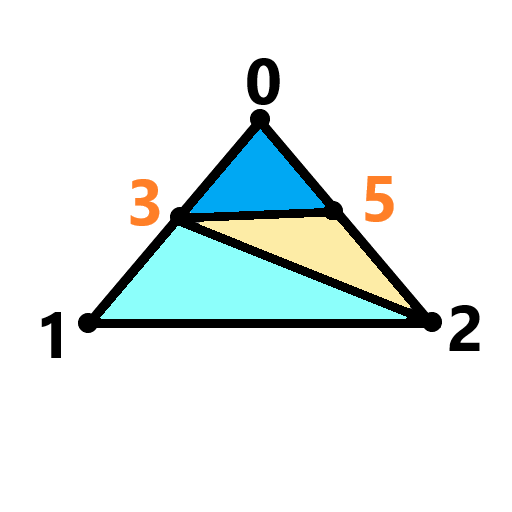
                  (case3a)                          (case5a)                            (case6a) 

     

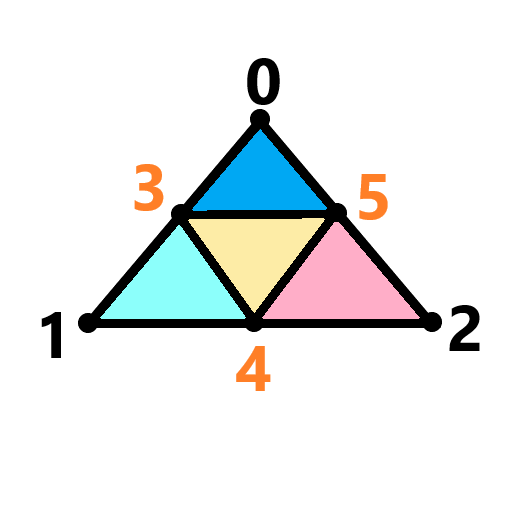
     （case7，case7a） 
     

    3. 细分逻辑

      若三角面片的面积 > 指定最大面积，则采用case7进行分类；

      若仅有直线01的长度 > 指定最大长度，则采用case1进行分类；

      若仅有直线12的长度 > 指定最大长度，则采用case2进行分类；

      若仅有直线20的长度 > 指定最大长度，则采用case4进行分类；

      若直线01的长度 > 指定最大长度 && 直线12的长度 > 指定最大长度，则采用case3进行分类；

      若直线01的长度 > 指定最大长度 && 直线20的长度 > 指定最大长度，则采用case5进行分类；

      若直线12的长度 > 指定最大长度 && 直线20的长度 > 指定最大长度，则采用case6进行分类；

      针对case3,case5,case6的分类，再比较case3和case3a，case5和case5a，case6和case6a，选择最优剖分方式。

    小结：设定的面积值是由于长度值的。

    1. int vtkAdaptiveSubdivisionFilter::RequestData(vtkInformation* vtkNotUsed(request),
    2.   vtkInformationVector** inputVector, vtkInformationVector* outputVector)
    3. {
    4.   // get the info objects
    5.   vtkInformation* inInfo = inputVector[0]->GetInformationObject(0);
    6.   vtkInformation* outInfo = outputVector->GetInformationObject(0);
    7.  
    8.   // get the input and output and check its validity
    9.   vtkPolyData* input = vtkPolyData::SafeDownCast(inInfo->Get(vtkDataObject::DATA_OBJECT()));
    10.   vtkPolyData* output = vtkPolyData::SafeDownCast(outInfo->Get(vtkDataObject::DATA_OBJECT()));
    11.  
    12.   vtkIdType numPts = input->GetNumberOfPoints();
    13.   vtkCellArray* inTris = input->GetPolys();
    14.   vtkIdType numTris = inTris->GetNumberOfCells();
    15.   if (numPts < 1 || numTris < 1)
    16.   {
    17.     vtkDebugMacro(<< "No data to subdivide!");
    18.     return 1;
    19.   }
    20.   vtkPointData* inPointData = input->GetPointData();
    21.   vtkCellData* inCellData = input->GetCellData();
    22.  
    23.   if (inTris->IsHomogeneous() != 3)
    24.   {
    25.     vtkDebugMacro(<< "Filter operates only on triangles!");
    26.     return 1;
    27.   }
    28.  
    29.   // Need a locator
    30.   if (!this->Locator)
    31.   {
    32.     this->CreateDefaultLocator();
    33.   }
    34.  
    35.   // The first thing is to take the existing points and push them into the
    36.   // incremental point locator. We know that we are going to use the original
    37.   // points. Note that points are only created and are not swapped as each
    38.   // pass is invoked.
    39.   vtkPoints* inPts = input->GetPoints();
    40.   vtkPoints* newPts = vtkPoints::New();
    41.   vtkPointData *swapPointData, *newPointData = vtkPointData::New();
    42.   newPointData->CopyAllocate(inPointData);
    43.  
    44.   // set precision for the points in the output
    45.   if (this->OutputPointsPrecision == vtkAlgorithm::DEFAULT_PRECISION)
    46.   {
    47.     newPts->SetDataType(inPts->GetDataType());
    48.   }
    49.   else if (this->OutputPointsPrecision == vtkAlgorithm::SINGLE_PRECISION)
    50.   {
    51.     newPts->SetDataType(VTK_FLOAT);
    52.   }
    53.   else if (this->OutputPointsPrecision == vtkAlgorithm::DOUBLE_PRECISION)
    54.   {
    55.     newPts->SetDataType(VTK_DOUBLE);
    56.   }
    57.   this->Locator->InitPointInsertion(newPts, input->GetBounds(), input->GetNumberOfPoints());
    58.   // Load in the already existing points. Also load in the point data
    59.   // associated with the existing points.
    60.   for (vtkIdType ptId = 0; ptId < numPts; ++ptId)
    61.   {
    62.     this->Locator->InsertNextPoint(inPts->GetPoint(ptId));
    63.     newPointData->CopyData(inPointData, ptId, ptId);
    64.   }
    65.  
    66.   // This is a multipass algorithm. From a list of triangles, check each
    67.   // against the edge length and area criteria. If necessary, break the
    68.   // triangle (using a case table) into smaller triangles by inserting one or
    69.   // more points on edges (the edge is broken at its midpoint). The new
    70.   // triangles are placed into a new list which serves as the starting point
    71.   // for the next pass. An important note: triangles are split independently
    72.   // without neighbor "links" (i.e.,cell links) and new points are merged
    73.   // into the locator. Since the algorithm treats edges on triangles in an
    74.   // identical way, the end result is that triangle neighbors remain
    75.   // compatible (due to conincident point merging).
    76.   //这是一个多通道算法。从三角形列表中，根据边长和面积标准检查每个三角形。如果有必要，通过在边缘  
    77.   //上插入一个或多个点(边缘在中点被打破)，将三角形(使用案例表)分割成更小的三角形。
    78.   //新的三角形被放置到一个新的列表中，作为下一遍的起点。
    79.   //一个重要的注意事项:三角形是独立分割的，没有相邻的“链接”(即单元格链接)，新的点被合并到定位器  
    80.   //中。由于该算法以相同的方式处理三角形上的边，最终结果是三角形邻居保持兼容(由于重合点合并)。
    81.   auto cellIter = vtk::TakeSmartPointer(inTris->NewIterator());
    82.   vtkCellArray *swapTris, *newTris = vtkCellArray::New();
    83.   newTris->AllocateEstimate(2 * numTris, 3);
    84.   vtkCellData *swapCellData, *newCellData = vtkCellData::New();
    85.   newCellData->CopyAllocate(inCellData);
    86.  
    87.   int i;
    88.   double area, eLengths[3];
    89.   double maxLen2 = this->MaximumEdgeLength * this->MaximumEdgeLength;
    90.   double maxArea = this->MaximumTriangleArea;
    91.   double x[6][3]; // three vertices plus potential mid-edge points
    92.   const vtkIdType* tri;
    93.   vtkIdType triId;
    94.   vtkIdType newId;
    95.   vtkIdType passNum;
    96.   vtkIdType totalTriangles = 0;
    97.   bool changesMade;
    98.  
    99.   for (passNum = 0, changesMade = true; passNum < this->MaximumNumberOfPasses &&
    100.        totalTriangles < this->MaximumNumberOfTriangles && changesMade;
    101.        ++passNum)
    102.   {
    103.     changesMade = false;
    104.     for (cellIter->GoToFirstCell(); !cellIter->IsDoneWithTraversal(); cellIter->GoToNextCell())
    105.     {
    106.       triId = cellIter->GetCurrentCellId();
    107.       {
    108.         vtkIdType unused;
    109.         cellIter->GetCurrentCell(unused, tri);
    110.       }
    111.  
    112.       newPts->GetPoint(tri[0], x[0]);
    113.       newPts->GetPoint(tri[1], x[1]);
    114.       newPts->GetPoint(tri[2], x[2]);
    115.       eLengths[0] = vtkMath::Distance2BetweenPoints(x[0], x[1]);
    116.       eLengths[1] = vtkMath::Distance2BetweenPoints(x[1], x[2]);
    117.       eLengths[2] = vtkMath::Distance2BetweenPoints(x[2], x[0]);
    118.       area = vtkTriangle::TriangleArea(x[0], x[1], x[2]);
    119.  
    120.       // Various subdivision cases are possible
    121.       unsigned char subCase = 0;
    122.       if (area > maxArea)
    123.       {
    124.         subCase = 7;
    125.       }
    126.       else
    127.       {
    128.         for (i = 0; i < 3; ++i)
    129.         {
    130.           if (eLengths[i] > maxLen2)
    131.           {
    132.             subCase |= CASE_MASK[i];
    133.           }
    134.         }
    135.       } // determine edges to divide
    136.  
    137.       // If not just outputting original triangle then changes are made
    138.       if (subCase > 0)
    139.       {
    140.         changesMade = true;
    141.       }
    142.  
    143.       // Now create new points and triangles dividing edges as appropriate.
    144.       double xNew[3];
    145.       vtkIdType ptIds[6];
    146.       ptIds[0] = tri[0];
    147.       ptIds[1] = tri[1];
    148.       ptIds[2] = tri[2];
    149.       for (i = 0; i < 3; ++i)
    150.       {
    151.         if (subCase & CASE_MASK[i]) // ith edge needs subdivision
    152.         {
    153.           xNew[0] = 0.5 * (x[i][0] + x[(i + 1) % 3][0]);
    154.           xNew[1] = 0.5 * (x[i][1] + x[(i + 1) % 3][1]);
    155.           xNew[2] = 0.5 * (x[i][2] + x[(i + 1) % 3][2]);
    156.           if ((ptIds[3 + i] = this->Locator->IsInsertedPoint(xNew)) < 0)
    157.           {
    158.             ptIds[3 + i] = this->Locator->InsertNextPoint(xNew);
    159.             newPointData->InterpolateEdge(inPointData, ptIds[3 + i], tri[i], tri[(i + 1) % 3], 0.5);
    160.           }
    161.         }
    162.       }
    163.  
    164.       // The tessellation may vary based on geometric concerns (selecting best
    165.       // diagonal during triangulation of quadrilateral)
    166.       vtkIdType newTIds[3], *subTess;
    167.       subTess = SelectTessellation(subCase, ptIds, newPts);
    168.       vtkIdType numTessTris = *subTess++;
    169.  
    170.       for (i = 0; i < numTessTris; ++i, subTess += 3)
    171.       {
    172.         newTIds[0] = ptIds[subTess[0]];
    173.         newTIds[1] = ptIds[subTess[1]];
    174.         newTIds[2] = ptIds[subTess[2]];
    175.         newId = newTris->InsertNextCell(3, newTIds);
    176.         newCellData->CopyData(inCellData, triId, newId);
    177.         if (++totalTriangles >= this->MaximumNumberOfTriangles)
    178.         {
    179.           break;
    180.         }
    181.       }
    182.     } // for all triangles in this pass
    183.  
    184.     // Prepare for the next pass, which means swapping input and output.
    185.     // Remember that the initial pass uses the filter input; subsequent passes
    186.     // cannot modify the input to a new cell array must be created to support
    187.     // the swapping.
    188.     if (passNum == 0)
    189.     {
    190.       inTris = vtkCellArray::New();
    191.       inCellData = vtkCellData::New();
    192.       inCellData->CopyAllocate(newCellData);
    193.  
    194.       inPointData = vtkPointData::New();
    195.       inPointData->CopyAllocate(newPointData);
    196.     }
    197.  
    198.     // Prepare for new triangles
    199.     swapTris = newTris;
    200.     newTris = inTris;
    201.     inTris = swapTris;
    202.     cellIter = vtk::TakeSmartPointer(inTris->NewIterator());
    203.  
    204.     numTris = inTris->GetNumberOfCells();
    205.     newTris->Reset();
    206.     newTris->AllocateEstimate(2 * numTris, 3);
    207.  
    208.     // Prepare for new cell data
    209.     swapCellData = newCellData;
    210.     newCellData = inCellData;
    211.     inCellData = swapCellData;
    212.  
    213.     // Prepare for new point data
    214.     numPts = newPts->GetNumberOfPoints();
    215.     swapPointData = newPointData;
    216.     newPointData = inPointData;
    217.     inPointData = swapPointData;
    218.     for (vtkIdType ptId = 0; ptId < numPts; ++ptId)
    219.     {
    220.       newPointData->CopyData(inPointData, ptId, ptId);
    221.     }
    222.   } // for another pass
    223.  
    224.   // Configure output and clean up
    225.   output->SetPoints(newPts);
    226.   newPts->Delete();
    227.   output->GetPointData()->ShallowCopy(inPointData);
    228.   newPointData->Delete();
    229.  
    230.   output->SetPolys(inTris);
    231.   inTris->Delete();
    232.   newTris->Delete();
    233.   output->GetCellData()->ShallowCopy(inCellData);
    234.   inCellData->Delete();
    235.   inPointData->Delete();
    236.   newCellData->Delete();
    237.  
    238.   return 1;
    239. }

    2. vtkLoopSubdivisionFilter

    描述：vtkLoopSubdivisionFilter是一个近似细分的子类，它为网格中的每个三角形创建四个新的三角形。

    算法实现原理：

    1)  GenerateSubdivisionPoints:生成细分的点

    for (针对输入PolyData的所有Point)

    {

            a. 获取当前点关联的其它点，并确认关联点的比重；

            b. 根据关联点的坐标和各自的比重计算当前点的新的坐标；

            c. 将新的点集更新至输出PolyData。

    }

    2）将细分出的新增点连接生成Cell

    3. vtkButterflySubdivisionFilter

    描述：vtkButterflySubdivisionFilter是一个插值细分的子类，它采用蝴蝶细分的方法为网格中的每个三角形创建四个新的三角形。

    4. vtkLinearSubdivisionFilter

    描述：vtkLinearSubdivisionFilter是一个插值细分的子类，同样为网格中的每个三角形创建四个新的三角形。

  • 相关阅读:
    Android 使用 TextView 显示网页内容
    Docker 介绍
    longjmp导致局部变量丢失
    LLM-TAP随笔——语言模型训练数据【深度学习】【PyTorch】【LLM】
    LabVIEW异步调用VI
    直流有刷电机驱动基于STM32F302R8+X-NUCLEO-IHM07M1（二）
    问题（05）elementui 输入框里面禁止浏览器自动填充用户名密码、弹出浏览器历史密码提示框
    FDMA 3.1 米联客的Axi-DDR3控制器及其配套的Dbuf
    工具 - markdown编辑器常用方法
    JSP企业客户管理系统myeclipse定制开发mysql数据库网页模式java编程jdbc
  • 原文地址：https://blog.csdn.net/qq_40041064/article/details/128118621