Python快速计算24点游戏并获取表达式

24 点游戏规则

有4个范围在 [1,9] 的数字，通过「加、减、乘、除」四则运算能够获得24，认为有解。

4个范围在 [1,9] 的数字能够产生495种可能，其中404中组合情况都是有解的，有解概率高达81.62%。

下面我们用python来验证它，首先计算组合数：

from scipy.special import comb

comb(9, 4, repetition=True)
1
2
3

495.0
1

可以看到python计算出9个数字有重复的组合情况数是495。

下面我们需要一个方法，判断4个数字能否组合成为24点，这里我采用回溯算法进行计算。

回溯算法计算思路

首先从4个数字中选择2个数字，然后再选择一种运算操作，然后用得到的结果取代选出的2个数字。然后在剩下的3个数字中，进行同样的操作。依次类推，最终计算到只剩一个数字，看结果是否为24即可。

开始编码：

from operator import add, mul, sub, truediv
from itertools import permutations, combinations_with_replacement

ops = [add, mul, sub, truediv]


def judgePoint24(nums) -> bool:
    if not nums:
        return False
    n = len(nums)
    if n == 1:
        return round(nums[0], 3) == 24
    for i, j in permutations(range(n), 2):
        # 选2个数字
        x, y = nums[i], nums[j]
        # 选择加减乘除 4 种运算操作之一，用得到的结果取代选出的 2 个数字
        # 先添加未选择的数字
        newNums = [z for k, z in enumerate(nums) if k not in (i, j)]
        for k in range(4):
            if k < 2 and i > j:
                # 加法和乘法满足交换律,跳过第二种顺序
                continue
            if k == 3 and round(y, 3) == 0:
                # 除法运算除数不能为0
                continue
            newNums.append(ops[k](x, y))
            if judgePoint24(newNums):
                return True
            newNums.pop()
    return False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

然后我们遍历所有的组合进行判断：

from scipy.special import comb

total = int(comb(9, 4, repetition=True))
cnt = sum(judgePoint24(nums)
          for nums in combinations_with_replacement(range(1, 10), 4))
print(f'{cnt}/{total}={cnt/total:.2%}')
1
2
3
4
5
6

最终一秒内计算出结果：

生成表达式

下面我们加大难度，要求在求解时，能够同时返回可行的表达式。暴力遍历固然可以实现，但是耗时太长，能否在这种回溯算法的基础上实现呢？

我的思路是加个变量记录每次的选择，最终再通过一定的技巧进行还原，最终编码：

from operator import add, mul, sub, truediv
from itertools import permutations, combinations_with_replacement
from collections import defaultdict


def judgePoint24(nums) -> bool:
    ops = [add, mul, sub, truediv]
    op_char = "+*-/"
    record = []

    def solve(nums) -> bool:
        if not nums:
            return False
        n = len(nums)
        if n == 1:
            return round(nums[0], 3) == 24
        for i, j in permutations(range(n), 2):
            # 选2个数字
            x, y = nums[i], nums[j]
            newNums = []
            # 选择加减乘除 4 种运算操作之一，用得到的结果取代选出的 2 个数字
            # 先添加未选择的数字
            newNums = [z for k, z in enumerate(nums) if k not in (i, j)]
            for k in range(4):
                if k < 2 and i > j:
                    # 加法和乘法满足交换律,跳过第二种顺序
                    continue
                if k == 3 and round(y, 3) == 0:
                    # 除法运算除数不能为0
                    continue
                v = ops[k](x, y)
                newNums.append(v)
                record.append(([x, y], op_char[k], v))
                if solve(newNums):
                    return True
                newNums.pop()
                record.pop()
        return False
    flag = solve(nums)
    if not flag:
        return False, ""
    cache = defaultdict(list)
    for ns, op, v in record:
        for i in range(2):
            if cache[ns[i]]:
                ns[i] = "("+cache[ns[i]].pop()+")"
        r = f"{ns[0]}{op}{ns[1]}"
        cache[v].append(r)
    return flag, r+"=24"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

然后开始遍历：

total = cnt = 0
for nums in combinations_with_replacement(range(1, 10), 4):
    total += 1
    r, expression = judgePoint24(nums)
    if r:
        print(expression, end="\t")
        cnt += 1
        if cnt % 8 == 0:
            print()
print()
print(f'{cnt}/{total}={cnt/total:.2%}')
1
2
3
4
5
6
7
8
9
10
11

最终结果：

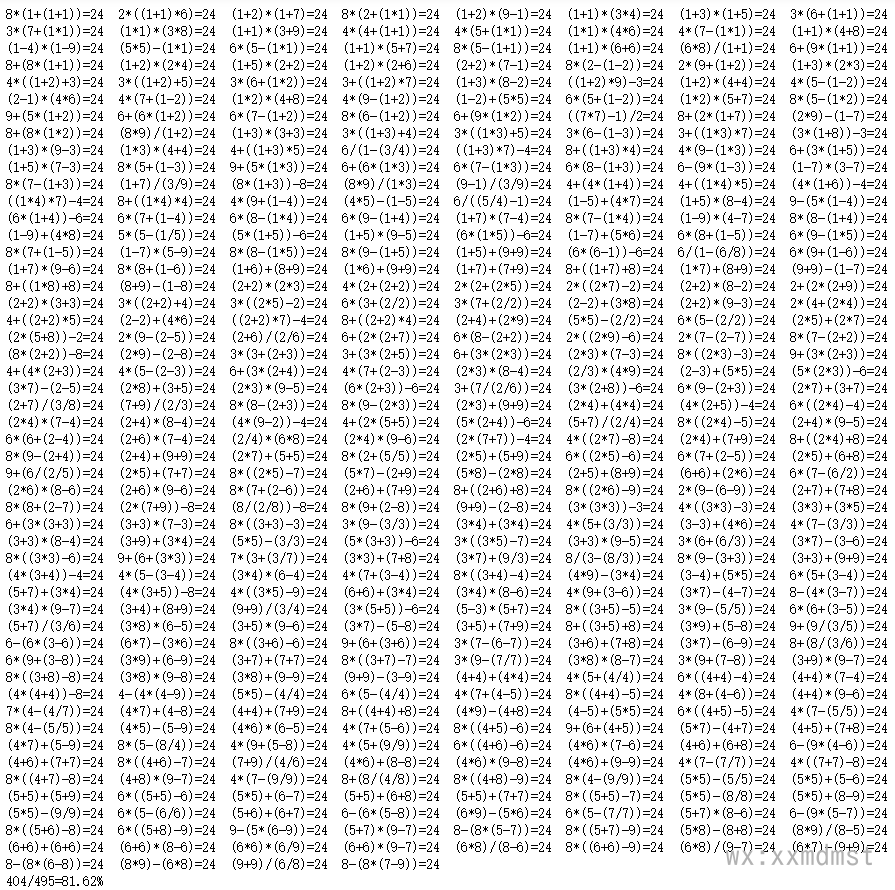
可以看到，我们已经得到了404个24点的有效解表达式。